Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
고급 벡터 연산¶
평면¶
외적은 단위 벡터에 대한 또 다른 흥미로운 속성을 갖고있습니다. 벡터에 수직이고 (원점을 통해) 평면을 통과한다고 상상해보십시오. 평면은 전체 공간을 양(비행기 위)과 음(비행기 아래)으로 나누면, (일반적으로 믿는 것과 무관) 그 연산들을 2차원에서도 사용할 수 있습니다:
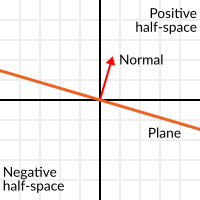
표면에 수직인 단위 벡터(표면의 방향을 서술합니다)를 단위 법선 벡터라고 합니다. 그러나 일반적으로 법선 벡터로 줄여 씁니다. 법선 벡터는 평면, 3차원 기하학(각 면 또는 정점이 어디서 마주보는지 결정하기 위해) 등에 나타납니다. 법선 벡터는 단위 벡터이지만, 이것의 사용법 때문에 법선 벡터 라고 합니다(원점을 (0,0)이라고 부르는 것처럼!).
The plane passes by the origin and the surface of it is perpendicular to the unit vector (or normal). The side towards the vector points to is the positive half-space, while the other side is the negative half-space. In 3D this is exactly the same, except that the plane is an infinite surface (imagine an infinite, flat sheet of paper that you can orient and is pinned to the origin) instead of a line.
평면과의 거리¶
이제 평면이 무엇인지 알았으니, 다시 내적으로 돌아가 봅시다. 단위벡터 와 공간 내 모든 점 사이의 내적 (예, 이번에는 벡터와 위치 간에 내적을수행함)은 점에서 평면까지의 거리를 반환합니다 :
var distance = normal.dot(point)
var distance = normal.Dot(point);
그러나 절대적인 거리가 아니라, 만약 점이 음수인 경우에는 거리도 음수입니다:
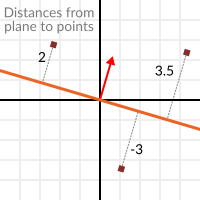
이것은 우리가 평면의 어느 쪽을 가리키는 것을 허락한다.
원점으로부터 멀리¶
난 당신이 무슨 생각을 하는지 압니다! 지금까지 이것은 좋았지만, 실제 평면은 원점만 통과하는 것이 아니라 공간 어디에나 있습니다. 실제 평면 작업을 원하는 경우 지금.
평면은 공간을 둘로 나눌 뿐만 아니라 극성 도 가지고 있다는 것을 기억하세요. 이는 완벽하게 겹치는 평면을 가질 수 있지만, 음의 면과 양의 면은 서로 교환된다는 것을 의미합니다.
이를 위해 전체 평면을 법선벡터 N 과 원점으로부터 스칼라 *D* 의 거리로 설명하겠습니다. 따라서 우리 평면은 N과 D로 보여집니다. 예를 들면 다음과 같습니다:
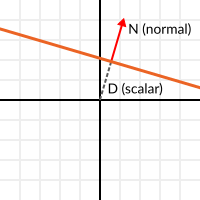
3차원 수학에서 Godot은 이를 처리하는 Plane 의 내장 유형을 제공합니다.
기본적으로 N과 D는 공간의 평면을 나타낼 수 있으며(N의 크기에 따라 다름) 2차원 또는 3차원의 경우 모두 수학이 동일합니다. 이전과 동일하지만, D는 원점에서부터 평면까지 N 방향으로 이동하는 거리입니다. 예를 들어, 평면의 한 지점에 도달하고 싶다고 가정해 보십시오:
var point_in_plane = N*D
var pointInPlane = N * D;
이것은 법선 벡터를 늘려 그것이 평면에 닿게 할 것입니다. 이 수학은 혼란스러워 보일지 모르지만 실제로는 보이는 것보다 훨씬 더 간단합니다. 만약 우리가 다시 한 번 점에서부터 평면까지의 거리를 알려고 한다면, 우리는 거리에 따라 조정만 하면 됩니다:
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
이것도 마찬가지로, 내장 함수 사용:
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
이것은 또 양수나 음수의 거리를 반환할 것입니다.
평면의 극성 N과 D를 모두 부정함으로써 뒤집을 수 있습니다. 이렇게 하면 평면이 동일한 위치에 있지만 반전된 음과 양의 절반 공간이 있는 평면이 됩니다:
N = -N
D = -D
N = -N;
D = -D;
Godot also implements this operator in Plane. So, using the format below will work as expected:
var inverted_plane = -plane
var invertedPlane = -plane;
So, remember, the plane's main practical use is that we can calculate the distance to it. So, when is it useful to calculate the distance from a point to a plane? Let's see some examples.
2D로 평면 구성하기¶
평면이 갑자기 나오지 않는 게 분명하니까 꼭 만들어져야합니다. 2D로 구성하는 것은 쉽습니다. 이것은 법선(단위 벡터)와 점 또는 공간의 두 점으로부터 수행될 수 있습니다.
In the case of a normal and a point, most of the work is done, as the normal is already computed, so calculate D from the dot product of the normal and the point.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
평면에서의 두 점은, 실제로 두 개의 평면이 그들을 통과하면서 같은 공간을 공유하지만, 법선 벡터는 보통 다른 방향을 가리킨다. 두 점에서 법선벡터를 계산하려면 먼저 방향 벡터를 얻은 다음 어느 쪽으로든 90° 회전해야 합니다:
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
The rest is the same as the previous example. Either point_a or point_b will work, as they are in the same plane:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Doing the same in 3D is a little more complex and is explained further down.
평면의 예¶
Here is an example of what planes are useful for. Imagine you have a convex polygon. For example, a rectangle, a trapezoid, a triangle, or just any polygon where no faces bend inwards.
폴리곤의 모든 세그먼트에 대해 해당 세그먼트를 통과하는 평면을 계산합니다. 평면 목록이 있으면 폴리곤 내부에 점이 있는지 확인하는 등 깔끔한 작업을 수행할 수 있습니다.
우리는 모든 평면을 통과합니다, 점까지의 거리가 양수인 평면을 찾을 수 있으면 점은 폴리곤 외부에 있습니다. 아니면 점은 폴리곤 내부에 있습니다.
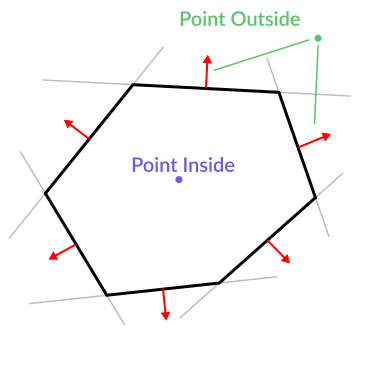
코드는 다음과 같아야 합니다:
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
꽤 멋지죠, 네? 하지만 이것은 훨씬 더 나아집니다! 조금만 더 노력하면, 유사한 논리가 우리에게 컨벡스(볼록) 폴리곤 두 개가 겹치는 때를 알려줄 것입니다. 이것을 분리축 이론(SAT)이라고 하며 대부분의 물리학 엔진은 이것을 콜리전을 감지하기 위해 사용합니다.
점을 사용하면 평면이 양의 거리를 반환하는지 확인하는 것으로 점이 외부에 있는지 여부를 충분히 알 수 있습니다. 다른 폴리곤을 사용하면 모두 기타 폴리곤 점 으로 양의 거리를 반환하는 평면을 찾아야 합니다. 이 확인은 A의 평면을 B의 점에 대해 수행한 다음 B의 평면을 A의 점에 대해 수행합니다:

코드는 다음과 같아야 합니다:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
보시다시피 평면은 매우 유용하며, 이것이 빙산의 일각일 뿐입니다. 여러분은 아마 볼록하지 않은 폴리곤에 무슨 일이 일어날지 궁금해 할 것입니다. 일반적으로 오목한 폴리곤은 작은 컨벡스(볼록) 폴리곤으로 분할하거나 BSP(요즘 많이 사용되지 않는 기술)와 같은 기술을 사용하여 처리됩니다.
3D에서 콜리전 감지¶
이것은 또 다른 보너스 비트인데, 이것은 인내심을 갖고 이 긴 튜토리얼을 따라가는 것에 대한 보상입니다. 여기 또 다른 지혜가 있습니다. 직접 사용 사례(Godot는 이미 콜리전 감지를 매우 잘 수행함)는 아니지만 거의 모든 물리적 엔진과 콜리전 감지 라이브러리에 사용됩니다 :)
컨벡스 모양을 2D로 변환하는 것이 콜리전 탐지에 유용했다는 것을 기억하시나요? 당신은 점이 컨벡스 모양 안에 있는지 또는 두 개의 2D 컨벡스 모양이 겹치는지를 탐지할 수 있습니다.
네, 3D에서도 작동합니다. 만일 두 개의 3D 다면체 모양이 충돌하면 분리면을 찾을 수 없습니다. 분리면이 발견되면 모양은 확실히 충돌하지 않습니다.
비트를 새로 고치려면 폴리곤 A의 모든 정점이 평면의 한 쪽에 있고 폴리곤 B의 모든 정점이 다른 쪽에 있음을 의미합니다. 이 평면은 항상 폴리곤 A 또는 폴리곤 B의 면 평면 중 하나입니다.
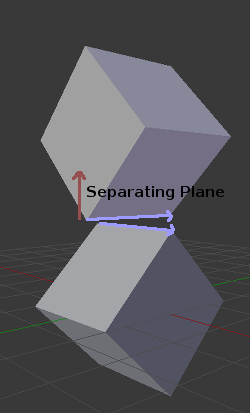
그러나 3D에서는 분리면을 찾을 수 없기 때문에 이 접근법에 문제가 있습니다. 다음은 이러한 상황의 예입니다:

이를 방지하려면 일부 추가 평면을 분리기로 테스트해야 합니다. 이러한 평면은 폴리곤 A의 모서리와 폴리곤 B의 모서리 사이의 외적입니다
마지막 알고리즘은 다음과 같습니다:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
더 많은 정보¶
Godot에서 벡터 수학을 사용하는 것에 대한 자세한 정보에 대해서는, 다음 글들을 참조하세요:
If you would like additional explanation, you should check out 3Blue1Brown's excellent video series "Essence of Linear Algebra": https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab