Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Dessin personnalisé en 2D¶
Introduction¶
Godot has nodes to draw sprites, polygons, particles, and all sorts of stuff. For most cases, this is enough. If there's no node to draw something specific you need, you can make any 2D node (for example, Control or Node2D based) draw custom commands.
Le dessin personnalisé dans un nœud 2D est vraiment utile. Voici quelques cas d'utilisation :
Dessiner des formes ou une logique que les nœuds existants ne peuvent pas faire, comme une image avec des traînées ou un polygone animé spécial.
Des visualisations qui ne sont pas très compatibles avec les nœuds, comme un plateau de tetris. (L'exemple du tetris utilise une fonction de dessin personnalisée pour dessiner les blocs.)
Dessiner un grand nombre d'objets simples. Le dessin personnalisé permet d'éviter la surcharge liée à l'utilisation d'un grand nombre de nœuds, ce qui peut réduire l'utilisation de la mémoire et améliorer les performances.
Création d'un contrôle d'interface utilisateur personnalisé. Il existe de nombreux contrôles disponibles, mais si vous avez des besoins inhabituels, vous aurez probablement besoin d'un contrôle personnalisé.
Dessin¶
Ajoutez un script à n'importe quel nœud dérivé de CanvasItem, comme Control ou Node2D. Puis remplacez la fonction _draw().
extends Node2D
func _draw():
# Your draw commands here
pass
public override void _Draw()
{
// Your draw commands here
}
Les commandes de dessin sont décrites dans la référence de classe CanvasItem. Elles sont nombreuses.
Mise à jour¶
La fonction _draw() n'est appelée qu'une fois, puis les commandes de dessin sont mises en mémoire tampon et mémorisées, de sorte que les appels ultérieurs sont inutiles.
If re-drawing is required because a state or something else changed,
call CanvasItem.queue_redraw()
in that same node and a new _draw() call will happen.
Voici un exemple un peu plus complexe. Une variable de texture qui sera redessinée si modifiée :
extends Node2D
@export var texture: Texture:
set = _set_texture
func _set_texture(value):
# If the texture variable is modified externally,
# this callback is called.
texture = value # Texture was changed.
queue_redraw() # Trigger a redraw of the node.
func _draw():
draw_texture(texture, Vector2())
using Godot;
public partial class MyNode2D : Node2D
{
private Texture _texture;
public Texture Texture
{
get
{
return _texture;
}
set
{
_texture = value;
QueueRedraw();
}
}
public override void _Draw()
{
DrawTexture(_texture, new Vector2());
}
}
In some cases, it may be desired to draw every frame. For this,
call queue_redraw() from the _process() callback, like this:
extends Node2D
func _draw():
# Your draw commands here
pass
func _process(delta):
queue_redraw()
using Godot;
public partial class CustomNode2D : Node2D
{
public override void _Draw()
{
// Your draw commands here
}
public override void _Process(double delta)
{
QueueRedraw();
}
}
Coordonnées¶
The drawing API uses the CanvasItem's coordinate system, not necessarily pixel coordinates. Which means it uses the coordinate space created after applying the CanvasItem's transform. Additionally, you can apply a custom transform on top of it by using draw_set_transform or draw_set_transform_matrix.
When using draw_line, you should consider the width of the line.
When using a width that is an odd size, the position should be shifted
by 0.5 to keep the line centered as shown below.
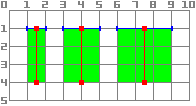
func _draw():
draw_line(Vector2(1.5, 1.0), Vector2(1.5, 4.0), Color.GREEN, 1.0)
draw_line(Vector2(4.0, 1.0), Vector2(4.0, 4.0), Color.GREEN, 2.0)
draw_line(Vector2(7.5, 1.0), Vector2(7.5, 4.0), Color.GREEN, 3.0)
public override void _Draw()
{
DrawLine(new Vector2(1.5f, 1.0f), new Vector2(1.5f, 4.0f), Colors.Green, 1.0f);
DrawLine(new Vector2(4.0f, 1.0f), new Vector2(4.0f, 4.0f), Colors.Green, 2.0f);
DrawLine(new Vector2(7.5f, 1.0f), new Vector2(7.5f, 4.0f), Colors.Green, 3.0f);
}
The same applies to the draw_rect method with filled = false.
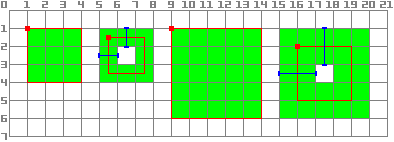
func _draw():
draw_rect(Rect2(1.0, 1.0, 3.0, 3.0), Color.GREEN)
draw_rect(Rect2(5.5, 1.5, 2.0, 2.0), Color.GREEN, false, 1.0)
draw_rect(Rect2(9.0, 1.0, 5.0, 5.0), Color.GREEN)
draw_rect(Rect2(16.0, 2.0, 3.0, 3.0), Color.GREEN, false, 2.0)
public override void _Draw()
{
DrawRect(new Rect2(1.0f, 1.0f, 3.0f, 3.0f), Colors.Green);
DrawRect(new Rect2(5.5f, 1.5f, 2.0f, 2.0f), Colors.Green, false, 1.0f);
DrawRect(new Rect2(9.0f, 1.0f, 5.0f, 5.0f), Colors.Green);
DrawRect(new Rect2(16.0f, 2.0f, 3.0f, 3.0f), Colors.Green, false, 2.0f);
}
Un exemple : dessiner des arcs de cercle¶
Nous allons maintenant utiliser la fonctionnalité de dessin personnalisé du moteur Godot pour dessiner quelque chose pour lequel Godot ne fournit pas de fonctions. À titre d'exemple, Godot fournit une fonction draw_circle() qui dessine un cercle entier. Cependant, qu'en est-il de dessiner une partie d'un cercle ? Vous devrez coder vous-même une fonction pour résoudre ça et la dessiner.
Fonction d'arc¶
Un arc est défini par les paramètres de son cercle. C'est-à-dire : la position centrale et le rayon. L'arc lui-même est alors défini par l'angle de départ et l'angle d'arrêt. Ce sont les 4 paramètres que nous devons fournir à notre dessin. Nous fournirons également la valeur de couleur afin que nous puissions dessiner l'arc de différentes couleurs si nous le souhaitons.
Fondamentalement, dessiner une forme à l'écran nécessite de la décomposer en un certain nombre de points liés de l'un à l'autre. Comme vous pouvez l’imaginer, plus votre forme est composée de points, plus elle paraîtra lisse, mais plus elle sera lourde en termes de coût de traitement. En général, si votre forme est énorme (ou en 3D, proche de la caméra), il faudra dessiner plus de points pour qu'elle n'ait pas un aspect anguleux. Au contraire, si votre forme est petite (ou en 3D, loin de la caméra), vous pouvez réduire son nombre de points pour diminuer le coût de traitement. Cela s'appelle Niveau de détail (LoD - Level of Details). Dans notre exemple, nous utiliserons simplement un nombre fixe de points, quel que soit le rayon.
func draw_circle_arc(center, radius, angle_from, angle_to, color):
var nb_points = 32
var points_arc = PackedVector2Array()
for i in range(nb_points + 1):
var angle_point = deg_to_rad(angle_from + i * (angle_to-angle_from) / nb_points - 90)
points_arc.push_back(center + Vector2(cos(angle_point), sin(angle_point)) * radius)
for index_point in range(nb_points):
draw_line(points_arc[index_point], points_arc[index_point + 1], color)
public void DrawCircleArc(Vector2 center, float radius, float angleFrom, float angleTo, Color color)
{
int nbPoints = 32;
var pointsArc = new Vector2[nbPoints + 1];
for (int i = 0; i <= nbPoints; i++)
{
float anglePoint = Mathf.DegToRad(angleFrom + i * (angleTo - angleFrom) / nbPoints - 90f);
pointsArc[i] = center + new Vector2(Mathf.Cos(anglePoint), Mathf.Sin(anglePoint)) * radius;
}
for (int i = 0; i < nbPoints - 1; i++)
{
DrawLine(pointsArc[i], pointsArc[i + 1], color);
}
}
Remember the number of points our shape has to be decomposed into? We fixed this
number in the nb_points variable to a value of 32. Then, we initialize an empty
PackedVector2Array, which is simply an array of Vector2s.
L'étape suivante consiste à calculer les positions réelles de ces 32 points qui composent un arc. Ceci est fait dans la première boucle for : nous itérons sur le nombre de points pour lesquels nous voulons calculer les positions, plus un pour inclure le dernier point. Nous déterminons d'abord l'angle de chaque point, entre les angles de départ et d'arrivée.
The reason why each angle is decreased by 90° is that we will compute 2D positions
out of each angle using trigonometry (you know, cosine and sine stuff...). However,
cos() and sin() use radians, not degrees. The angle of 0° (0 radian)
starts at 3 o'clock, although we want to start counting at 12 o'clock. So we decrease
each angle by 90° in order to start counting from 12 o'clock.
The actual position of a point located on a circle at angle angle (in radians)
is given by Vector2(cos(angle), sin(angle)). Since cos() and sin() return values
between -1 and 1, the position is located on a circle of radius 1. To have this
position on our support circle, which has a radius of radius, we simply need to
multiply the position by radius. Finally, we need to position our support circle
at the center position, which is performed by adding it to our Vector2 value.
Finally, we insert the point in the PackedVector2Array which was previously defined.
Maintenant, nous devons dessiner nos points. Comme vous pouvez l’imaginer, nous ne dessinerons pas simplement nos 32 points : nous devons dessiner tout ce qui les sépare. Nous aurions pu calculer nous-mêmes chaque point en utilisant la méthode précédente et les dessiner un à un. Mais ceci est trop compliqué et inefficace (sauf si explicitement requis). Donc, on trace simplement des lignes entre chaque paire de points. À moins que le rayon de notre cercle ne soit grand, la longueur de chaque ligne entre deux points ne sera jamais assez longue pour les voir. Si cela se produit, il nous faudra simplement augmenter le nombre de points.
Dessiner l'arc à l'écran¶
Nous avons maintenant une fonction qui dessine des choses à l'écran, il est temps de l'appeler dans la fonction _draw() :
func _draw():
var center = Vector2(200, 200)
var radius = 80
var angle_from = 75
var angle_to = 195
var color = Color(1.0, 0.0, 0.0)
draw_circle_arc(center, radius, angle_from, angle_to, color)
public override void _Draw()
{
var center = new Vector2(200, 200);
float radius = 80;
float angleFrom = 75;
float angleTo = 195;
var color = new Color(1, 0, 0);
DrawCircleArc(center, radius, angleFrom, angleTo, color);
}
Résultat :
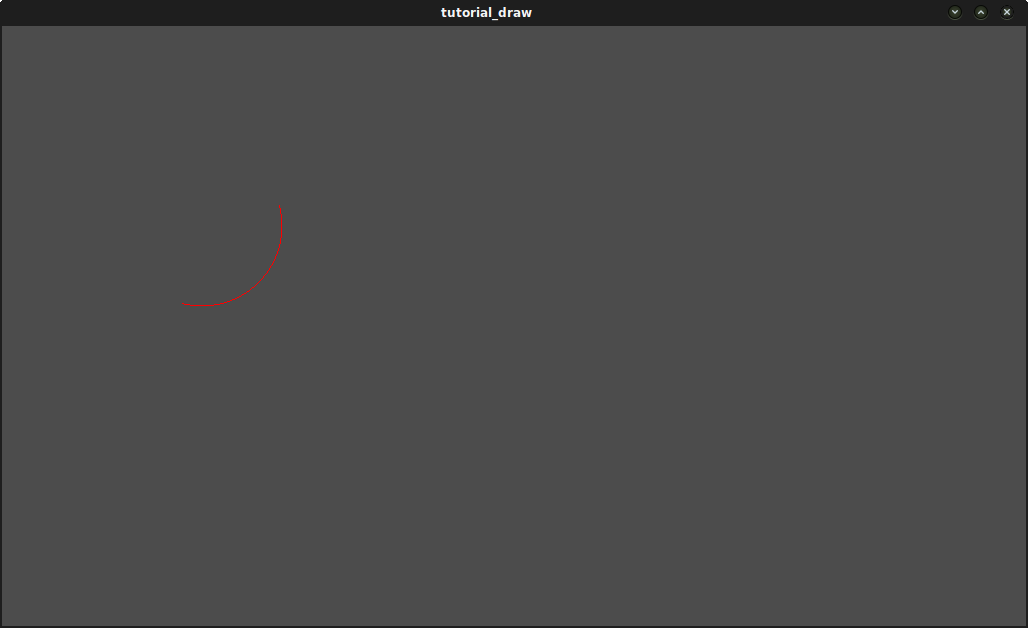
Fonction de polygone d'arc¶
Nous pouvons aller plus loin et écrire non seulement une fonction qui dessine la partie simple du disque définie par l’arc, mais aussi sa forme. La méthode est exactement la même que précédemment, sauf que nous dessinons un polygone au lieu de lignes :
func draw_circle_arc_poly(center, radius, angle_from, angle_to, color):
var nb_points = 32
var points_arc = PackedVector2Array()
points_arc.push_back(center)
var colors = PackedColorArray([color])
for i in range(nb_points + 1):
var angle_point = deg_to_rad(angle_from + i * (angle_to - angle_from) / nb_points - 90)
points_arc.push_back(center + Vector2(cos(angle_point), sin(angle_point)) * radius)
draw_polygon(points_arc, colors)
public void DrawCircleArcPoly(Vector2 center, float radius, float angleFrom, float angleTo, Color color)
{
int nbPoints = 32;
var pointsArc = new Vector2[nbPoints + 2];
pointsArc[0] = center;
var colors = new Color[] { color };
for (int i = 0; i <= nbPoints; i++)
{
float anglePoint = Mathf.DegToRad(angleFrom + i * (angleTo - angleFrom) / nbPoints - 90);
pointsArc[i + 1] = center + new Vector2(Mathf.Cos(anglePoint), Mathf.Sin(anglePoint)) * radius;
}
DrawPolygon(pointsArc, colors);
}

Dessin personnalisé dynamique¶
Nous sommes maintenant en mesure de dessiner des éléments personnalisés à l'écran. Cependant, c'est statique, faisons en sorte que cette forme tourne autour du centre. La solution consiste simplement à modifier les valeurs angle_from et angle_to dans le temps. Pour notre exemple, nous les incrémenterons simplement de 50. Cette valeur d’incrément doit rester constante sinon la vitesse de rotation changera en conséquence.
Premièrement, nous devons rendre globales, les variables angle_from et angle_to variables au début de notre script. Notez également que vous pouvez les stocker dans d'autres nœuds et y accéder à l'aide de get_node().
extends Node2D
var rotation_angle = 50
var angle_from = 75
var angle_to = 195
using Godot;
public partial class MyNode2D : Node2D
{
private float _rotationAngle = 50;
private float _angleFrom = 75;
private float _angleTo = 195;
}
Nous faisons en sorte que ces valeurs changent dans la fonction _process(delta).
Nous incrémentons également nos valeurs angle_from et angle_to ici. Cependant, il ne faut pas oublier de wrap() les valeurs résultantes entre 0 et 360° ! Autrement dit, si l'angle est de 361°, il est en fait de 1°. Si vous n'enveloppez pas ces valeurs, le script fonctionnera correctement, mais les valeurs d'angle deviendront de plus en plus grandes avec le temps jusqu'à atteindre la valeur entière maximale que Godot peut gérer (2^31 - 1). Lorsque cela se produit, Godot peut planter ou produire un comportement inattendu.
Finally, we must not forget to call the queue_redraw() function, which automatically
calls _draw(). This way, you can control when you want to refresh the frame.
func _process(delta):
angle_from += rotation_angle
angle_to += rotation_angle
# We only wrap angles when both of them are bigger than 360.
if angle_from > 360 and angle_to > 360:
angle_from = wrapf(angle_from, 0, 360)
angle_to = wrapf(angle_to, 0, 360)
queue_redraw()
public override void _Process(double delta)
{
_angleFrom += _rotationAngle;
_angleTo += _rotationAngle;
// We only wrap angles when both of them are bigger than 360.
if (_angleFrom > 360 && _angleTo > 360)
{
_angleFrom = Mathf.Wrap(_angleFrom, 0, 360);
_angleTo = Mathf.Wrap(_angleTo, 0, 360);
}
QueueRedraw();
}
De plus, n'oubliez pas de modifier la fonction _draw() pour faire usage de ces variables :
func _draw():
var center = Vector2(200, 200)
var radius = 80
var color = Color(1.0, 0.0, 0.0)
draw_circle_arc( center, radius, angle_from, angle_to, color )
public override void _Draw()
{
var center = new Vector2(200, 200);
float radius = 80;
var color = new Color(1, 0, 0);
DrawCircleArc(center, radius, _angleFrom, _angleTo, color);
}
Allons-y ! Cela fonctionne, mais l'arc tourne incroyablement vite ! Qu'est-ce qui ne va pas ?
La raison est que votre GPU affiche les images aussi rapidement que possible. Nous devons "normaliser" le dessin par cette vitesse. Pour ce faire, nous devons utiliser le paramètre delta de la fonction _process(). delta contient le temps écoulé entre les deux dernières images rendues. Il est généralement petit (environ 0,0003 seconde, mais cela dépend de votre matériel). Ainsi, l'utilisation de delta pour contrôler votre dessin assure que votre programme s'exécutera à la même vitesse sur le matériel de tout le monde.
Dans notre cas, nous devons simplement multiplier notre variable rotation_angle par delta dans la fonction _process(). De cette façon, nos 2 angles seront augmentés d'une valeur beaucoup plus petite, qui dépend directement de la vitesse de rendu.
func _process(delta):
angle_from += rotation_angle * delta
angle_to += rotation_angle * delta
# We only wrap angles when both of them are bigger than 360.
if angle_from > 360 and angle_to > 360:
angle_from = wrapf(angle_from, 0, 360)
angle_to = wrapf(angle_to, 0, 360)
queue_redraw()
public override void _Process(double delta)
{
_angleFrom += _rotationAngle * (float)delta;
_angleTo += _rotationAngle * (float)delta;
// We only wrap angles when both of them are bigger than 360.
if (_angleFrom > 360 && _angleTo > 360)
{
_angleFrom = Wrap(_angleFrom, 0, 360);
_angleTo = Wrap(_angleTo, 0, 360);
}
QueueRedraw();
}
Allons-y encore ! Cette fois, la rotation s'opère correctement !
Dessin avec anticrénelage¶
Godot offers method parameters in draw_line
to enable antialiasing, but not all custom drawing methods offer this antialiased
parameter.
For custom drawing methods that don't provide an antialiased parameter,
you can enable 2D MSAA instead, which affects rendering in the entire viewport.
This provides high-quality antialiasing, but a higher performance cost and only
on specific elements. See 2D antialiasing for more information.
Outils¶
Dessiner vos propres nœuds peut également être désiré lors de leur exécution dans l'éditeur pour les utiliser comme aperçu ou visualisation de certaines fonctionnalités ou comportements. Voir Exécuter le code dans l'éditeur pour plus d'informations.