Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Utiliser les transformations 3D¶
Introduction¶
Si vous n'avez jamais fait de jeux 3D auparavant, travailler avec des rotations en trois dimensions peut être déroutant au début. Venant de la 2D, la façon naturelle de penser est du genre "Oh, c'est comme tourner en 2D, sauf que maintenant les rotations se produisent en X, Y et Z ".
Au premier abord, cela semble facile et pour les jeux simples, cette façon de penser peut même être suffisante. Malheureusement, c'est souvent incorrect.
Les angles en trois dimensions sont le plus souvent appelés "angles d'Euler".
Les angles d'Euler ont été introduits par le mathématicien Leonhard Euler au début des années 1700.

Cette façon de représenter les rotations 3D était révolutionnaire à l'époque, mais elle a plusieurs défauts lorsqu'elle est utilisée dans le développement de jeux (ce qui est à attendre d'un gars avec un chapeau amusant). L'idée de ce document est d'expliquer pourquoi, ainsi que de présenter les meilleures pratiques pour gérer les transformations lors de la programmation de jeux 3D.
Problèmes des angles d’Euler¶
Bien qu'il puisse sembler intuitif que chaque axe ait une rotation, la vérité est que ce n'est tout simplement pas pratique.
Ordre des axes¶
La raison principale est qu'il n'y a pas de façon unique de construire une orientation à partir des angles. Il n'existe pas de fonction mathématique standard qui prend tous les angles ensemble et produit une rotation 3D. La seule façon de produire une orientation à partir des angles est de faire tourner l'objet angle par angle, dans un ordre arbitraire.
Ceci pourrait être fait en tournant d'abord dans X, puis dans Y et ensuite dans Z. Alternativement, vous pouvez d'abord tourner en Y, puis en Z et enfin en X. Tout fonctionne, mais selon l'ordre, l'orientation finale de l'objet ne sera pas nécessairement la même. En effet, cela signifie qu'il y a plusieurs façons de construire une orientation à partir de 3 angles différents, selon l'ordre des rotations.
Voici une visualisation des axes de rotation (dans l'ordre X, Y, Z) dans un cardan (de Wikipedia). Comme vous pouvez le voir, l'orientation de chaque axe dépend de la rotation du précédent :
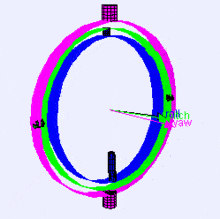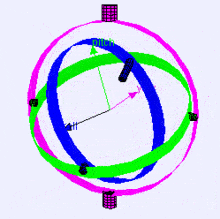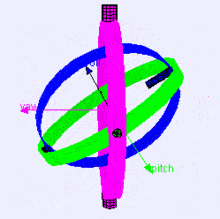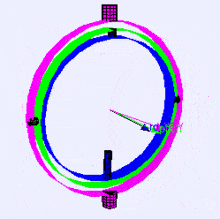
Vous vous demandez peut-être comment cela vous affecte. Prenons un exemple pratique :
Imaginez que vous travaillez sur un contrôleur à la première personne (par exemple, un jeu FPS). Déplacer la souris vers la gauche et vers la droite contrôle votre angle de vue parallèle au sol, tout en le déplaçant vers le haut et vers le bas déplace la vue du joueur vers le haut et vers le bas.
Dans ce cas, pour obtenir l'effet désiré, la rotation doit d'abord être appliquée sur l'axe Y (dans ce cas, Godot utilise une orientation "Y-Up"), puis sur l'axe X.

Si nous devions appliquer la rotation dans l'axe X d'abord, puis dans Y, l'effet serait undésirable :

Selon le type de jeu ou d'effet désiré, l'ordre dans lequel vous voulez que les rotations des axes soient appliquées peut varier. Par conséquent, il ne suffit pas d'appliquer des rotations en X, Y et Z : il vous faut également un ordre de rotation.
Interpolation¶
Un autre problème avec l'utilisation des angles d'Euler est l'interpolation. Imaginez que vous voulez faire la transition entre deux caméras différentes ou entre deux positions ennemies (y compris les rotations). Une façon logique d'y parvenir est d'interpoler les angles d'une position à l'autre. On pourrait s'attendre à ce que ça ressemble à ça :

Mais cela n'a pas toujours l'effet escompté lorsque l'on utilise les angles :

La caméra a en fait tourné dans la direction opposée !
Il y a plusieurs raisons à cela :
Les rotations ne correspondent pas linéairement à l'orientation, donc les interpoler n'aboutit pas toujours au chemin le plus court (passer de
270à0degrés n'est pas la même chose que passer de270à360, même si les angles sont équivalents).Le blocage de cardan est en jeu (le premier et le dernier axe de rotation s'alignent, ce qui entraîne une perte de liberté). Voir la page Wikipedia sur le blocage de cardan pour une explication détaillée de ce problème.
Dîtes non aux angles d’Euler¶
The result of all this is that you should not use the rotation property of Node3D nodes in Godot for games. It's there to be used mainly in the editor, for coherence with the 2D engine, and for simple rotations (generally just one axis, or even two in limited cases). As much as you may be tempted, don't use it.
Il existe une meilleure façon de résoudre vos problèmes de rotation.
Introduction aux transformations¶
Godot uses the Transform3D datatype for orientations. Each Node3D node contains a transform property which is relative to the parent's transform, if the parent is a Node3D-derived type.
Il est également possible d'accéder à la transformation des coordonnées du monde via la propriété global_transform.
Une transformation a un Basis (transform.basis sub-property), qui se compose de trois vecteurs Vector3. Ceux-ci sont accessibles via la propriété transform.basis et peuvent être accédés directement par transform.basis.x, transform.basis.y, et transform.basis.z. Chaque vecteur pointe dans la direction dans laquelle son axe a été tourné, de sorte qu'ils décrivent efficacement la rotation totale du nœud. L'échelle (tant qu'elle est uniforme) peut également être déduite de la longueur des axes. Une base peut aussi être interprétée comme une matrice 3x3 et utilisée comme transform.basis[x][y].
Une base par défaut (non modifiée) s'apparente à :
var basis = Basis()
# Contains the following default values:
basis.x = Vector3(1, 0, 0) # Vector pointing along the X axis
basis.y = Vector3(0, 1, 0) # Vector pointing along the Y axis
basis.z = Vector3(0, 0, 1) # Vector pointing along the Z axis
// Due to technical limitations on structs in C# the default
// constructor will contain zero values for all fields.
var defaultBasis = new Basis();
GD.Print(defaultBasis); // prints: ((0, 0, 0), (0, 0, 0), (0, 0, 0))
// Instead we can use the Identity property.
var identityBasis = Basis.Identity;
GD.Print(identityBasis.X); // prints: (1, 0, 0)
GD.Print(identityBasis.Y); // prints: (0, 1, 0)
GD.Print(identityBasis.Z); // prints: (0, 0, 1)
// The Identity basis is equivalent to:
var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);
GD.Print(basis); // prints: ((1, 0, 0), (0, 1, 0), (0, 0, 1))
C’est aussi un analogue d’une matrice d’identité 3 x 3.
Selon la convention OpenGL, X est l'axe Droite, Y est l'axe Haut et Z est l'axe Avant.
Ensemble avec la base, une transformation a aussi une origine. Il s'agit d'un Vector3 spécifiant à quelle distance de l'origine réelle (0, 0, 0, 0) cette transformation est. Combinant la base avec l'origine, une transformation représente efficacement une translation, une rotation et une mise à l'échelle dans l'espace.
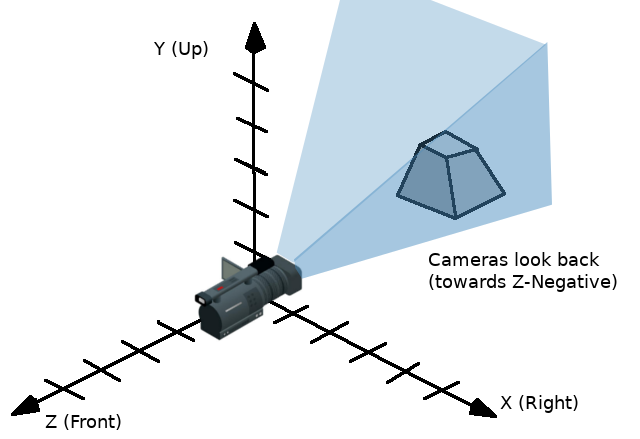
Une façon de visualiser une transformation est de regarder le gadget 3D d'un objet en mode "local space".

Les flèches du gadget indiquent les axes X, Y et Z (en rouge, vert et bleu respectivement) de la base, tandis que le centre du gadget est à l'origine de l'objet.

Pour plus d'informations sur les mathématiques des vecteurs et des transformations, veuillez lire les tutoriels Mathématiques des vecteurs.
Manipuler les transformations¶
Bien sûr, les transformations ne sont pas aussi simple à manipuler comme angles et ont leurs propres problèmes.
Il est possible de faire tourner une transformation, soit en multipliant sa base par une autre (c'est ce qu'on appelle l'accumulation), soit en utilisant les méthodes de rotation.
var axis = Vector3(1, 0, 0) # Or Vector3.RIGHT
var rotation_amount = 0.1
# Rotate the transform around the X axis by 0.1 radians.
transform.basis = Basis(axis, rotation_amount) * transform.basis
# shortened
transform.basis = transform.basis.rotated(axis, rotation_amount)
Transform3D transform = Transform;
Vector3 axis = new Vector3(1, 0, 0); // Or Vector3.Right
float rotationAmount = 0.1f;
// Rotate the transform around the X axis by 0.1 radians.
transform.Basis = new Basis(axis, rotationAmount) * transform.Basis;
// shortened
transform.Basis = transform.Basis.Rotated(axis, rotationAmount);
Transform = transform;
A method in Node3D simplifies this:
# Rotate the transform around the X axis by 0.1 radians.
rotate(Vector3(1, 0, 0), 0.1)
# shortened
rotate_x(0.1)
// Rotate the transform around the X axis by 0.1 radians.
Rotate(new Vector3(1, 0, 0), 0.1f);
// shortened
RotateX(0.1f);
Ceci permet de faire pivoter le nœud par rapport au nœud parent.
Pour faire pivoter par rapport à l'espace de l'objet (la propre transformation du nœud), utilisez ce qui suit :
# Rotate around the object's local X axis by 0.1 radians.
rotate_object_local(Vector3(1, 0, 0), 0.1)
// Rotate around the object's local X axis by 0.1 radians.
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);
Erreurs de précision¶
Effectuer des opérations successives sur les transformations entraînera une perte de précision due à une erreur à virgule flottante. Cela signifie que l'échelle de chaque axe peut ne plus être exactement "1,0" et qu'ils peuvent ne plus être exactement à "90" degrés les uns des autres.
Si une transformation est tournée à chaque image, elle finira par se déformer avec le temps. C'est inévitable.
Il y a deux façons différentes de gérer cela. La première est de orthonormaliser la transformation après un certain temps (peut-être une fois par image si vous la modifiez à chaque image) :
transform = transform.orthonormalized()
transform = transform.Orthonormalized();
Tous les axes auront à nouveau une longueur de 1,0 et seront à 90 degrés les uns des autres. Cependant, toute mise à l'échelle appliquée à la transformation sera perdue.
It is recommended you not scale nodes that are going to be manipulated; scale their children nodes instead (such as MeshInstance3D). If you absolutely must scale the node, then re-apply it at the end:
transform = transform.orthonormalized()
transform = transform.scaled(scale)
transform = transform.Orthonormalized();
transform = transform.Scaled(scale);
Obtenir l'information¶
Vous pensez peut-être qu'à ce stade : "D'accord, mais comment obtenir des angles à partir d'une transformation ?" Encore une fois, la réponse est : vous ne le faites pas. Vous devez faire de votre mieux pour arrêter de penser en angles.
Imaginez que vous avez besoin de tirer une balle dans la direction faisant face à votre joueur . Utilisez simplement l'axe avant (communément Z ou -Z).
bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED
bullet.Transform = transform;
bullet.LinearVelocity = transform.Basis.Z * BulletSpeed;
L'ennemi regarde-t-il le joueur ? Utilisez le produit scalaire pour cela (voir le tutoriel Mathématiques des vecteurs pour une explication du produit scalaire) :
# Get the direction vector from player to enemy
var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
enemy.im_watching_you(player)
// Get the direction vector from player to enemy
Vector3 direction = enemy.Transform.Origin - player.Transform.Origin;
if (direction.Dot(enemy.Transform.Basis.Z) > 0)
{
enemy.ImWatchingYou(player);
}
Déplacement latéral à gauche :
# Remember that +X is right
if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)
// Remember that +X is right
if (Input.IsActionPressed("strafe_left"))
{
TranslateObjectLocal(-Transform.Basis.X);
}
Sauter :
# Keep in mind Y is up-axis
if Input.is_action_just_pressed("jump"):
velocity.y = JUMP_SPEED
move_and_slide()
// Keep in mind Y is up-axis
if (Input.IsActionJustPressed("jump"))
velocity.Y = JumpSpeed;
MoveAndSlide();
Tous les comportements communs et logique peuvent être faits avec juste des vecteurs.
Informations de réglage¶
Il y a, bien sûr, des cas où vous voulez régler l'information sur une transformation. Imaginez une vue à la première personne ou une caméra orbitale. Celles-ci sont certainement faites en utilisant des angles, parce que vous voulez que les transformations se produisent dans un ordre spécifique.
For such cases, keep the angles and rotations outside the transform and set them every frame. Don't try to retrieve and reuse them because the transform is not meant to be used this way.
Exemple de regarder les alentours, en vue FPS :
# accumulators
var rot_x = 0
var rot_y = 0
func _input(event):
if event is InputEventMouseMotion and event.button_mask & 1:
# modify accumulated mouse rotation
rot_x += event.relative.x * LOOKAROUND_SPEED
rot_y += event.relative.y * LOOKAROUND_SPEED
transform.basis = Basis() # reset rotation
rotate_object_local(Vector3(0, 1, 0), rot_x) # first rotate in Y
rotate_object_local(Vector3(1, 0, 0), rot_y) # then rotate in X
// accumulators
private float _rotationX = 0f;
private float _rotationY = 0f;
public override void _Input(InputEvent @event)
{
if (@event is InputEventMouseMotion mouseMotion)
{
// modify accumulated mouse rotation
_rotationX += mouseMotion.Relative.X * LookAroundSpeed;
_rotationY += mouseMotion.Relative.Y * LookAroundSpeed;
// reset rotation
Transform3D transform = Transform;
transform.Basis = Basis.Identity;
Transform = transform;
RotateObjectLocal(Vector3.Up, _rotationX); // first rotate about Y
RotateObjectLocal(Vector3.Right, _rotationY); // then rotate about X
}
}
Comme vous pouvez le voir, dans de tels cas, il est encore plus simple de garder la rotation à l'extérieur, puis d'utiliser la transformation comme orientation finale.
Interpoler avec des quaternions¶
L'interpolation entre deux transformations peut se faire efficacement avec des quaternions. Plus d'informations sur le fonctionnement des quaternions peuvent être trouvées à d'autres endroits sur Internet. Pour l'usage pratique, il suffit de comprendre que leur utilisation principale est de faire une interpolation de la trajectoire la plus proche possible. Si vous avez deux rotations, un quaternion permettra l'interpolation entre elles en utilisant l'axe le plus proche.
Convertir une rotation en quaternion est très simple.
# Convert basis to quaternion, keep in mind scale is lost
var a = Quaternion(transform.basis)
var b = Quaternion(transform2.basis)
# Interpolate using spherical-linear interpolation (SLERP).
var c = a.slerp(b,0.5) # find halfway point between a and b
# Apply back
transform.basis = Basis(c)
// Convert basis to quaternion, keep in mind scale is lost
var a = transform.Basis.GetQuaternion();
var b = transform2.Basis.GetQuaternion();
// Interpolate using spherical-linear interpolation (SLERP).
var c = a.Slerp(b, 0.5f); // find halfway point between a and b
// Apply back
transform.Basis = new Basis(c);
The Quaternion type reference has more information on the datatype (it can also do transform accumulation, transform points, etc., though this is used less often). If you interpolate or apply operations to quaternions many times, keep in mind they need to be eventually normalized. Otherwise, they will also suffer from numerical precision errors.
Les quaternions sont utiles pour les interpolations caméra/chemin/etc. car le résultat sera toujours correct et lisse.
Les transformations sont vos amies¶
Pour la plupart des débutants, s'habituer à travailler avec des transformations peut prendre un certain temps. Cependant, une fois que vous vous y serez habitué, vous apprécierez leur simplicité et leur puissance.
N'hésitez pas à demander de l'aide à ce sujet dans n'importe laquelle des communautés en ligne de Godot et, une fois que vous aurez suffisamment confiance en vous, s'il vous plaît aider les autres !