Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Les matrices et les transformations¶
Introduction¶
Avant de lire ce tutoriel, nous vous recommandons de lire attentivement et de comprendre le tutoriel Mathématiques des vecteurs, car ce tutoriel nécessite une connaissance des vecteurs.
Ce tutoriel traite des transformations et de la façon dont nous les représentons dans Godot à l'aide de matrices. Il ne s'agit pas d'un guide complet et approfondi sur les matrices. Les transformations sont la plupart du temps appliquées sous forme de translation, de rotation et de mise à l'échelle. Nous nous concentrerons donc sur la façon de représenter celles-ci à l'aide de matrices.
La majeure partie de ce guide se concentre sur la 2D, en utilisant Transform2D et Vector2, mais la façon dont les choses fonctionnent en 3D est très similaire.
Note
Comme mentionné dans le précédent tutoriel, il est important de se rappeler que dans Godot, l'axe Y pointe vers le bas en 2D. C'est le contraire de la façon dont la plupart des écoles enseignent l'algèbre linéaire, avec l'axe Y pointant vers le haut.
Note
La convention est que l'axe X est rouge, l'axe Y est vert et l'axe Z est bleu. Ce tutoriel est codé par couleur pour correspondre à ces conventions, mais nous allons également représenter le vecteur d'origine avec une couleur bleue.
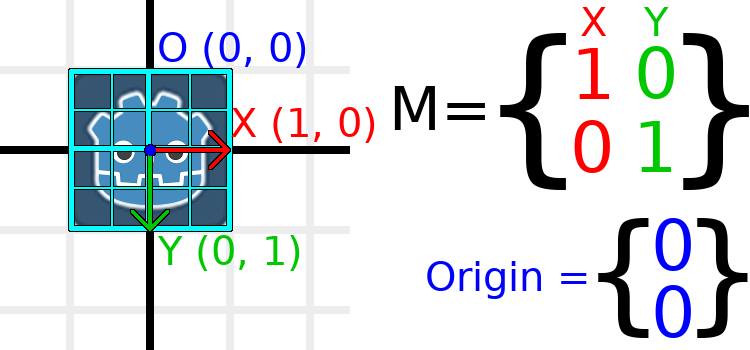
Composantes de la matrice et matrice d'identité¶
La matrice d'identité représente une transformation sans translation, sans rotation et sans mise à échelle. Commençons par regarder la matrice d'identité et comment ses composants sont liés à la façon dont elle apparaît visuellement.
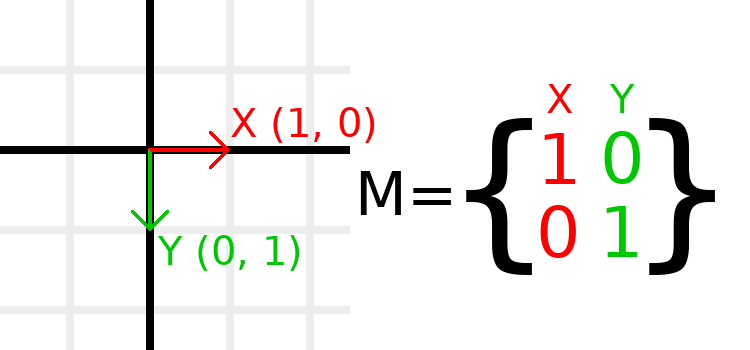
Les matrices ont des lignes et des colonnes, et une matrice de transformation a des conventions spécifiques sur ce que chacune fait.
Dans l'image ci-dessus, nous pouvons voir que le vecteur X rouge est représenté par la première colonne de la matrice, et le vecteur Y vert est également représenté par la deuxième colonne. Une modification des colonnes modifiera ces vecteurs. Nous verrons comment ils peuvent être manipulés dans les quelques exemples suivants.
Vous ne devez pas vous soucier de manipuler directement les lignes, car nous travaillons généralement avec les colonnes. Cependant, vous pouvez considérer les lignes de la matrice comme montrant quels vecteurs contribuent au déplacement dans une direction donnée.
When we refer to a value such as t.x.y, that's the Y component of
the X column vector. In other words, the bottom-left of the matrix.
Similarly, t.x.x is top-left, t.y.x is top-right, and t.y.y
is bottom-right, where t is the Transform2D.
Mise à l'échelle de la matrice de transformation¶
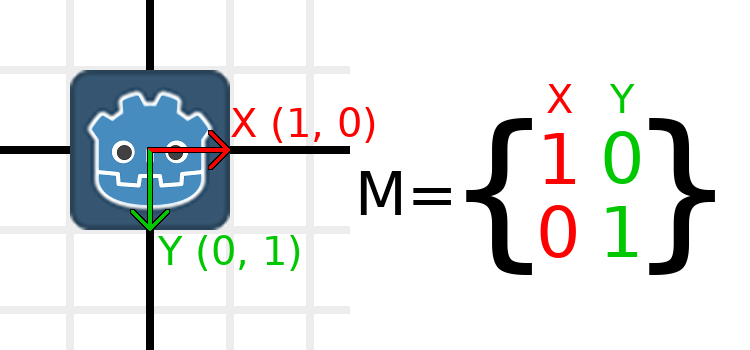
L'application d'une mise à l'échelle est l'une des opérations les plus faciles à comprendre. Commençons par placer le logo Godot sous nos vecteurs afin de pouvoir voir visuellement les effets sur un objet :
Maintenant, pour mettre la matrice à l'échelle, il suffit de multiplier chaque élément par l'échelle que nous voulons. Augmentons l'échelle de 2. 1 fois 2 devient 2, et 0 fois 2 devient 0, donc nous obtenons ceci :
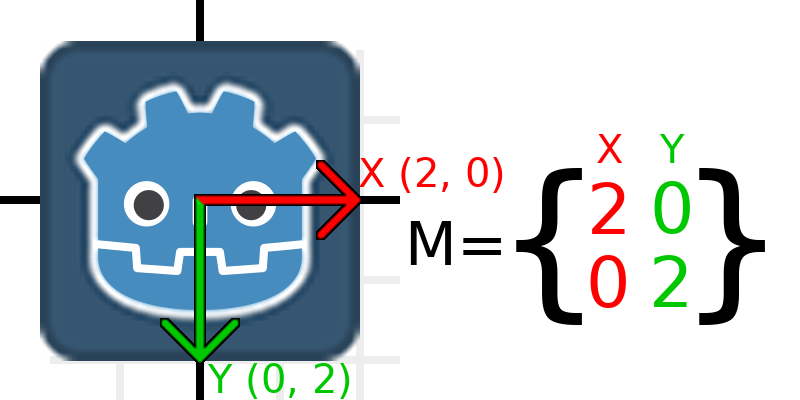
To do this in code, we multiply each of the vectors:
var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Scale
t.X *= 2;
t.Y *= 2;
Transform = t; // Change the node's transform to what we calculated.
Si nous voulions le ramener à son échelle initiale, nous pourrions multiplier chaque composante par 0,5. C'est à peu près tout ce qu'il y a à savoir pour mettre à l'échelle une matrice de transformation.
To calculate the object's scale from an existing transformation
matrix, you can use length() on each of the column vectors.
Note
In actual projects, you can use the scaled()
method to perform scaling.
Rotation de la matrice de transformation¶
Nous allons commencer de la même manière que précédemment, avec le logo Godot sous la matrice d'identité :

A titre d'exemple, disons que nous voulons faire pivoter notre logo Godot de 90 degrés dans le sens des aiguilles d'une montre. À l'heure actuelle, l'axe X pointe vers la droite et l'axe Y pointe vers le bas. Si nous les faisons pivoter dans notre tête, nous verrons logiquement que le nouvel axe X devrait pointer vers le bas et le nouvel axe Y vers la gauche.
Vous pouvez imaginer que vous saisissez à la fois le logo Godot et ses vecteurs, puis les tourner autour du centre. Où que vous finissiez la rotation, l'orientation des vecteurs détermine ce qu'est la matrice.
We need to represent "down" and "left" in normal coordinates,
so means we'll set X to (0, 1) and Y to (-1, 0). These are
also the values of Vector2.DOWN and Vector2.LEFT.
When we do this, we get the desired result of rotating the object:
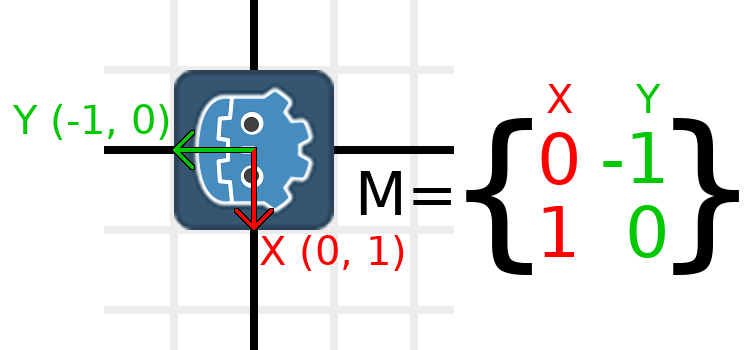
Si vous avez du mal à comprendre ce qui précède, essayez cet exercice : Coupez un carré de papier, tracez des vecteurs X et Y par-dessus, placez-le sur du papier millimétré, puis faites-le tourner et notez les points d'extrémité.
Pour effectuer une rotation en code, nous devons pouvoir calculer les valeurs via le programme. Cette image montre les formules nécessaires pour calculer la matrice de transformation à partir d'un angle de rotation. Ne vous inquiétez pas si cette partie vous semble compliquée, je vous promets que c'est la chose la plus difficile à savoir.
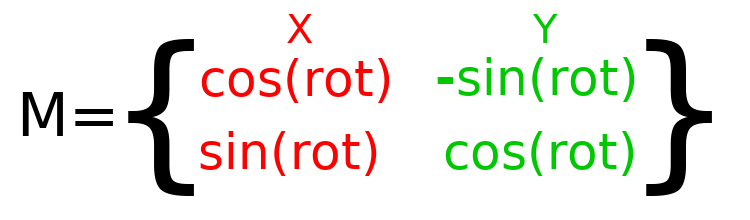
Note
Godot représente toutes les rotations avec des radians, pas des degrés. Un tour complet est en radians TAU ou PI*2, et un quart de tour de 90 degrés est en radians TAU/4 ou PI/2. Travailler avec TAU permet généralement d'obtenir un code plus lisible.
Note
Fait amusant : en plus du fait que Y soit en bas dans Godot, la rotation est représentée dans le sens des aiguilles d'une montre. Cela signifie que toutes les fonctions mathématiques et de trigonométrie se comportent de la même manière qu'un système CCW Y-is-up (Y est en haut), puisque ces différences "s'annulent". Vous pouvez penser que les rotations dans les deux systèmes sont "de X à Y".
In order to perform a rotation of 0.5 radians (about 28.65 degrees), we plug in a value of 0.5 to the formula above and evaluate to find what the actual values should be:
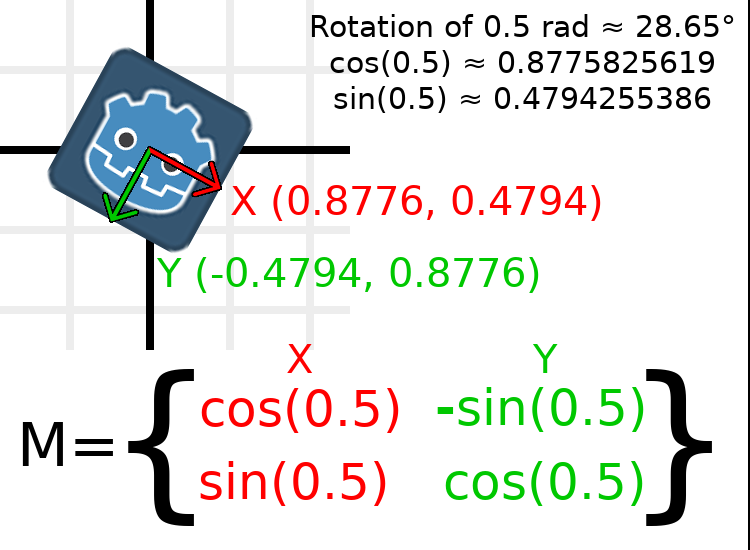
Voici comment cela serait fait en code (placer le script sur un Node2D) :
var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we calculated.
float rot = 0.5f; // The rotation to apply.
Transform2D t = Transform2D.Identity;
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
Transform = t; // Change the node's transform to what we calculated.
To calculate the object's rotation from an existing transformation
matrix, you can use atan2(t.x.y, t.x.x), where t is the Transform2D.
Note
In actual projects, you can use the rotated()
method to perform rotations.
Base de la matrice de transformation¶
So far we have only been working with the x and y, vectors, which
are in charge of representing rotation, scale, and/or shearing
(advanced, covered at the end). The X and Y vectors are together
called the basis of the transformation matrix. The terms "basis"
and "basis vectors" are important to know.
You might have noticed that Transform2D actually
has three Vector2 values: x, y, and origin.
The origin value is not part of the basis, but it is part of the
transform, and we need it to represent position. From now on we'll
keep track of the origin vector in all examples. You can think of
origin as another column, but it's often better to think of it as
completely separate.
Note that in 3D, Godot has a separate Basis structure for holding the three Vector3 values of the basis, since the code can get complex and it makes sense to separate it from Transform3D (which is composed of one Basis and one extra Vector3 for the origin).
Translation de la matrice de transformation¶
Changing the origin vector is called translating the transformation
matrix. Translating is basically a technical term for "moving" the
object, but it explicitly does not involve any rotation.
Travaillons à travers un exemple pour aider à comprendre cela. Nous commencerons par la transformation d'identité comme la dernière fois, sauf que nous allons suivre le vecteur d’origine cette fois.
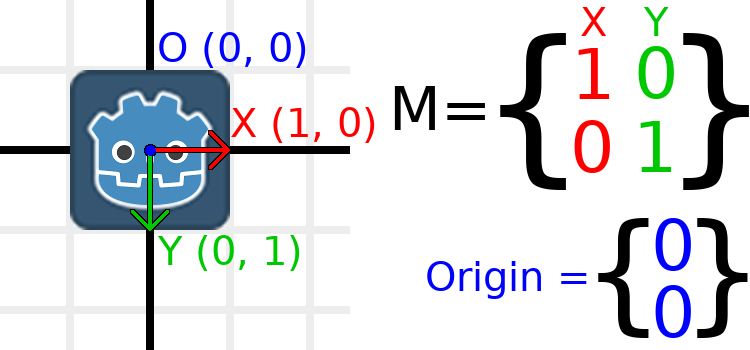
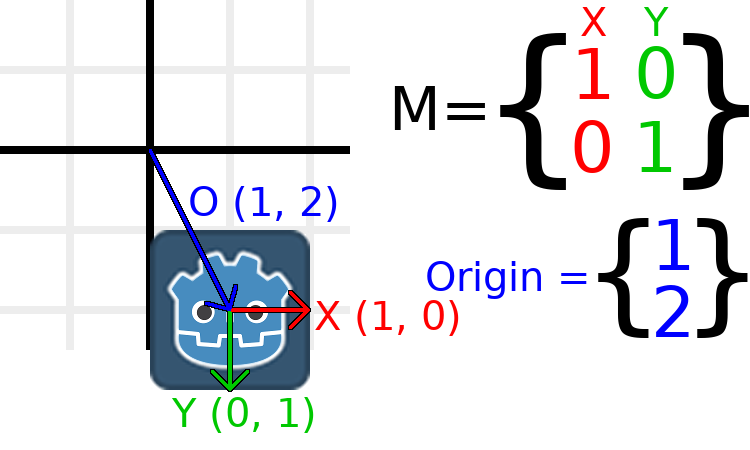
If we want to move the object to a position of (1, 2), we need
to set its origin vector to (1, 2):
There is also a translated() method, which performs a different
operation to adding or changing origin directly. The translated()
method will translate the object relative to its own rotation.
For example, an object rotated 90 degrees clockwise will move to
the right when translated() with Vector2.UP.
Note
La 2D de Godot utilise des coordonnées basées sur les pixels, donc dans les projets réels, vous voudrez translater par des centaines d'unités.
Mettre tout cela ensemble¶
We're going to apply everything we mentioned so far onto one transform. To follow along, create a project with a Sprite2D node and use the Godot logo for the texture resource.
Mettons la translation à (350, 150), une rotation de -0,5 rad, et une échelle de 3. J'ai posté une capture d'écran, et le code pour la reproduire, mais je vous encourage à essayer de reproduire la capture d'écran sans regarder le code !
var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Translation
t.Origin = new Vector2(350, 150);
// Rotation
float rot = -0.5f; // The rotation to apply.
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
// Scale
t.X *= 3;
t.Y *= 3;
Transform = t; // Change the node's transform to what we calculated.
Cisaillement de la matrice de transformation (avancé)¶
Note
Si vous cherchez seulement à savoir comment utiliser les matrices de transformation, n'hésitez pas à sauter cette section du tutoriel. Cette section explore un aspect peu utilisé des matrices de transformation dans le but d'en faciliter la compréhension.
Node2D provides a shearing property out of the box.
Vous avez peut-être remarqué qu'une transformation a plus de degrés de liberté que la combinaison des actions ci-dessus. La base d'une matrice de transformation 2D a quatre nombres totaux en deux valeurs Vector2, alors qu'une valeur de rotation et un Vector2 pour l'échelle n'ont que 3 nombres. Le concept de haut niveau pour le degré de liberté manquant est appelé cisaillement.
Normalement, les vecteurs de base seront toujours perpendiculaires entre eux. Cependant, le cisaillement peut être utile dans certaines situations, et comprendre le cisaillement vous aide à comprendre comment fonctionnent les transformations.
Pour vous montrer visuellement ce à quoi il ressemblera, superposons une grille au logo Godot :
Chaque point de cette grille est obtenu en additionnant les vecteurs de base. Le coin inférieur droit est X + Y, tandis que le coin supérieur droit est X - Y. Si nous changeons les vecteurs de base, toute la grille se déplace avec, car la grille est composée des vecteurs de base. Toutes les lignes de la grille qui sont actuellement parallèles le resteront, quelles que soient les modifications que nous apportons aux vecteurs de base.
À titre d'exemple, mettons Y à (1, 1) :
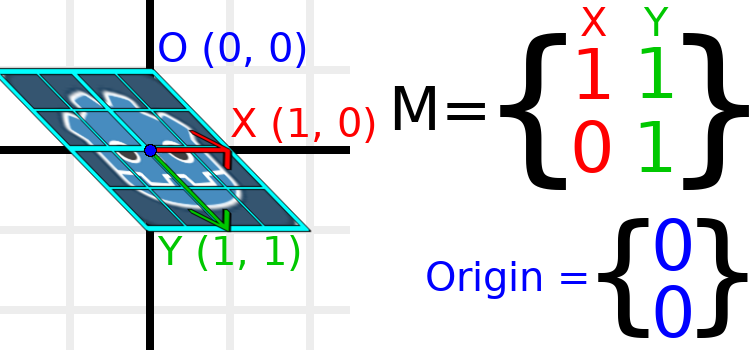
var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Shear by setting Y to (1, 1)
t.Y = Vector2.One;
Transform = t; // Change the node's transform to what we calculated.
Note
Vous ne pouvez pas définir les valeurs brutes d'un Transform2D dans l'éditeur, donc vous devez utiliser du code si vous voulez cisailler l'objet.
Les vecteurs n'étant plus perpendiculaires, l'objet a été cisaillé. Le centre inférieur de la grille, qui est (0, 1) par rapport à lui-même, est maintenant situé à une position mondiale de (1, 1).
Les coordonnées intra-objet sont appelées coordonnées UV dans les textures, alors empruntons cette terminologie pour ici. Pour trouver la position mondiale à partir d'une position relative, la formule est U * X + V * Y, où U et V sont des nombres et X et Y sont les vecteurs de base.
Le coin inférieur droit de la grille, qui est toujours à la position UV de (1, 1), est à la position mondiale de (2, 1), qui est calculée à partir de X*1 + Y*1, qui est (1, 0) + (1, 1), ou (1 + 1, 0 + 1), ou (2, 1). Cela correspond à notre observation de l'endroit où se trouve le coin inférieur droit de l'image.
De même, le coin supérieur droit de la grille, qui est toujours à la position UV de (1, -1), est à la position mondiale de (0, -1), qui est calculée à partir de X*1 + Y*-1, qui est (1, 0) - (1, 1), ou (1 - 1, 0 - 1), ou (0, -1). Cela correspond à notre observation de l'endroit où se trouve le coin supérieur droit de l'image.
Nous espérons que vous comprenez maintenant parfaitement comment une matrice de transformation affecte l'objet, et la relation entre les vecteurs de base et comment les "UV" ou "intra-coordonnées" de l'objet ont changé leur position dans le monde.
Note
Dans Godot, toutes les transformations mathématiques sont effectuées par rapport au nœud parent. Lorsque nous parlons de "position mondiale", ce serait plutôt par rapport au parent du nœud, si le nœud avait un parent.
Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur les transformations linéaires : https://www.youtube.com/watch?v=kYB8IZa5AuE
Applications pratiques des transformations¶
In actual projects, you will usually be working with transforms inside transforms by having multiple Node2D or Node3D nodes parented to each other.
However, it's useful to understand how to manually calculate the values we need. We will go over how you could use Transform2D or Transform3D to manually calculate transforms of nodes.
Convertir les positions entre les transformations¶
Il y a de nombreux cas où vous voudriez convertir une position dans et hors d'une transformation. Par exemple, si vous avez une position relative au joueur et que vous souhaitez trouver la position mondiale (par rapport au parent), ou si vous avez une position mondiale et que vous souhaitez savoir où elle se trouve par rapport au joueur.
We can find what a vector relative to the player would be defined in
world space as using the * operator:
# World space vector 100 units below the player.
print(transform * Vector2(0, 100))
// World space vector 100 units below the player.
GD.Print(Transform * new Vector2(0, 100));
And we can use the * operator in the opposite order to find a what world
space position would be if it was defined relative to the player:
# Where is (0, 100) relative to the player?
print(Vector2(0, 100) * transform)
// Where is (0, 100) relative to the player?
GD.Print(new Vector2(0, 100) * Transform);
Note
Si vous savez à l'avance que la transformation est positionnée à (0, 0), vous pouvez utiliser les méthodes "basis_xform" ou "basis_xform_inv" à la place, qui permettent d'éviter de traiter la translation.
Déplacement d'un objet par rapport à lui-même¶
Une opération courante, en particulier dans les jeux en 3D, consiste à déplacer un objet par rapport à lui-même. Par exemple, dans les jeux de tir à la première personne, vous voudriez que le personnage se déplace vers l'avant (axe -Z) lorsque vous appuyez sur W.
Since the basis vectors are the orientation relative to the parent, and the origin vector is the position relative to the parent, we can add multiples of the basis vectors to move an object relative to itself.
Ce code permet de déplacer un objet de 100 unités à sa propre droite :
transform.origin += transform.x * 100
Transform2D t = Transform;
t.Origin += t.X * 100;
Transform = t;
Pour se déplacer en 3D, il faudrait remplacer "x" par "basis.x".
Note
In actual projects, you can use translate_object_local in 3D
or move_local_x and move_local_y in 2D to do this.
Application de transformations sur des transformations¶
L'une des choses les plus importantes à savoir sur les transformations est la façon dont vous pouvez en utiliser plusieurs ensemble. La transformation d'un nœud parent affecte tous ses enfants. Disséquons un exemple.
Dans cette image, le nœud enfant a un "2" après les noms des composants pour les distinguer du nœud parent. Cela peut sembler un peu écrasant avec autant de chiffres, mais souvenez-vous que chaque chiffre est affiché deux fois (à côté des flèches et également dans les matrices), et que près de la moitié des chiffres sont des zéros.

Les seules transformations en cours ici sont que le nœud parent a reçu une échelle de (2, 1), l'enfant a reçu une échelle de (0,5, 0,5) et les deux nœuds ont reçu des positions.
All child transformations are affected by the parent transformations.
The child has a scale of (0.5, 0.5), so you would expect it to be
a 1:1 ratio square, and it is, but only relative to the parent.
The child's X vector ends up being (1, 0) in world space, because
it is scaled by the parent's basis vectors.
Similarly, the child node's origin vector is set to (1, 1), but this
actually moves it (2, 1) in world space, due to the parent node's
basis vectors.
Pour calculer manuellement la transformation de l'espace mondial d'un enfant, c'est le code que nous utiliserions :
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y
# Change the node's transform to what we calculated.
transform = Transform2D(basis_x, basis_y, origin)
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Calculate the child's world space transform
// origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
Vector2 origin = parent.X * child.Origin.X + parent.Y * child.Origin.Y + parent.Origin;
// basisX = (2, 0) * 0.5 + (0, 1) * 0 = (0.5, 0)
Vector2 basisX = parent.X * child.X.X + parent.Y * child.X.Y;
// basisY = (2, 0) * 0 + (0, 1) * 0.5 = (0.5, 0)
Vector2 basisY = parent.X * child.Y.X + parent.Y * child.Y.Y;
// Change the node's transform to what we calculated.
Transform = new Transform2D(basisX, basisY, origin);
In actual projects, we can find the world transform of the child by
applying one transform onto another using the * operator:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Change the node's transform to what would be the child's world transform.
transform = parent * child
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Change the node's transform to what would be the child's world transform.
Transform = parent * child;
Note
Quand on multiplie des matrices, l'ordre compte ! Ne les mélangez pas.
Enfin, appliquer la transformation d'identité ne fera rien.
Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur la composition des matrices : https://www.youtube.com/watch?v=XkY2DOUCWMU
Inverser une matrice de transformation¶
The "affine_inverse" function returns a transform that "undoes" the previous transform. This can be useful in some situations. Let's take a look at a few examples.
La multiplication d'une transformation inverse par la transformation normale annule toutes les transformations :
var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.
Transform2D ti = Transform.AffineInverse();
Transform2D t = ti * Transform;
// The transform is the identity transform.
Transforming a position by a transform and its inverse results in the same position:
var ti = transform.affine_inverse()
position = transform * position
position = ti * position
# The position is the same as before.
Transform2D ti = Transform.AffineInverse();
Position = Transform * Position;
Position = ti * Position;
// The position is the same as before.
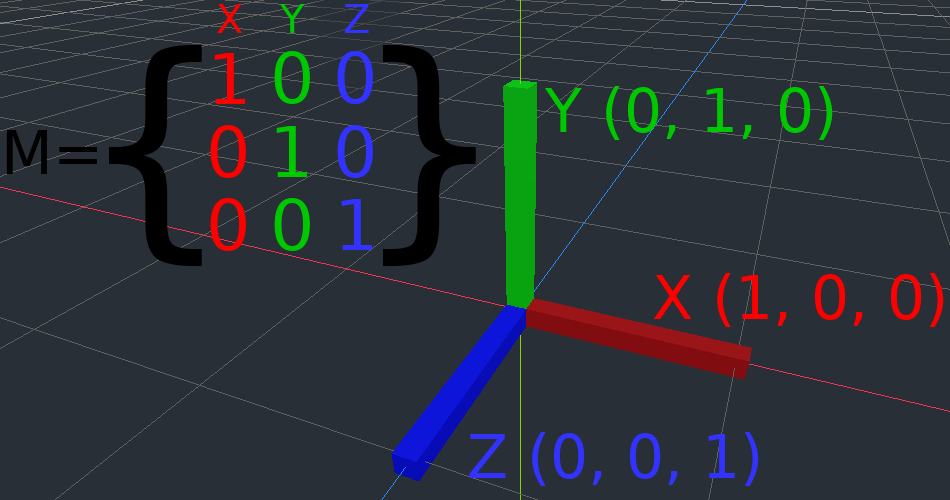
Comment tout cela fonctionne-t-il en 3D ?¶
One of the great things about transformation matrices is that they work very similarly between 2D and 3D transformations. All the code and formulas used above for 2D work the same in 3D, with 3 exceptions: the addition of a third axis, that each axis is of type Vector3, and also that Godot stores the Basis separately from the Transform3D, since the math can get complex and it makes sense to separate it.
Tous les concepts relatifs au fonctionnement de la translation, de la rotation, de l'échelle et du cisaillement en 3D sont les mêmes qu'en 2D. Pour l'échelle, nous prenons chaque composante et la multiplions ; pour la rotation, nous modifions l'endroit où chaque vecteur de base pointe ; pour la translation, nous manipulons l'origine ; et pour le cisaillement, nous modifions les vecteurs de base pour qu'ils soient non-perpendiculaires.
Si vous le souhaitez, il est bon de jouer avec les transformations pour comprendre leur fonctionnement. Godot vous permet d'éditer des matrices de transformation 3D directement depuis l'inspecteur. Vous pouvez télécharger ce projet qui comporte des lignes et des cubes colorés pour vous aider à visualiser les vecteurs Basis et l'origine en 2D et 3D : https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform
Note
You cannot edit Node2D's transform matrix directly in Godot 4.0's inspector. This may be changed in a future release of Godot.
Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente vidéo de 3Blue1Brown sur les transformations linéaires en 3D : https://www.youtube.com/watch?v=rHLEWRxRGiM
Représentation de la rotation en 3D (avancé)¶
La plus grande différence entre les matrices de transformation 2D et 3D est la façon dont vous représentez la rotation par elle-même sans les vecteurs de base.
With 2D, we have an easy way (atan2) to switch between a transformation matrix and an angle. In 3D, rotation is too complex to represent as one number. There is something called Euler angles, which can represent rotations as a set of 3 numbers, however, they are limited and not very useful, except for trivial cases.
In 3D we do not typically use angles, we either use a transformation basis (used pretty much everywhere in Godot), or we use quaternions. Godot can represent quaternions using the Quaternion struct. My suggestion to you is to completely ignore how they work under-the-hood, because they are very complicated and unintuitive.
Cependant, si vous voulez vraiment savoir comment cela fonctionne, voici quelques ressources intéressantes, que vous pouvez suivre dans l'ordre :
https://www.youtube.com/watch?v=mvmuCPvRoWQ