Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Mathématiques avancées des vecteurs¶
Plans¶
Le produit scalaire a une autre propriété intéressante avec les vecteurs unitaires. Imaginez que perpendiculairement à ce vecteur (et à travers l'origine) passe un plan. Les plans divisent tout l'espace en positif (au-dessus du plan) et négatif (sous le plan), et (contrairement à la croyance populaire) vous pouvez aussi utiliser leurs mathématiques en 2D :
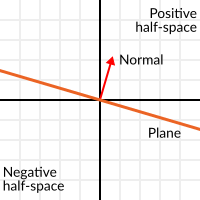
Les vecteurs unitaires sont perpendiculaires à une surface (ils décrivent donc l'orientation de la surface) sont appelés vecteurs unitaires normaux. Bien que, d'habitude, ils sont simplement abrégés comme normales. Les normales apparaissent dans les plans, la géométrie 3D (pour déterminer où chaque face ou sommet fait face), etc. Une normale est un vecteur unitaire, mais il est appelé normale à cause de son utilisation. (Tout comme nous appelons (0,0) l'origine !).
The plane passes by the origin and the surface of it is perpendicular to the unit vector (or normal). The side towards the vector points to is the positive half-space, while the other side is the negative half-space. In 3D this is exactly the same, except that the plane is an infinite surface (imagine an infinite, flat sheet of paper that you can orient and is pinned to the origin) instead of a line.
Distance par rapport au plan¶
Maintenant que ce qu'est un plan est clair, revenons au produit scalaire. Le produit scalaire entre un vecteur unitaire et n'importe quel point dans l'espace (oui, cette fois nous faisons le produit scalaire entre vecteur et position), renvoie la distance du point au plan :
var distance = normal.dot(point)
var distance = normal.Dot(point);
Mais pas seulement la distance absolue, si le point se trouve dans le demi-espace négatif, la distance sera également négative :
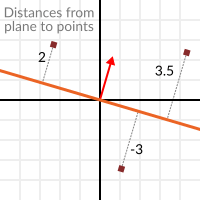
Cela nous permet de savoir de quel côté du plan est un point.
Loin de l'origine¶
Je sais ce que vous pensez ! Jusqu'à présent, c'est bien beau, mais les vrais plans sont partout dans l'espace, ne passant pas seulement par l'origine. Vous voulez de l'action plan réelle et vous la voulez maintenant.
Rappelez-vous que les plans non seulement divisent l'espace en deux, mais qu'ils ont aussi une polarité. Cela signifie qu'il est possible d'avoir des plans qui se chevauchent parfaitement, mais que leurs demi-espaces négatifs et positifs sont inversés.
Dans cette optique, décrivons un plan complet comme une normale N et une distance de l'origine scalaire D. Ainsi, notre plan est représenté par N et D. Par exemple :
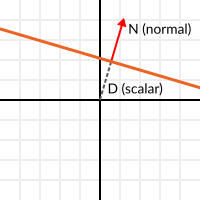
Pour les mathématiques 3D, Godot fournit un type intégré Plane qui gère cela.
Fondamentalement, N et D peuvent représenter n'importe quel plan dans l'espace, que ce soit pour de la 2D ou de la 3D (selon le nombre de dimensions de N) et les mathématiques sont les mêmes pour les deux. C'est le même chose qu'avant, mais D est la distance entre l'origine et le plan, se déplaçant dans la direction N. Par exemple, imaginez que vous voulez atteindre un point dans le plan, vous n'aurez qu'à faire :
var point_in_plane = N*D
var pointInPlane = N * D;
Ceci étirera (redimensionnera) le vecteur normale et le fera toucher le plan. Ce calcul peut sembler confus, mais c'est en fait beaucoup plus simple qu'il n'y paraît. Si nous voulons dire, encore une fois, la distance entre le point et le plan, nous faisons la même chose, mais en ajustant la distance :
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
La même chose, en utilisant une fonction intégrée :
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
Encore une fois, cela donnera une distance positive ou négative.
L'inversion de la polarité du plan peut se faire en rendant négatif N et D. Il en résultera un plan dans la même position, mais avec des demi-espaces négatifs et positifs inversés :
N = -N
D = -D
N = -N;
D = -D;
Godot also implements this operator in Plane. So, using the format below will work as expected:
var inverted_plane = -plane
var invertedPlane = -plane;
So, remember, the plane's main practical use is that we can calculate the distance to it. So, when is it useful to calculate the distance from a point to a plane? Let's see some examples.
Construire un plan en 2D¶
Il est clair que les plans ne sortent pas de nulle part, ils doivent donc être construits. Il est facile de les construire en 2D, soit à partir d'un vecteur normal (vecteur unitaire) et d'un point, soit à partir de deux points dans l'espace.
In the case of a normal and a point, most of the work is done, as the normal is already computed, so calculate D from the dot product of the normal and the point.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
Pour deux points dans l'espace, il y a en fait deux plans qui les traversent, partageant le même espace mais avec la normale pointant vers les directions opposées. Pour calculer la normale à partir des deux points, il faut d'abord obtenir le vecteur de direction, puis le faire pivoter de 90° de chaque côté :
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
The rest is the same as the previous example. Either point_a or point_b will work, as they are in the same plane:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Doing the same in 3D is a little more complex and is explained further down.
Quelques exemples de plan¶
Here is an example of what planes are useful for. Imagine you have a convex polygon. For example, a rectangle, a trapezoid, a triangle, or just any polygon where no faces bend inwards.
Pour chaque segment du polygone, nous calculons le plan qui passe par ce segment. Une fois que nous avons la liste des plans, nous pouvons faire des choses intéressantes, par exemple vérifier si un point est à l'intérieur du polygone.
Nous passons par tous les plans, si nous pouvons trouver un plan où la distance au point est positive, alors le point est à l'extérieur du polygone. Si on ne peut pas, alors le point est à l'intérieur.
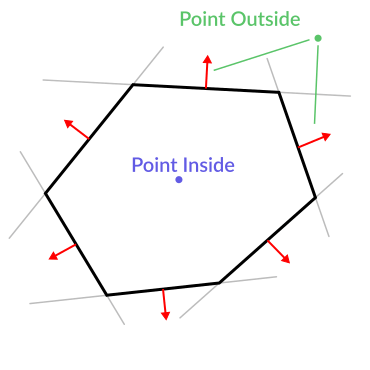
Le code devrait ressembler à ceci :
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
Plutôt cool, hein ? Mais encore mieux ! Avec un peu plus d'effort, une logique similaire nous permettra de savoir quand deux polygones convexes se chevauchent aussi. C'est ce qu'on appelle le théorème de l'axe de séparation (ou SAT) et la plupart des moteurs physiques l'utilisent pour détecter les collisions.
Avec un point, il suffit de vérifier si un plan retourne une distance positive pour savoir si le point est à l'extérieur. Avec un autre polygone, nous devons trouver un plan où tous les points de l'autre polygone lui renvoient une distance positive. Ce contrôle s'effectue avec les plans de A contre les points de B, puis avec les plans de B contre les points de A :
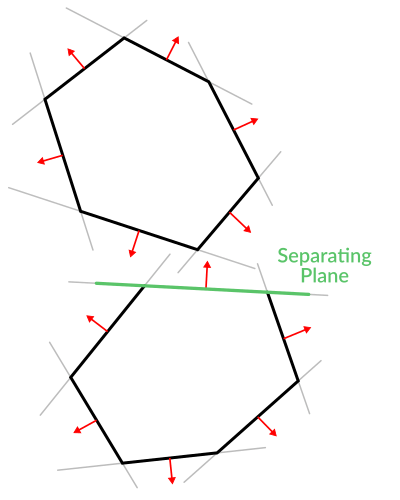
Le code devrait ressembler à ceci :
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Comme vous pouvez le constater, les plans sont très utiles, et ce n'est que la partie émergée de l'iceberg. Vous vous demandez peut-être ce qui se passe avec les polygones non convexes. Pour ce faire, il suffit généralement de diviser le polygone concave en polygones convexes plus petits ou d'utiliser une technique telle que le BSP (qui n'est pas très utilisé de nos jours).
Détection des collisions en 3D¶
C'est un autre bonus, une récompense pour avoir été patient et avoir suivi ce long tutoriel. Voici un autre morceau de sagesse. Ce n'est peut-être pas quelque chose avec un cas d'utilisation directe (Godot fait déjà assez bien la détection de collision) mais il est utilisé par presque tous les moteurs physiques et bibliothèques de détection de collision :)
Rappelez-vous que la conversion d'une forme convexe en 2D en un tableau de plans 2D a été utile pour la détection des collisions ? Vous pouviez détecter si un point se trouvait à l'intérieur d'une forme convexe, ou si deux formes convexes 2D se chevauchaient.
Eh bien, cela fonctionne aussi en 3D, si deux formes polyédriques 3D entrent en collision, vous ne pourrez pas trouver de plan de séparation. Si un plan de séparation est trouvé, les formes n'entrent définitivement pas en collision.
Rappelons-nous un peu, un plan de séparation signifie que tous les sommets du polygone A sont d'un côté du plan, et tous les sommets du polygone B sont de l'autre côté. Ce plan est toujours l'un des plans de face du polygone A ou du polygone B.
En 3D cependant, il y a un problème avec cette approche, car il est possible que, dans certains cas, un plan de séparation ne puisse être trouvé. Ceci est un exemple d'une telle situation :

Pour éviter cela, certains plans supplémentaires doivent être testés comme séparateurs, ces plans sont le produit vectoriel entre les bords du polygone A et les bords du polygone B
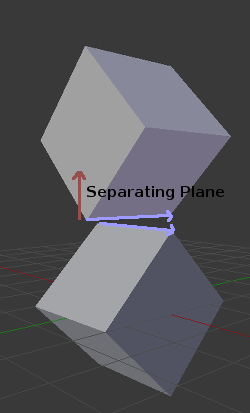
L'algorithme final est quelque chose comme cela :
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Plus d'information¶
Pour plus d'informations sur l'utilisation des mathématiques vectorielles dans Godot, voir les articles suivants :
Si vous souhaitez des explications supplémentaires, vous pouvez consulter l'excellente série vidéo de 3Blue1Brown "Essence of Linear Algebra" : https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab