Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Mathématiques des vecteurs¶
Introduction¶
Ce tutoriel est une introduction courte et pratique à l'algèbre linéaire telle qu'elle s'applique au développement de jeux. L'algèbre linéaire est l'étude des vecteurs et de leurs utilisations. Les vecteurs ont de nombreuses applications dans le développement 2D et 3D et Godot les utilise largement. Développer une bonne compréhension des mathématiques vectorielles est essentiel pour devenir un bon développeur de jeux.
Note
Ce tutoriel n'est pas un manuel formel sur l'algèbre linéaire. Nous n'examinerons que la façon dont elle est appliquée au développement de jeux. Pour un regard plus large sur les mathématiques, voir https://www.khanacademy.org/math/linear-algebra
Systèmes de coordonnées (2D)¶
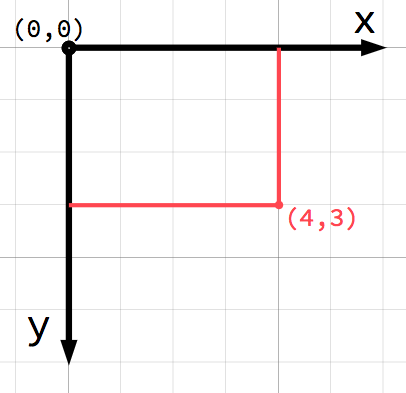
Dans l'espace 2D, les coordonnées sont définies par un axe horizontal (x) et un axe vertical (y). Une position particulière dans l'espace 2D s'écrit comme une paire de valeurs telles que (4, 3).
Note
Si vous êtes nouveau dans l'infographie, il peut sembler étrange que les points positifs de l'axe y soient orientés vers le bas plutôt que vers le haut, comme vous l'avez probablement appris en cours de mathématiques. Cependant, c'est commun dans la plupart des applications d'infographie.
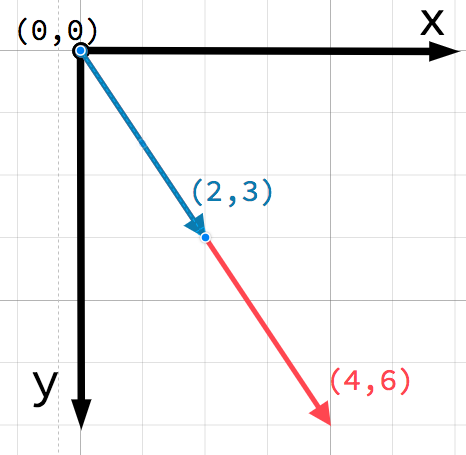
Toute position dans le plan 2D peut être identifiée par une paire de chiffres de cette façon. Cependant, on peut aussi considérer la position (4, 3) comme un décalage du point (0, 0), ou origine. Dessinez une flèche pointant de l'origine vers le point :
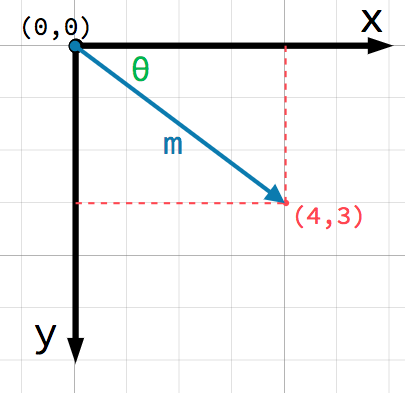
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
Un point très important à considérer au sujet des vecteurs est qu'ils ne représentent que la direction et l'amplitude relative. Il n'y a pas de notion de position d'un vecteur. Les deux vecteurs suivants sont identiques :
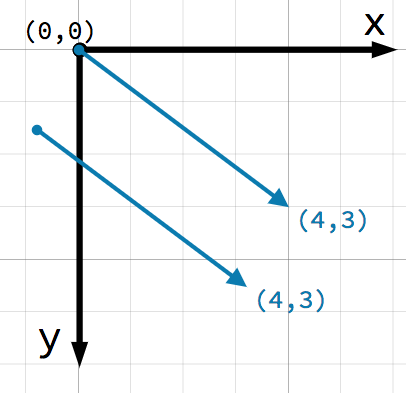
Les deux vecteurs représentent un point 4 unités à droite et 3 unités en dessous d'un point de départ. Peu importe où dans le plan vous dessinez le vecteur, il représente toujours une direction et une magnitude relatives.
Opérations vectorielles¶
Vous pouvez utiliser l'une ou l'autre méthode (coordonnées x et y ou angle et magnitude) pour faire référence à un vecteur, mais pour des raisons pratiques, les programmeurs utilisent généralement la notation des coordonnées. Par exemple, dans Godot, l'origine est le coin supérieur gauche de l'écran, donc pour placer un nœud 2D nommé Node2D 400 pixels à droite et 300 pixels en bas, utilisez le code suivant :
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
Accès aux membres¶
Les composants individuels du vecteur sont directement accessibles par leur nom.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Additionner des vecteurs¶
Lors de l'addition ou de la soustraction de deux vecteurs, les composants correspondants sont ajoutés :
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
Nous pouvons aussi le voir visuellement en ajoutant le deuxième vecteur à la fin du premier :
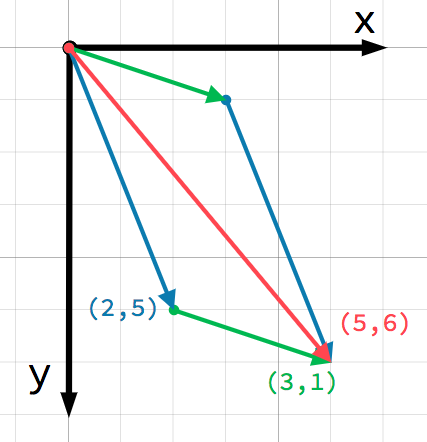
Notez que l'ajout de a + b donne le même résultat que b + a.
Multiplication scalaire¶
Note
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
Un vecteur peut être multiplié par un scalaire :
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Note
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
Applications pratiques¶
Examinons deux utilisations courantes de l'addition et de la soustraction de vecteurs.
Mouvement¶
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
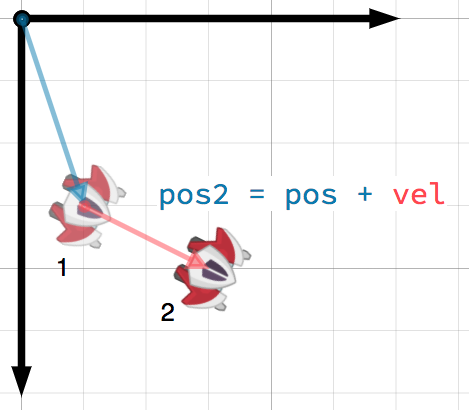
Astuce
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
Pointer vers une cible¶
Dans ce scénario, vous avez un tank qui souhaite diriger sa tourelle vers un robot. En soustrayant la position du tank de la position du robot, on obtient le vecteur pointant du tank vers le robot.
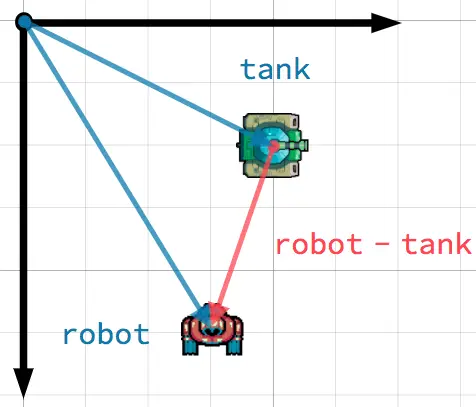
Astuce
To find a vector pointing from A to B, use B - A.
Vecteurs unitaires¶
Un vecteur avec une magnitude de 1 est appelé un vecteur unitaire. Ils sont aussi parfois appelés vecteurs de direction ou normales. Les vecteurs unitaires sont utiles lorsque vous avez besoin de suivre une direction.
Normalisation¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
Avertissement
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
Réflexion¶
Une utilisation courante des vecteurs unitaires est d'indiquer les normales. Les normales (ou vecteurs normaux) sont des vecteurs unitaires alignés perpendiculairement à une surface, définissant sa direction. Ils sont couramment utilisés pour l'éclairage, les collisions et d'autres opérations impliquant des surfaces.
Par exemple, imaginez que nous avons une balle en mouvement que nous voulons faire rebondir sur un mur ou un autre objet :
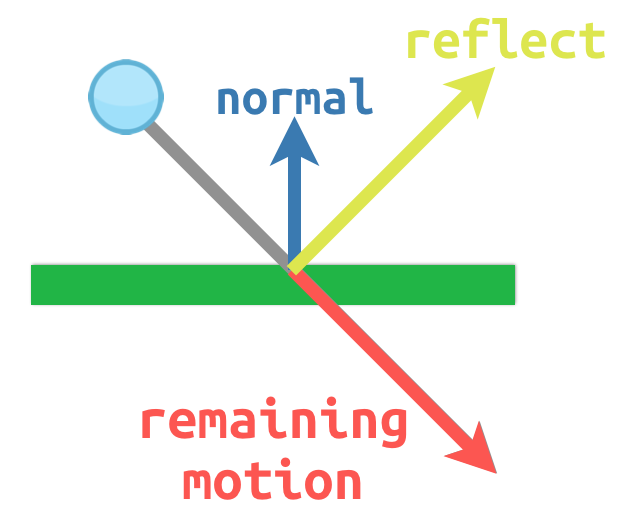
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Produit scalaire¶
Le produit scalaire est l'un des concepts les plus importants en mathématiques vectorielles, mais il est souvent mal compris. Le produit scalaire est une opération sur deux vecteurs qui retourne un scalaire. Contrairement à un vecteur, qui contient à la fois la magnitude et la direction, une valeur scalaire n'a que la magnitude.
La formule du produit scalaire prend deux formes courantes :
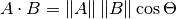
et
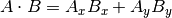
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
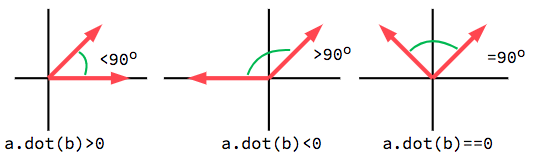
Lorsque vous utilisez des vecteurs unitaires, le résultat sera toujours compris entre -1 (180°) et 1 (0°).
Orienté vers¶
Nous pouvons utiliser ce fait pour détecter si un objet est orienté vers un autre objet. Dans le diagramme ci-dessous, le joueur P essaie d'éviter les zombies A et B. En supposant que le champ de vision d'un zombie est de 180°, peuvent-ils voir le joueur ?
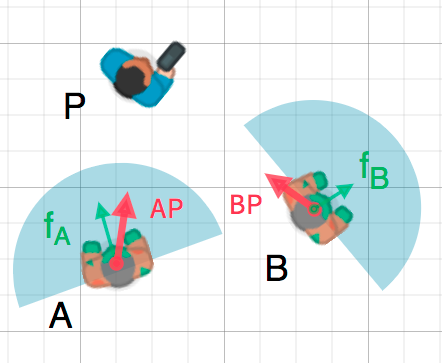
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
En code, cela ressemblerait à ceci :
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Produit Vectoriel¶
Comme le produit scalaire, le produit vectoriel est une opération sur deux vecteurs. Cependant, le résultat du produit vectoriel est un vecteur dont la direction est perpendiculaire aux deux. Sa magnitude dépend de leur angle relatif. Si deux vecteurs sont parallèles, le résultat de leur produit vectoriel sera un vecteur nul.

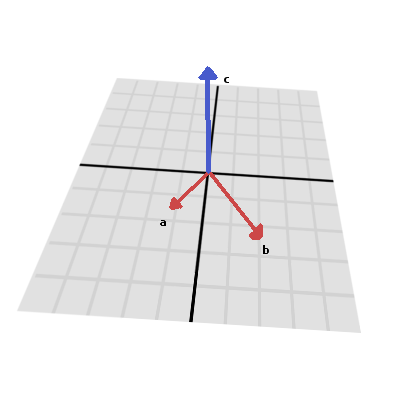
Le produit vectoriel est calculé de cette façon :
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
Note
Dans le produit vectoriel, l'ordre compte. a.cross(b) ne donne pas le même résultat que b.cross(a). Les vecteurs résultants pointent dans des directions contraires.
Calcul des normales¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
Voici une fonction pour calculer la normale d'un triangle :
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Pointer vers une cible¶
Dans la section sur le produit scalaire ci-dessus, nous avons vu comment il pouvait être utilisé pour trouver l'angle entre deux vecteurs. Cependant, en 3D, cette information n'est pas suffisante. Il faut aussi savoir autour de quel axe tourner. On peut le trouver en calculant le produit vectoriel de la direction actuelle et de la direction cible. Le vecteur perpendiculaire résultant est l'axe de rotation.
Plus d'information¶
Pour plus d'informations sur l'utilisation des mathématiques vectorielles dans Godot, voir les articles suivants :