Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Wektory¶
Wprowadzenie¶
Ten samouczek jest krótkim i praktycznym wprowadzeniem do algebry liniowej w zakresie tworzenia gier. Algebra liniowa jest badaniem wektorów i ich zastosowań. Wektory mają wiele zastosowań zarówno w 2D, jak i 3D, a Godot używa ich w szerokim zakresie. Dobre zrozumienie matematyki wektorowej jest niezbędne, aby stać się potężnym twórcą gier.
Informacja
Ten samouczek nie jest formalnym podręcznikiem na temat algebry liniowej. Będziemy się przyglądać tylko temu, w jaki sposób jest ona stosowany do tworzenia gier. Szersze spojrzenie ten poddział matematyki można znaleźć na stronie https://www.khanacademy.org/math/linear-algebra
Układy współrzędnych (2D)¶
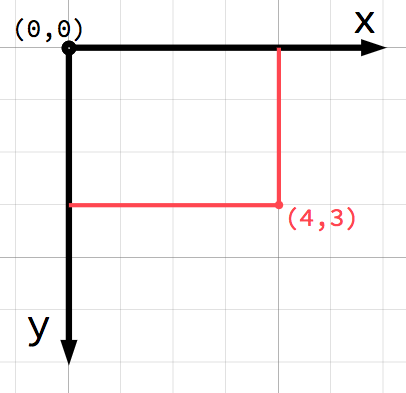
W przestrzeni 2D współrzędne są definiowane za pomocą osi poziomej ( x) i osi pionowej ( y). Położenie w przestrzeni 2D jest zapisywane jako para wartości takich jak (4, 3).
Informacja
Jeśli jesteś nowicjuszem w grafice komputerowej, może wydawać się dziwne, że dodatnie wartości osi y są skierowane w dół zamiast w górę, jak prawdopodobnie uczyliście się na lekcji matematyki. Jest to jednak powszechne w większości aplikacji graficznych.
W ten sposób można zidentyfikować dowolne położenie w płaszczyźnie 2D za pomocą pary liczb. Jednakże możemy również myśleć o pozycji (4, 3) jako przesunięcie od punktu (0, 0) lub źródło. Narysuj strzałkę wskazującą od początku do końca:
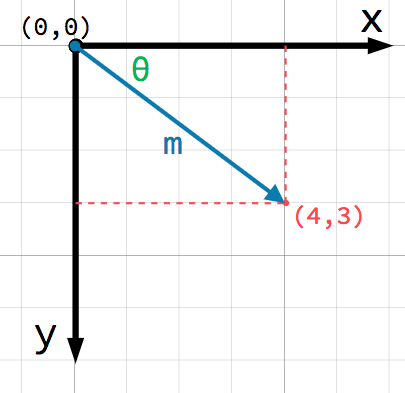
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
Bardzo ważną kwestią, którą należy wziąć pod uwagę w przypadku wektorów, jest to, że reprezentują one jedynie względny kierunek i wielkość. Nie istnieje pojęcie pozycji wektora. Następujące dwa wektory są identyczne:
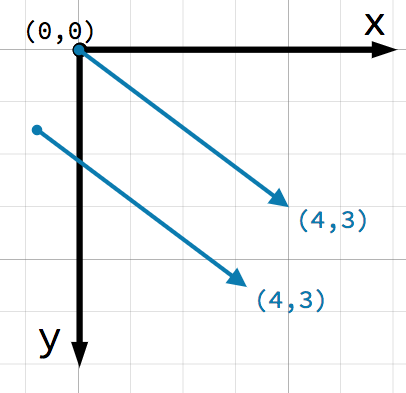
Oba wektory reprezentują punkt to samo, 4 jednostki w prawą stronę i 3 jednostki w dół od pewnego punktu początkowego. Nie ma znaczenia, gdzie na płaszczyźnie rysujesz wektor, zawsze reprezentuje on względny kierunek i wielkość.
Vector operations¶
You can use either method (x and y coordinates or angle and magnitude) to refer
to a vector, but for convenience, programmers typically use the coordinate
notation. For example, in Godot, the origin is the top-left corner of the
screen, so to place a 2D node named Node2D 400 pixels to the right and 300
pixels down, use the following code:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
Member access¶
Poszczególne komponenty wektora są dostępne bezpośrednio po nazwie.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Dodawanie wektorów¶
Podczas dodawania lub odejmowania dwóch wektorów dodawane są odpowiednie składniki:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
Widzimy to również wizualnie, dodając drugi wektor na końcu pierwszego:
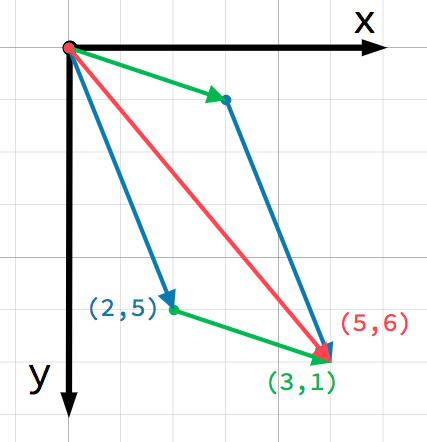
Należy pamiętać, że dodanie a + b daje taki sam rezultat jak b + a.
Mnożenie skalarne¶
Informacja
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
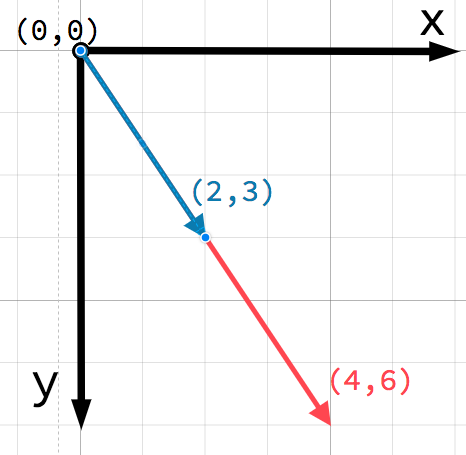
Wektor można pomnożyć przez skalar:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Informacja
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
Praktyczne zastosowania¶
Przyjrzyjmy się dwóm powszechnym zastosowaniom dodawania i odejmowania wektorów.
Ruch¶
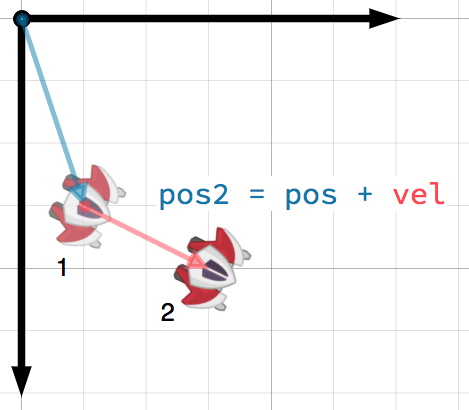
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
Wskazówka
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
Pointing toward a target¶
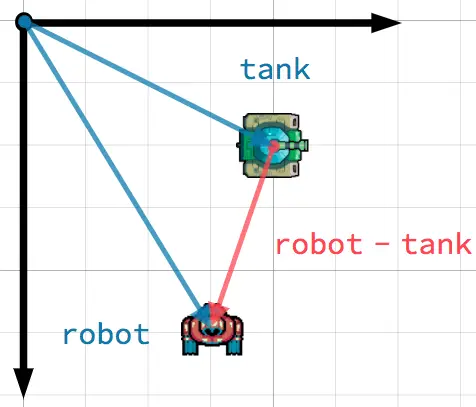
In this scenario, you have a tank that wishes to point its turret at a robot. Subtracting the tank's position from the robot's position gives the vector pointing from the tank to the robot.
Wskazówka
To find a vector pointing from A to B, use B - A.
Unit vectors¶
A vector with magnitude of 1 is called a unit vector. They are also
sometimes referred to as direction vectors or normals. Unit vectors are
helpful when you need to keep track of a direction.
Normalizacja¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
Ostrzeżenie
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
Odbicie¶
A common use of unit vectors is to indicate normals. Normal vectors are unit vectors aligned perpendicularly to a surface, defining its direction. They are commonly used for lighting, collisions, and other operations involving surfaces.
Wyobraźmy sobie na przykład, że mamy ruchomą kulę, którą chcemy odbić od ściany lub innego obiektu:
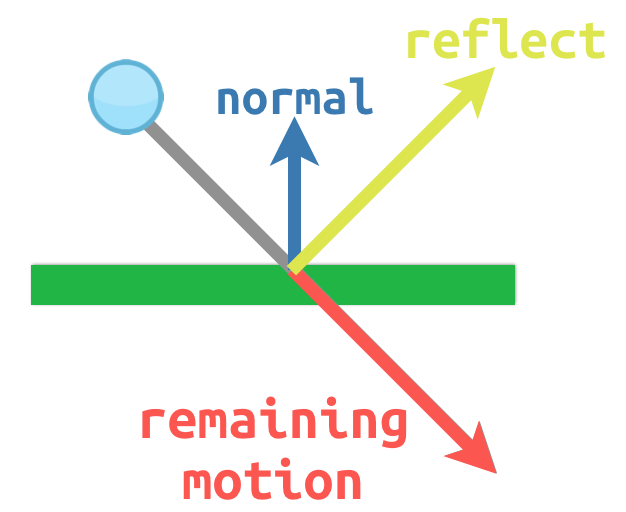
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Iloczyn skalarny¶
Wartość skalarna jest jednym z najważniejszych pojęć w matematyce wektorowej, ale często jest źle rozumiany. Wartość skalarna to operacja na dwóch wektorach, która zwraca skalar. W przeciwieństwie do wektora, który zawiera zarówno wielkość, jak i kierunek, wartość skalarna ma tylko wielkość.
The formula for dot product takes two common forms:
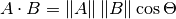
i
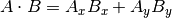
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
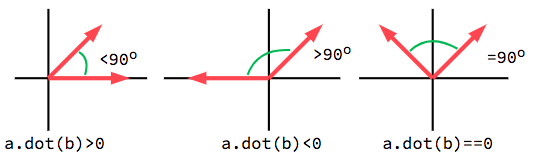
Przy zastosowaniu wektorów jednostkowych wynik zawsze będzie pomiędzy -1 (180°) a 1 (0°).
Facing¶
We can use this fact to detect whether an object is facing toward another
object. In the diagram below, the player P is trying to avoid the zombies
A and B. Assuming a zombie's field of view is 180°, can they see the
player?
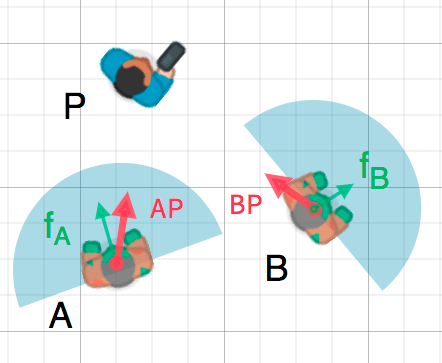
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
In code it would look like this:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Cross product¶
Like the dot product, the cross product is an operation on two vectors. However, the result of the cross product is a vector with a direction that is perpendicular to both. Its magnitude depends on their relative angle. If two vectors are parallel, the result of their cross product will be a null vector.

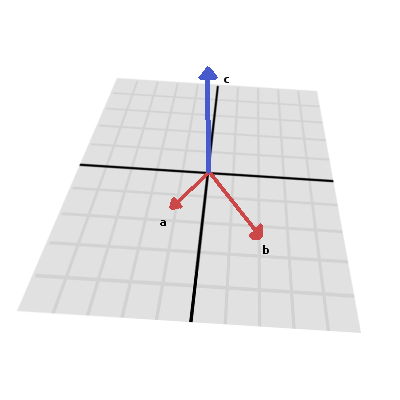
The cross product is calculated like this:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
Informacja
In the cross product, order matters. a.cross(b) does not give the
same result as b.cross(a). The resulting vectors point in
opposite directions.
Calculating normals¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
Here is a function to calculate a triangle's normal:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Pointing to a target¶
In the dot product section above, we saw how it could be used to find the angle between two vectors. However, in 3D, this is not enough information. We also need to know what axis to rotate around. We can find that by calculating the cross product of the current facing direction and the target direction. The resulting perpendicular vector is the axis of rotation.
More information¶
Więcej informacji na temat używania matematyki wektorowej w Godocie można znaleźć w poniższych artykułach: