Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
3D変換を使用する¶
はじめに¶
今まで3Dゲームを作成したことがない場合、3Dの回転操作は最初は混乱する可能性があります。 2Dから来る自然な考え方は、「ああ、2Dで回転するのと同じですね。X、Y、Zで回転が発生するようになったのですね」というものです。
最初は簡単そうに思えます。単純なゲームならこの考え方で十分かもしれません。しかし残念なことにそれはしばしば間違っています。
3次元の角度は、最も一般的には「オイラー角」と呼ばれます。
オイラー角は、1700年代初頭に数学者レオンハルトオイラーによって導入されました。

この3D回転の表現方法は当時画期的でしたが、ゲーム開発で使用するといくつかの欠点があります(これは面白い帽子をかぶった男から期待されることです)。このドキュメントの目的は、3Dゲームのプログラミング時に変換を処理するためのベストプラクティスを概説するだけでなく、その理由を説明することです。
オイラー角の問題点¶
各軸に回転があることは直感的に思えるかもしれませんが、実際には実際的ではありません。
軸の順序¶
これの主な理由は、角度から方向を構築する唯一無二の方法がないことです。すべての角度をまとめて実際の3D回転を生成する標準的な数学関数はありません。角度から方向を生成できる唯一の方法は、任意の順序で、各角度ごとにオブジェクトを回転させることです。
これは、最初に X で、次に Y で、次に Z で回転することで実行できます。または、最初に Y で回転し、次に Z で、最後に X で回転することもできます。何でも機能しますが、順序によっては、オブジェクトの最終的な向きは必ずしも同じではありません。実際、これは、回転の順序に応じて、3つの異なる角度から方向を構築するいくつかの方法があることを意味します。
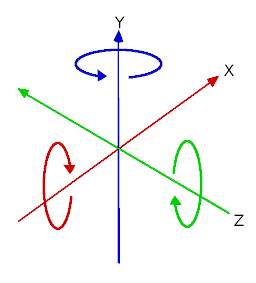
以下は、ジンバルでの回転軸(X、Y、Z順)の視覚化です(Wikipediaから)。ご覧のとおり、各軸の方向は前の軸の回転に依存します:
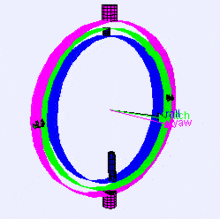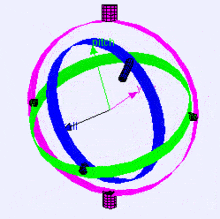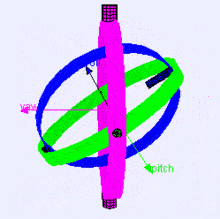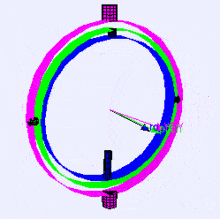
これがあなたにどのように影響するか疑問に思うかもしれません。実際の例を見てみましょう:
一人称コントローラー(FPSゲームなど)で作業していると想像してください。マウスを左右に動かすと、ビューアングルが地面と平行になり、上下に動かすと、プレイヤーのビューが上下します。
この場合、目的の効果を得るには、最初に Y 軸(この場合はGodotがY軸が上の方向づけを使用するため「上」)に回転を適用する必要があり、次に X 軸で回転します。

最初に X 軸に回転を適用し、次に Y 軸に回転を適用した場合、その効果は望ましくありません:

希望するゲームまたはエフェクトのタイプに応じて、軸の回転を適用する順序が異なる場合があります。したがって、X、Y、Zで回転を適用するだけでは不十分です。回転順序も必要です。
Interpolation(補間)¶
オイラー角の使用に関する別の問題は補間です。 2つの異なるカメラまたは敵の位置(回転を含む)を切り替えたいと想像してください。これにアプローチする1つの論理的な方法は、ある位置から次の位置まで角度を補間することです。次のようになります:

しかし、これは、角度を使用するときに常に期待される効果が得られるわけではありません:

カメラは実際に反対方向に回転しました!
これにはいくつかの理由があります:
回転は方向に対して線形にマッピングされないため、それらを補間しても常に最短パスになるわけではありません(つまり、角度としては
0度と360度は同等ですが、270度から0度に進むことは270度から360度に進むことと同じではありません)。ジンバルロックが発生しています(最初と最後に回転した軸が整列するため、自由度が失われます)。この問題の詳細な説明については、`ウィキペディアのジンバルロックに関するページ <https://en.wikipedia.org/wiki/Gimbal_lock> `_ を参照してください。
オイラー角にノーと言おう¶
このすべての結論は、ゲーム用にGodotの Node3D ノードの rotation プロパティを 使用しない ことです。それは主にエディタで使用され、2Dエンジンとの一貫性、および単純な回転(通常は1軸のみ、または限られた場合は2軸)のために使用されます。誘惑されるかもしれませんが、使用しないでください。
代わりに、回転の問題を解決するより良い方法があります。
transform(変換)の概要¶
Godotは、向きに Transform3D データ型を使用します。各 Node3D ノードには、親がNode3D派生型の場合、親のtransformに関連する transform プロパティが含まれます。
global_transform プロパティを介してワールド座標のtransformにアクセスすることもできます。
transformには Basis (transform.basisサブプロパティ)があり、これは3つの :ref:` class_Vector3` ベクトルで構成されています。これらは transform.basis プロパティを介してアクセスされ、transform.basis.x、transform.basis.y、および transform.basis.z から直接アクセスできます。各ベクトルは、軸が回転した方向を指しているため、ノードの総回転を効果的に表します。スケール(均一である限り)は、軸の長さから推測することもできます。basis は3x3マトリックスとして解釈され、transform.basis[x][y] として使用することもできます。
デフォルトのbasis(変更されていない)は次のようなものです:
var basis = Basis()
# Contains the following default values:
basis.x = Vector3(1, 0, 0) # Vector pointing along the X axis
basis.y = Vector3(0, 1, 0) # Vector pointing along the Y axis
basis.z = Vector3(0, 0, 1) # Vector pointing along the Z axis
// Due to technical limitations on structs in C# the default
// constructor will contain zero values for all fields.
var defaultBasis = new Basis();
GD.Print(defaultBasis); // prints: ((0, 0, 0), (0, 0, 0), (0, 0, 0))
// Instead we can use the Identity property.
var identityBasis = Basis.Identity;
GD.Print(identityBasis.X); // prints: (1, 0, 0)
GD.Print(identityBasis.Y); // prints: (0, 1, 0)
GD.Print(identityBasis.Z); // prints: (0, 0, 1)
// The Identity basis is equivalent to:
var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);
GD.Print(basis); // prints: ((1, 0, 0), (0, 1, 0), (0, 0, 1))
これは3x3単位行列の類似物でもあります。
OpenGLの規則に従って、X は 右 軸、Y は 上 軸、Z は 前方 軸です。
basis と一緒に、transformには origin もあります。これは、このtransformが実際の原点 (0, 0, 0) からどれだけ離れているかを指定する Vector3 です。basis と origin を組み合わせることで、transform は空間内での一意の平行移動、回転、スケールを効率的に表します。
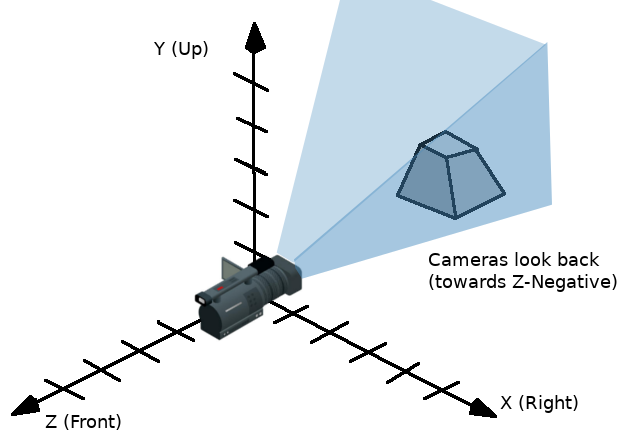
transformを視覚化する1つの方法は、「ローカル空間」モードでオブジェクトの3Dギズモを見ることです。

ギズモの矢印は、basisの X、Y、および Z軸(それぞれ赤、緑、および青)を示し、ギズモの中心はオブジェクトのorigin(原点)にあります。

ベクトルと変換の数学の詳細については、ベクトル演算 チュートリアルをお読みください。
transformの操作¶
もちろん、transformは角度ほど簡単に操作できず、独自の問題があります。
basisを別のbasisに乗算する(これを積算と呼びます)か、回転メソッドを使用して、transformを回転することができます。
var axis = Vector3(1, 0, 0) # Or Vector3.RIGHT
var rotation_amount = 0.1
# Rotate the transform around the X axis by 0.1 radians.
transform.basis = Basis(axis, rotation_amount) * transform.basis
# shortened
transform.basis = transform.basis.rotated(axis, rotation_amount)
Transform3D transform = Transform;
Vector3 axis = new Vector3(1, 0, 0); // Or Vector3.Right
float rotationAmount = 0.1f;
// Rotate the transform around the X axis by 0.1 radians.
transform.Basis = new Basis(axis, rotationAmount) * transform.Basis;
// shortened
transform.Basis = transform.Basis.Rotated(axis, rotationAmount);
Transform = transform;
Node3Dのメソッドはこれを簡素化します:
# Rotate the transform around the X axis by 0.1 radians.
rotate(Vector3(1, 0, 0), 0.1)
# shortened
rotate_x(0.1)
// Rotate the transform around the X axis by 0.1 radians.
Rotate(new Vector3(1, 0, 0), 0.1f);
// shortened
RotateX(0.1f);
これにより、ノードが親ノードに対して相対的に回転します。
オブジェクト空間(ノード独自のtransform)を基準に回転するには、次を使用します:
# Rotate around the object's local X axis by 0.1 radians.
rotate_object_local(Vector3(1, 0, 0), 0.1)
// Rotate around the object's local X axis by 0.1 radians.
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);
精度誤差¶
変換で連続操作を行うと、浮動小数点エラーにより精度が失われます。これは、各軸のスケールがもはや 1.0 ではなく、互いに正確に 90 度ではないことを意味します。
変換がフレームごとに回転すると、最終的には時間の経過とともに変形が始まります。これは避けられません。
これを処理する方法は2つあります。 1つ目は、一定時間後に変換を 正規化 することです(フレームごとに変更する場合は、フレームごとに1回):
transform = transform.orthonormalized()
transform = transform.Orthonormalized();
これにより、すべての軸の長さは再び 1.0 になり、互いに 90 度になります。ただし、transformに適用されたスケールは失われます。
操作するノードをスケーリングしないことをお勧めします。代わりに、子ノードをスケーリングします(MeshInstance3Dなど)。ノードを絶対にスケーリングする必要がある場合は、最後に再適用します:
transform = transform.orthonormalized()
transform = transform.scaled(scale)
transform = transform.Orthonormalized();
transform = transform.Scaled(scale);
情報の取得¶
あなたはこの時点で考えているかもしれません: 「わかりました、しかし、どうすればtransformから角度を取得できますか?」。もう一度答えます: あなたはそうしません。角度で考えるのをやめるために最善を尽くさなければなりません。
プレイヤーが向いている方向に弾丸を撃つ必要があると想像してください。前方軸(通常は Z または -Z)を使用します。
bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED
bullet.Transform = transform;
bullet.LinearVelocity = transform.Basis.Z * BulletSpeed;
敵はプレイヤーを見ていますか?これにはドット積を使用します(ドット積の説明については、 ベクトル演算 チュートリアルを参照してください):
# Get the direction vector from player to enemy
var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
enemy.im_watching_you(player)
// Get the direction vector from player to enemy
Vector3 direction = enemy.Transform.Origin - player.Transform.Origin;
if (direction.Dot(enemy.Transform.Basis.Z) > 0)
{
enemy.ImWatchingYou(player);
}
左に機銃掃射:
# Remember that +X is right
if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)
// Remember that +X is right
if (Input.IsActionPressed("strafe_left"))
{
TranslateObjectLocal(-Transform.Basis.X);
}
ジャンプ:
# Keep in mind Y is up-axis
if Input.is_action_just_pressed("jump"):
velocity.y = JUMP_SPEED
move_and_slide()
// Keep in mind Y is up-axis
if (Input.IsActionJustPressed("jump"))
velocity.Y = JumpSpeed;
MoveAndSlide();
すべての一般的な動作とロジックは、ベクトルだけで実行できます。
設定情報¶
もちろん、情報をtransformに設定したい場合があります。一人称コントローラーまたは周回カメラを想像してください。transformは特定の順序で 実行する必要 があるため、これらは間違いなく角度を使用して行われます。
For such cases, keep the angles and rotations outside the transform and set them every frame. Don't try to retrieve and reuse them because the transform is not meant to be used this way.
FPSスタイルのゲームで見回す例:
# accumulators
var rot_x = 0
var rot_y = 0
func _input(event):
if event is InputEventMouseMotion and event.button_mask & 1:
# modify accumulated mouse rotation
rot_x += event.relative.x * LOOKAROUND_SPEED
rot_y += event.relative.y * LOOKAROUND_SPEED
transform.basis = Basis() # reset rotation
rotate_object_local(Vector3(0, 1, 0), rot_x) # first rotate in Y
rotate_object_local(Vector3(1, 0, 0), rot_y) # then rotate in X
// accumulators
private float _rotationX = 0f;
private float _rotationY = 0f;
public override void _Input(InputEvent @event)
{
if (@event is InputEventMouseMotion mouseMotion)
{
// modify accumulated mouse rotation
_rotationX += mouseMotion.Relative.X * LookAroundSpeed;
_rotationY += mouseMotion.Relative.Y * LookAroundSpeed;
// reset rotation
Transform3D transform = Transform;
transform.Basis = Basis.Identity;
Transform = transform;
RotateObjectLocal(Vector3.Up, _rotationX); // first rotate about Y
RotateObjectLocal(Vector3.Right, _rotationY); // then rotate about X
}
}
ご覧のように、このような場合、回転を外側に保ち、transformを 最終 方向として使用する方が簡単です。
クォータニオンで補間する¶
2つのtransform間の補間は、クォータニオン(四元数)を使用して効率的に実行できます。クォータニオンがどのように機能するかについての詳細は、インターネット周辺の他の場所で見つけることができます。実際の使用のためには、その主な用途のほとんどが最短距離のパス補間を行うことだと理解するだけで十分です。同様に、2つの回転がある場合、クォータニオンにより、最も近い軸を使用したスムーズな補間が可能になります。
回転をクォータニオンに変換するのは簡単です。
# Convert basis to quaternion, keep in mind scale is lost
var a = Quaternion(transform.basis)
var b = Quaternion(transform2.basis)
# Interpolate using spherical-linear interpolation (SLERP).
var c = a.slerp(b,0.5) # find halfway point between a and b
# Apply back
transform.basis = Basis(c)
// Convert basis to quaternion, keep in mind scale is lost
var a = transform.Basis.GetQuaternion();
var b = transform2.Basis.GetQuaternion();
// Interpolate using spherical-linear interpolation (SLERP).
var c = a.Slerp(b, 0.5f); // find halfway point between a and b
// Apply back
transform.Basis = new Basis(c);
Quaternion 型のリファレンスには、データ型に関する詳細な情報があります(transform積算、transformポイントなども可能ですが、使用頻度は低くなります)。クォータニオンに何度も補間または演算を適用する場合は、最終的に正規化する必要があることに注意してください。
クォータニオンは、カメラ/パス/などを行うときに役立ちます。結果は常に正確かつスムーズになります。
Transform(変換)はあなたの友人です¶
ほとんどの初心者にとって、トランスフォームの操作に慣れるには時間がかかる場合があります。ただし、それらに慣れると、そのシンプルさとパワーに感謝します。
Godotの `オンラインコミュニティ <https://godotengine.org/community> `_ でこのトピックに関するヘルプを依頼することを躊躇しないでください。十分に自信が持てたら、次は他の人を助けてください!