Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
ベクトル演算¶
はじめに¶
このチュートリアルは、ゲーム開発に適用される範囲内での、線形代数の短くて実践的な入門書です。線形代数学は、ベクトルとその使い方の研究分野です。2Dおよび3D開発の両方において、ベクトルには多くの応用法があり、Godotではそれらを広範囲で利用しています。すぐれたゲーム開発者になるには、ベクトル数学の十分な理解を深めることが不可欠です。
注釈
このチュートリアルは、線形代数に関する正式な教科書ではありません。それがゲーム開発にどのように適用されるかだけを見ていきます。数学の詳細については、https://www.khanacademy.org/math/linear-algebraを見てください(英語)
座標系 (2D)¶
2D空間では、座標は水平軸 (x) と垂直軸 (y) を使用して定義されます。 2D空間の特定の位置は、(4, 3)などの値のペアとして書き込まれます。
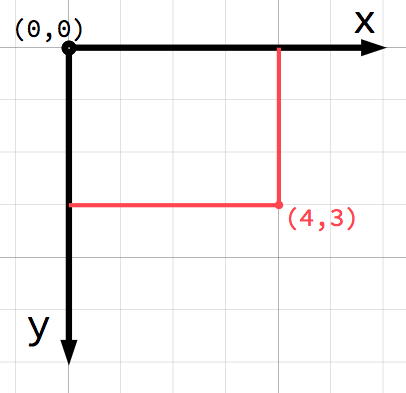
注釈
コンピュータグラフィックスが初めての場合、数学のクラスで学んだように、正の y 軸が上向きではなく 下向き を指すのは奇妙に思えるかもしれません。ただし、これはほとんどのコンピューターグラフィックアプリケーションで一般的です。
この方法で、2D平面内の任意の位置を1組の数字で識別できます。ただし、位置 (4, 3) は (0, 0) ポイントまたは原点からの オフセット と考えることもできます。原点 からポイントを指す矢印を描画します:
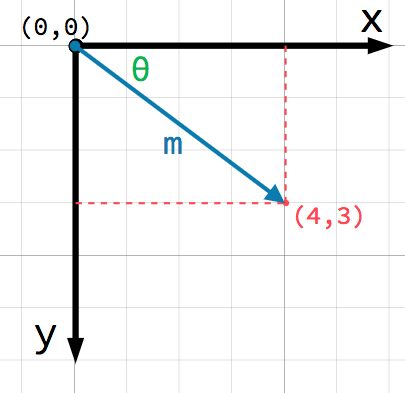
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
ベクトルについて考慮すべき非常に重要な点は、ベクトルが 相対的 な方向と大きさのみを表すことです。ベクトルのには位置の概念はありません。次の2つのベクトルは同一です:
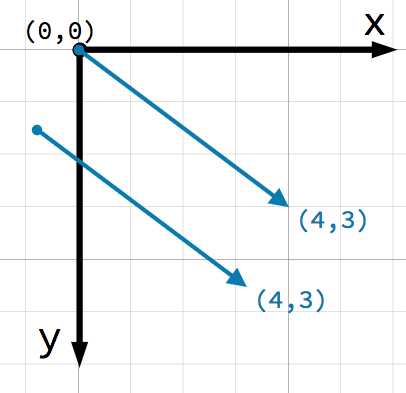
両方のベクトルは、開始点から右に4単位、下に3単位の点を表します。平面上のどこでベクトルを描くかは問題ではなく、常に相対的な方向と大きさを表します。
ベクトル操作¶
いずれかの方法(xおよびy座標または角度と大きさ)を使用してもベクトルを参照できますが、プログラマーは通常、座標表記を使用します。たとえば、Godotでは、原点は画面の左上隅であるため、Node2D という名前の2Dノードを右に400ピクセル、下に300ピクセル配置するには、次のコードを使用します:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
メンバアクセス¶
ベクトルの個々のコンポーネントには、名前で直接アクセスできます。
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
ベクトルの加算¶
2つのベクトルを加算または減算すると、対応するコンポーネントが追加されます:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
また、最初のベクトルの終点に2番目のベクトルを追加することで、これを視覚的に確認できます:
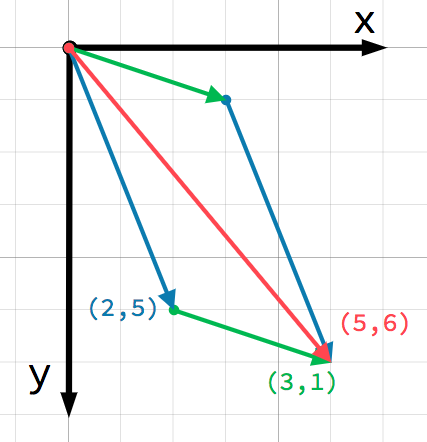
a + b は、b + a と同じ結果になることに注意してください。
スカラー乗算¶
注釈
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
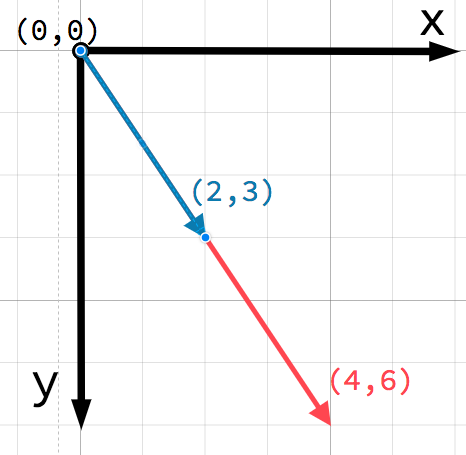
ベクトルには スカラー を掛けることができます:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
注釈
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
実際の応用¶
ベクトルの加算と減算の2つの一般的な使用方法を見てみましょう。
移動¶
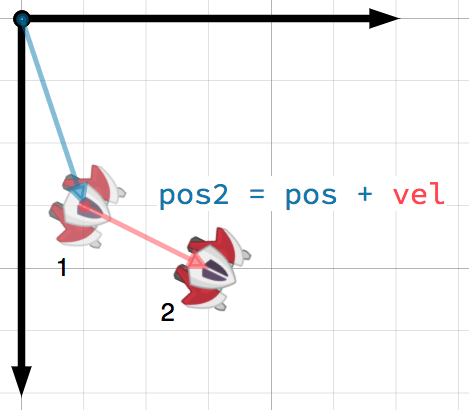
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
ちなみに
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
ターゲットへ向く¶
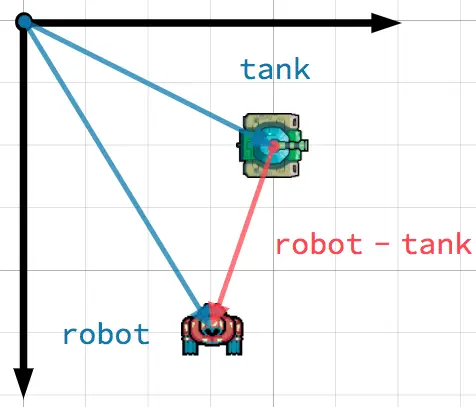
このシナリオでは、砲塔をロボットに向けたい戦車があります。ロボットの位置からタンクの位置を引くと、タンクからロボットを指すベクトルが得られます。
ちなみに
To find a vector pointing from A to B, use B - A.
単位ベクトル¶
大きさが1のベクトルを、単位ベクトルと呼びます。また、方向ベクトルまたは法線と呼ばれることもあります。単位ベクトルは、方向を追跡する必要がある場合に役立ちます。
正規化¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
警告
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
反射¶
単位ベクトルの一般的な用途は、法線を示すことです。法線ベクトルは、面の表面に垂直に配置され、その方向を定義する単位ベクトルです。これらは一般に、照明、衝突、およびサーフェスに関連する他の操作に使用されます。
例として、動いているボールを想像してみましょう。壁や他の物体に当たったら跳ね返ってほしいですね:
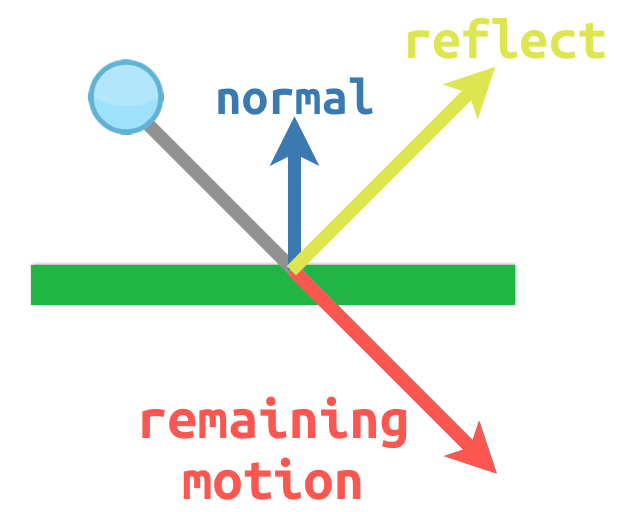
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
内積 (ドット積)¶
内積は、ベクトル数学の最も重要な概念の1つですが、誤解されることがよくあります。内積は、2つのベクトルを演算してスカラーを返します。大きさと方向の両方を含むベクトルとは異なり、スカラーは大きさのみを持ちます。
内積の式には、2つの一般的な形式があります:
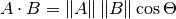
そして
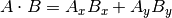
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
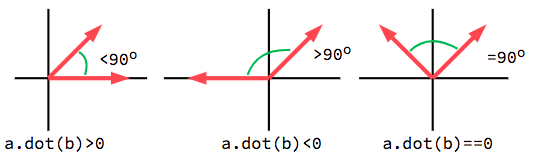
単位ベクトルを利用すると結果は -1 (180°)から 1 (0°)になります。
正面¶
これを利用して、オブジェクトが別のオブジェクトに向いているかどうかを検出できます。下の図では、プレイヤー P はゾンビ A と B を避けようとしています。ゾンビの視界が 180度 であると仮定すると、ゾンビはプレイヤーを見ることができるでしょうか?
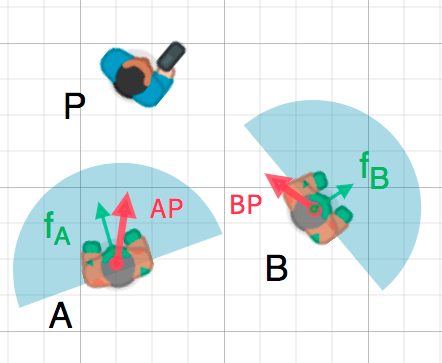
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
コードでは次のように表せます:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
外積 (クロス積)¶
内積と同様に、外積は2つのベクトルの演算です。ただし、外積の結果は、両方に垂直な方向を持つベクトルです。その大きさは、相対的な角度に依存します。 2つのベクトルが平行である場合、それらの外積の結果はヌルベクトルになります。

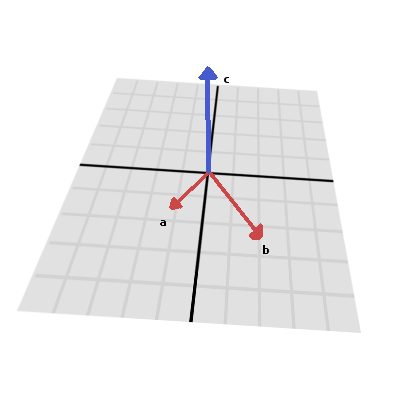
外積は以下のように求めます:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
注釈
外積では、順序が重要です。a.cross(b)はb.cross(a)と同じ結果にはなりません。結果のベクトルは反対方向を指します。
法線の計算¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
三角形の法線を計算する関数は以下のとおりです:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
ターゲットへの方向¶
上記の内積セクションでは、2つのベクトル間の角度を見つけるためにそれをどのように使用できるかを見ました。ただし、3Dでは、これは十分な情報ではありません。さらに、どの軸を中心に回転するかを知る必要があります。これは、現在の向きとターゲットの方向の外積を計算することでわかります。結果の垂直ベクトルが回転の軸です。
より多くの情報¶
Godotでのベクトル演算の使用の詳細については、次の記事を参照してください: