Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
ベジェ、曲線、パス¶
ベジェ曲線は、自然な幾何学的形状の数学的な近似です。これらを使用して、可能な限り少ない情報と高いレベルの柔軟性で曲線を表します。
より抽象的な数学的概念とは異なり、ベジェ曲線は工業デザイン用に作成されました。これらは、グラフィックソフトウェア業界で人気のあるツールです。
前の記事で見た interpolation に依存し、複数のステップを組み合わせて滑らかな曲線を作成します。ベジェ曲線がどのように機能するかをよりよく理解するために、最も単純な形式である二次ベジェから始めましょう。
二次ベジェ¶
二次ベジェが機能するために最低限必要な3つのポイントを用意します:
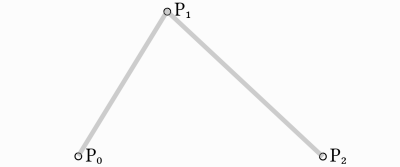
それらの間に曲線を描くために、最初に3つのポイントによって形成される2つのセグメントのそれぞれの2つの頂点を0〜1の範囲の値を使用して徐々に補間します。これにより、t の値を0から1に変更すると、セグメントに沿って移動する2つのポイントが得られます。
func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
}
次に、q0 と q1 を補間して、曲線に沿って移動する単一のポイント r を取得します。
var r = q0.lerp(q1, t)
return r
Vector2 r = q0.Lerp(q1, t);
return r;
This type of curve is called a Quadratic Bezier curve.
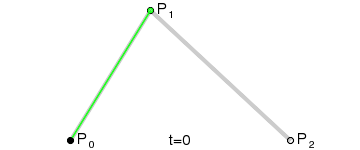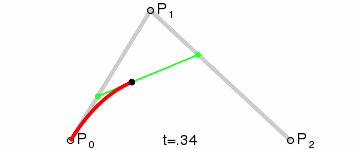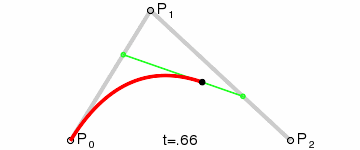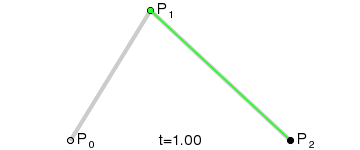
(画像クレジット: Wikipedia)
三次(立方)ベジェ¶
前の例に基づいて、4つのポイント間を補間することで、より詳細な制御を得ることができます。
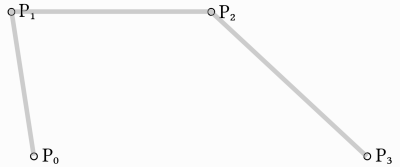
まず、4つのパラメーターを持つ関数を使用して、入力として p0、p1、p2、および ``p3``の4つのポイントを取得します:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
}
ポイントの各カップルに線形補間を適用して、それらを3つに減らします:
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
次に、3つのポイントを取り、それらを2つに減らします:
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
そして1つに:
var s = r0.lerp(r1, t)
return s
Vector2 s = r0.Lerp(r1, t);
return s;
完全な関数は次のとおりです:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
var s = r0.lerp(r1, t)
return s
private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Vector2 s = r0.Lerp(r1, t);
return s;
}
結果は、4つのポイントすべてを補間する滑らかな曲線になります:
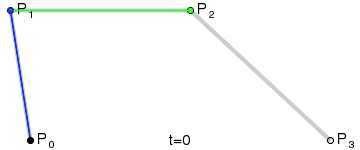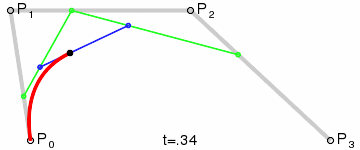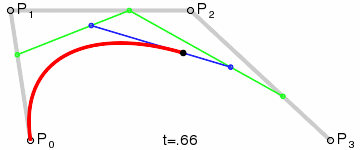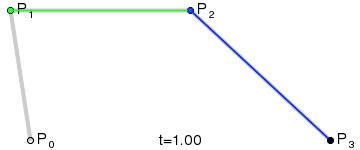
(画像クレジット: Wikipedia)
注釈
三次ベジェ補間は3Dでも同じように機能し、Vector2 ではなく Vector3 を使用します。
コントロールポイントの追加¶
三次ベジェに基づいて、2つのポイントの動作方法を変更して、曲線の形状を自由に制御できます。p0、p1、p2、および ``p3``の代わりに、次のように保存します:
point0 = p0: 最初のポイント、ソースcontrol0 = p1 - p0: 最初の制御点の相対的なベクトルcontrol1 = p3 - p2: 2番目の制御点の相対的なベクトルpoint1 = p3: 2番目のポイント、目的地
このように、2つのポイントと、それぞれのポイントに相対的なベクトルである2つのコントロールポイントがあります。グラフィックまたはアニメーションソフトウェアを以前に使用したことがある場合、これはおなじみのように見えるかもしれません:
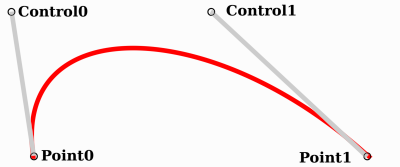
グラフィックス ソフトウェアがユーザーにベジエ曲線を提示する方法と、それらがどのように動作し、Godot でどのように見えるかです。
Curve2D、Curve3D、PathおよびPath2D¶
曲線を含む2つのオブジェクトがあります: Curve3D および :ref:`Curve2D <class_Curve2D>`(それぞれ3Dおよび2D用)。
They can contain several points, allowing for longer paths. It is also possible to set them to nodes: Path3D and Path2D (also for 3D and 2D respectively):
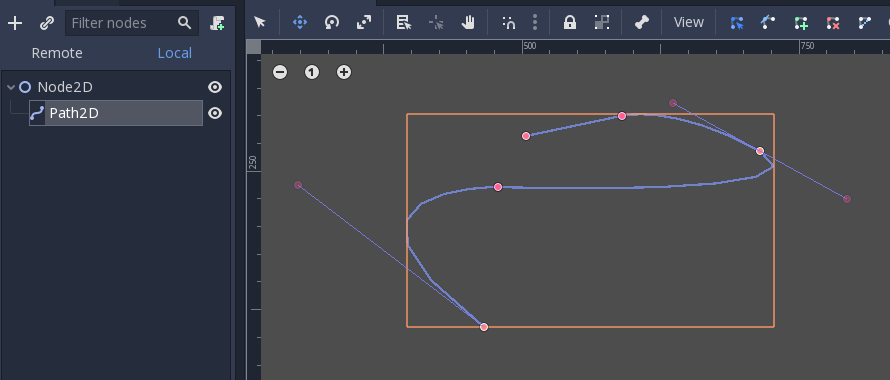
ただし、それらを使用することは完全に明白ではない可能性があるため、以下ではベジェ曲線の最も一般的な使用例について説明します。
評価する¶
Only evaluating them may be an option, but in most cases it's not very useful. The big drawback with Bezier curves is that if you traverse them at constant speed, from t = 0 to t = 1, the actual interpolation will not move at constant speed. The speed is also an interpolation between the distances between points p0, p1, p2 and p3 and there is not a mathematically simple way to traverse the curve at constant speed.
Let's do an example with the following pseudocode:
var t = 0.0
func _process(delta):
t += delta
position = _cubic_bezier(p0, p1, p2, p3, t)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = CubicBezier(p0, p1, p2, p3, _t);
}

ご覧のとおり、t は一定の速度で増加しますが、円の速度(ピクセル/秒)は変化します。これにより、実用的なものにベジェを「箱から出したままで」使用することが難しくなります。
描画¶
ベジェ(または曲線に基づくオブジェクト)の描画は非常に一般的な使用例ですが、簡単ではありません。ほとんどの場合、ベジェ曲線は何らかの種類のセグメントに変換する必要があります。ですが、これは通常、非常に多くの量は作成できす困難です。
その理由は、曲線の一部のセクション(具体的にはコーナー)にはかなりの量のポイントが必要な場合がありますが、他のセクションには必要ない場合があるためです:

さらに、両方のコントロールポイントが 0, 0 (それらが相対ベクトルであることを思い出してください)の場合、ベジェ曲線は単なる直線になります(したがって、大量のポイントを描画すると無駄になります)。
ベジェ曲線を描く前に、テセレーションが必要です。これは、多くの場合、湾曲量が特定のしきい値より小さくなるまで曲線を分割する再帰的関数または分割統治関数で行われます。
*Curve * クラスは、これを Curve2D.tessellate() 関数(再帰と角度 tolerance 引数のオプションの stage を受け取る)を介して提供します。この方法では、曲線に基づいて何かを描くのが簡単です。
トラバーサル¶
曲線の最後の一般的な使用例は、曲線をトラバースすることです。一定の速度に関して以前に言及されたことのため、これも困難です。
To make this easier, the curves need to be baked into equidistant points. This way, they can be approximated with regular interpolation (which can be improved further with a cubic option). To do this, just use the Curve3D.sample_baked() method together with Curve2D.get_baked_length(). The first call to either of them will bake the curve internally.
一定の速度でのトラバースは、次の擬似コードで実行できます:
var t = 0.0
func _process(delta):
t += delta
position = curve.sample_baked(t * curve.get_baked_length(), true)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}
そして、出力は一定の速度で動きます:
