Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Использование 3D-преобразований¶
Введение¶
Если вы никогда раньше не делали 3D-игр, то работа с вращением в трёх измерениях может сначала сбить с толку. Выходя из 2D, естественный образ мышления лежит по линии "О, это как вращение в 2D, за исключением того, что теперь вращения происходят в X, Y и Z ".
Поначалу это кажется простым. Для простых игр такого образа мышления может быть даже достаточно. К сожалению, зачастую это неверно.
Углы в трёх измерениях чаще всего называют «углами Эйлера».
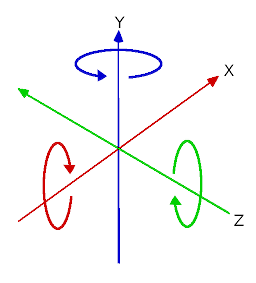
Углы Эйлера были описаны математиком Леонардом Эйлером в начале 1700-х годов.

Такой способ представления трехмерных вращений был новаторским в то время, но у него есть несколько недостатков при использовании в разработке игр (чего и следовало ожидать от парня в забавной шляпе). Идея этого документа состоит в том, чтобы объяснить почему, а также в общих чертах изложить передовые методы работы с преобразованиями при программировании 3D-игр.
Проблемы углов Эйлера¶
Хотя может показаться интуитивно понятным, что каждая ось вращается, на самом деле это просто непрактично.
Порядок осей координат¶
Основная причина этого в том, что не существует уникального способа построения ориентации по углам. Не существует стандартной математической функции, которая складывала бы все углы вместе и производила бы фактическое трехмерное вращение. Единственный способ получить ориентацию по углам - это повернуть объект на угол в произвольном порядке.
Это можно сделать, сначала повернув X, затем Y, а затем Z. В качестве альтернативы вы можете сначала повернуть по Y, затем по Z и, наконец, по X. Все работает, но в зависимости от порядка окончательная ориентация объекта не обязательно будет одинаковой. Это означает, что есть несколько способов построить ориентацию с 3 разных углов, в зависимости от порядка поворотов.
Ниже представлена визуализация осей вращения (в порядке X, Y, Z) в подвесе (из Википедии). Как видите, ориентация каждой оси зависит от поворота предыдущей:
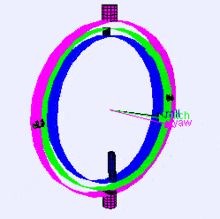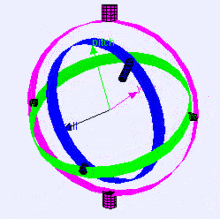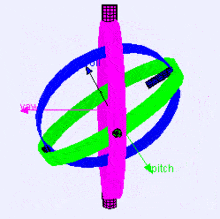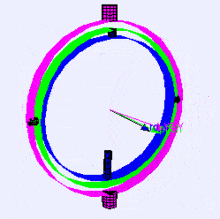
Вам может быть интересно, как это на вас влияет. Давайте посмотрим на практический пример:
Представьте, что вы работаете над контроллером от первого лица (например, над игрой FPS). Перемещение мыши влево и вправо управляет углом обзора параллельно земле, а перемещение её вверх и вниз перемещает взгляд игрока вверх и вниз.
В этом случае для достижения желаемого эффекта сначала необходимо применить вращение по оси Y (в данном случае "вверх", поскольку Godot использует ориентацию "Y-вверх"), а затем - по оси X.

Если бы мы сначала применили вращение по оси X, а затем по Y, эффект был бы нежелательным:

В зависимости от типа игры или желаемого эффекта порядок, в котором вы хотите применить вращение оси, может отличаться. Следовательно, применения вращения по осям X, Y и Z недостаточно: вам также понадобится порядок вращения.
Интерполяция¶
Еще одна проблема с использованием углов Эйлера - интерполяция. Представьте, что вы хотите переключаться между двумя разными позициями камеры или врага (включая поворот). Один из логических способов приблизиться к этому - интерполировать углы от одного положения к другому. Можно было бы ожидать, что это будет выглядеть так:

Но это не всегда дает ожидаемый эффект при использовании углов:

На самом деле камера вращалась в противоположном направлении!
Это может произойти по нескольким причинам:
Повороты не отображаются линейно на ориентацию, поэтому их интерполяция не всегда приводит к кратчайшему пути (т.е. Переход от
270к0градусов - не то же самое, что переход от270к360, даже если углы эквивалентны).Блокировка подвеса (первая и последняя повернутые оси совпадают, поэтому степень свободы теряется). См. страницу Википедии о Gimbal Lock для подробного объяснения этой проблемы.
Скажи нет углам Эйлера¶
The result of all this is that you should not use the rotation property of Node3D nodes in Godot for games. It's there to be used mainly in the editor, for coherence with the 2D engine, and for simple rotations (generally just one axis, or even two in limited cases). As much as you may be tempted, don't use it.
Есть более удобный способ решения проблемы с поворотом.
Введение в трансформации¶
Godot uses the Transform3D datatype for orientations. Each Node3D node contains a transform property which is relative to the parent's transform, if the parent is a Node3D-derived type.
Также возможно получить доступ к трансформациям в мировых координатах через свойство global_transform.
Преобразование имеет Basis (подсвойство transform.basis), которое состоит из трех векторов Vector3. К ним можно получить доступ через свойство transform.basis, либо напрямую к каждой оси через transform.basis.x, transform.basis.y и transform.basis.z. Каждый вектор указывает направление вращения его оси, поэтому они эффективно описывают полное вращение узла. Масштаб (если он однородный) также можно определить по длине осей. Базис также можно интерпретировать как матрицу 3x3 и использовать как transform.basis[x][y].
Базис по умолчанию (без изменений) похож на:
var basis = Basis()
# Contains the following default values:
basis.x = Vector3(1, 0, 0) # Vector pointing along the X axis
basis.y = Vector3(0, 1, 0) # Vector pointing along the Y axis
basis.z = Vector3(0, 0, 1) # Vector pointing along the Z axis
// Due to technical limitations on structs in C# the default
// constructor will contain zero values for all fields.
var defaultBasis = new Basis();
GD.Print(defaultBasis); // prints: ((0, 0, 0), (0, 0, 0), (0, 0, 0))
// Instead we can use the Identity property.
var identityBasis = Basis.Identity;
GD.Print(identityBasis.X); // prints: (1, 0, 0)
GD.Print(identityBasis.Y); // prints: (0, 1, 0)
GD.Print(identityBasis.Z); // prints: (0, 0, 1)
// The Identity basis is equivalent to:
var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);
GD.Print(basis); // prints: ((1, 0, 0), (0, 1, 0), (0, 0, 1))
Это также аналог единичной матрицы 3x3.
По соглашениям, принятым в OpenGL, X - это ось вправо, Y - ось вверх, а Z - ось вперёд.
Вместе с базисом преобразование также имеет точку опоры. Это Vector3, определяющий, насколько далеко от фактической точки опоры (0, 0, 0) находится это преобразование. Комбинируя базис с точкой опоры, преобразование эффективно представляет собой уникальный перенос, поворот и масштаб в пространстве.
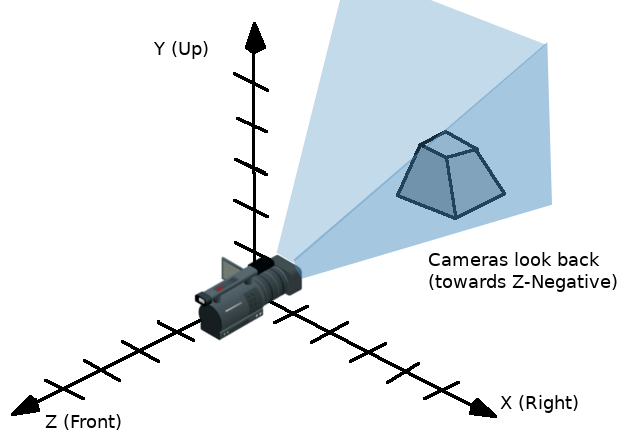
Один из способов визуализировать преобразование - это посмотреть на трехмерный гизмо объекта в режиме "локального пространства".

Стрелки гизмо показывают оси X, Y и Z (красным, зелёным и синим цветом соответственно) основы, а центр гизмо находится в точке опоры объекта.

Для получения дополнительной информации о математике векторов и преобразований, пожалуйста, прочтите руководства Векторная математика.
Управление преобразованиями¶
Конечно, преобразованиями не так просто манипулировать, как углами, и у них есть свои собственные проблемы.
Можно повернуть преобразование либо путем умножения его базиса на другой (это называется накоплением), либо с помощью методов поворота.
var axis = Vector3(1, 0, 0) # Or Vector3.RIGHT
var rotation_amount = 0.1
# Rotate the transform around the X axis by 0.1 radians.
transform.basis = Basis(axis, rotation_amount) * transform.basis
# shortened
transform.basis = transform.basis.rotated(axis, rotation_amount)
Transform3D transform = Transform;
Vector3 axis = new Vector3(1, 0, 0); // Or Vector3.Right
float rotationAmount = 0.1f;
// Rotate the transform around the X axis by 0.1 radians.
transform.Basis = new Basis(axis, rotationAmount) * transform.Basis;
// shortened
transform.Basis = transform.Basis.Rotated(axis, rotationAmount);
Transform = transform;
A method in Node3D simplifies this:
# Rotate the transform around the X axis by 0.1 radians.
rotate(Vector3(1, 0, 0), 0.1)
# shortened
rotate_x(0.1)
// Rotate the transform around the X axis by 0.1 radians.
Rotate(new Vector3(1, 0, 0), 0.1f);
// shortened
RotateX(0.1f);
Таким образом поворачивается узел относительно родительского узла.
Для поворота относительно пространства объекта (собственное преобразование узла) используйте следующее:
# Rotate around the object's local X axis by 0.1 radians.
rotate_object_local(Vector3(1, 0, 0), 0.1)
// Rotate around the object's local X axis by 0.1 radians.
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);
Ошибки точности¶
Выполнение последовательных операций с преобразованиями приведет к потере точности из-за ошибок вычислений с плавающей запятой. Это означает, что масштаб каждой оси больше не может быть строго 1.0, и они могут не быть повёрнуты строго на 90 градусов относительно друг от друга.
Если поворот осуществляется каждый кадр, со временем накапливается ошибка точности. Это неизбежно.
Есть два разных способа справиться с этим. Первый - ортонормировать преобразование через некоторое время (возможно, один раз за кадр, если вы изменяете его каждый кадр):
transform = transform.orthonormalized()
transform = transform.Orthonormalized();
В результате все оси снова будут иметь длину 1.0 и будут повёрнуты на 90 градусов друг относительно друга. Однако любой масштаб, примененный к преобразованию, будет утерян.
It is recommended you not scale nodes that are going to be manipulated; scale their children nodes instead (such as MeshInstance3D). If you absolutely must scale the node, then re-apply it at the end:
transform = transform.orthonormalized()
transform = transform.scaled(scale)
transform = transform.Orthonormalized();
transform = transform.Scaled(scale);
Получение информации¶
В этот момент вы можете подумать: "Хорошо, но как мне получить углы при трансформации?". И снова ответ: вам это не нужно. Вы должны любыми способами избегать мыслей об углах.
Представьте, что вам нужно выстрелить в направлении, в котором смотрит ваш игрок. Просто используйте ось, направленную вперёд (обычно Z или -Z).
bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED
bullet.Transform = transform;
bullet.LinearVelocity = transform.Basis.Z * BulletSpeed;
Враг смотрит на игрока? Используйте для этого скалярное произведение (см. Руководство Векторная математика для объяснения скалярного произведения):
# Get the direction vector from player to enemy
var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
enemy.im_watching_you(player)
// Get the direction vector from player to enemy
Vector3 direction = enemy.Transform.Origin - player.Transform.Origin;
if (direction.Dot(enemy.Transform.Basis.Z) > 0)
{
enemy.ImWatchingYou(player);
}
Атака слева:
# Remember that +X is right
if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)
// Remember that +X is right
if (Input.IsActionPressed("strafe_left"))
{
TranslateObjectLocal(-Transform.Basis.X);
}
Прыжок:
# Keep in mind Y is up-axis
if Input.is_action_just_pressed("jump"):
velocity.y = JUMP_SPEED
move_and_slide()
// Keep in mind Y is up-axis
if (Input.IsActionJustPressed("jump"))
velocity.Y = JumpSpeed;
MoveAndSlide();
Всё обычное поведение и логику можно реализовать с помощью одних только векторов.
Установка информации¶
Конечно, есть случаи, когда вы хотите установить информацию для преобразования. Представьте себе контроллер от первого лица или движущуюся по орбите камеру. Это определенно делается с использованием углов, потому что вы действительно хотите, чтобы преобразования происходили в определенном порядке.
For such cases, keep the angles and rotations outside the transform and set them every frame. Don't try to retrieve and reuse them because the transform is not meant to be used this way.
Пример осмотра вокруг в стиле FPS:
# accumulators
var rot_x = 0
var rot_y = 0
func _input(event):
if event is InputEventMouseMotion and event.button_mask & 1:
# modify accumulated mouse rotation
rot_x += event.relative.x * LOOKAROUND_SPEED
rot_y += event.relative.y * LOOKAROUND_SPEED
transform.basis = Basis() # reset rotation
rotate_object_local(Vector3(0, 1, 0), rot_x) # first rotate in Y
rotate_object_local(Vector3(1, 0, 0), rot_y) # then rotate in X
// accumulators
private float _rotationX = 0f;
private float _rotationY = 0f;
public override void _Input(InputEvent @event)
{
if (@event is InputEventMouseMotion mouseMotion)
{
// modify accumulated mouse rotation
_rotationX += mouseMotion.Relative.X * LookAroundSpeed;
_rotationY += mouseMotion.Relative.Y * LookAroundSpeed;
// reset rotation
Transform3D transform = Transform;
transform.Basis = Basis.Identity;
Transform = transform;
RotateObjectLocal(Vector3.Up, _rotationX); // first rotate about Y
RotateObjectLocal(Vector3.Right, _rotationY); // then rotate about X
}
}
Как видите, в таких случаях ещё проще сохранить вращение снаружи, а затем использовать преобразование в качестве окончательной ориентации.
Интерполяция с кватернионами¶
Интерполяция между двумя преобразованиями может эффективно выполняться с помощью кватернионов. Более подробную информацию о том, как работают кватернионы, можно найти в других местах в Интернете. Для практического использования достаточно понять, что в основном они используются для интерполяции кратчайшего пути. Например, если у вас есть два поворота, кватернион плавно выполнит интерполяцию между ними с использованием ближайшей оси.
Преобразовать вращение в кватернион несложно.
# Convert basis to quaternion, keep in mind scale is lost
var a = Quaternion(transform.basis)
var b = Quaternion(transform2.basis)
# Interpolate using spherical-linear interpolation (SLERP).
var c = a.slerp(b,0.5) # find halfway point between a and b
# Apply back
transform.basis = Basis(c)
// Convert basis to quaternion, keep in mind scale is lost
var a = transform.Basis.GetQuaternion();
var b = transform2.Basis.GetQuaternion();
// Interpolate using spherical-linear interpolation (SLERP).
var c = a.Slerp(b, 0.5f); // find halfway point between a and b
// Apply back
transform.Basis = new Basis(c);
The Quaternion type reference has more information on the datatype (it can also do transform accumulation, transform points, etc., though this is used less often). If you interpolate or apply operations to quaternions many times, keep in mind they need to be eventually normalized. Otherwise, they will also suffer from numerical precision errors.
Кватернионы полезны при выполнении интерполяции камеры, пути и т.д., так как результат всегда будет правильным и плавным.
Трансформации - твои друзья¶
Для большинства новичков привыкание к работе с преобразованиями может занять некоторое время. Однако, как только вы к ним привыкнете, вы оцените их простоту и мощность.
Не стесняйтесь обращаться за помощью по этой теме в любое из онлайн-сообществ Godot и, как только вы станете достаточно уверенными в теме, пожалуйста, помогите другим!