Використання 3D перетворень¶
Вступ¶
Якщо ви досі ніколи не розробляли 3D ігор, то обертання у трьох вимірах, спершу, може вам здатись незрозумілим. Після 2D вам може здатись: „О! Це прямо як в 2D, але з додатковими осями!“.
Спочатку це здається легким. Для простих ігор такого способу мислення може бути навіть достатньо. Але, на жаль, це враження зазвичай оманливе.
Кути у три-вимірному просторі найчастіше називають "Кутами Ейлера".
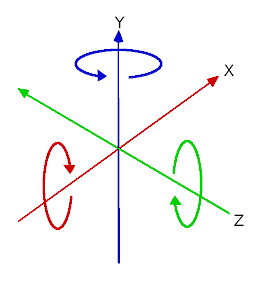
Кути Ейлера були описані математиком Леонардом Ейлером на початку 18ст.
Такий підхід до опису 3D орієнтації був проривним для свого часу, але він має декілька недоліків коли використовується при розробці ігор (чого ще очікувати від чоловіка у смішному капелюсі). Ця стаття покликана пояснити чому так, а також описати найкращі шляхи роботи з перетвореннями 3D об'єктів.
Проблеми кутів Ейлера¶
Хоча й здається, що об'єкт можна просто обертати навколо кожної з осей, на ділі це практично.
Порядок осей¶
Головна причина цього в тому, що не існує єдиного способу отримати орієнтацію з кутів. Немає стандартної математичної функції, яка приймає всі кути й повертає реальне положення об'єкта. Єдиний спосіб отримати це положення — обертати об'єкт за цими кутами в певному порядку.
Це можна зробити, покрутивши об'єкт спершу по осі X, потім — по Y і потім — по Z. Або ж, ви можете спершу покрутити по осі Y, а потім — по Z і нарешті — по X. Будь-який спосіб підходить, але кінцевий результат не обов'язково буде однаковим. А значить — існує декілька способів знаходження обертання за трьома кутами, залежно від порядку обертань.
Нижче наведене зображення осей обертання (в порядку X, Y, Z) у вигляді карданного підвісу (з Вікіпедії). Як бачите, положення кожної з осей залежить від повороту попередньої осі:
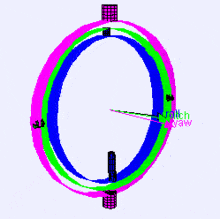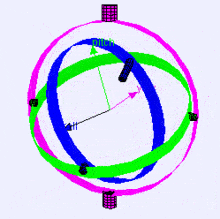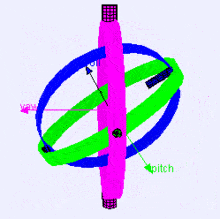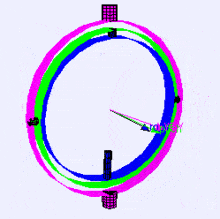
У вас може виникнути питання: „Як це може вплинути на мене?“. Погляньмо на приклад з практики:
Уявіть, що ви працюєте над управлінням від першої особи (як в шутерах). Рух курсора в ліво-право повинен контролювати той кут огляду, що паралельний до землі. Натомість, рухаючи курсор вгору й вниз гравець переміщує свій огляд відповідно вгору та вниз.
В такому разі, щоб досягти необхідного результату, обертати спершу потрібно вісь Y (в нашому випадку вісь „вгору“, так як Godot використовує орієнтацію „Y-Up“), а потім — вісь X.
Якби ми спершу повернули вісь X, а потім — Y, то ми отримали б небажаний результат:
Залежно від типу гри й результату, якого ви хочете досягти, порядок, в якому потрібно обертати об'єкт, може відрізнятись. Тому, застосовувати обертання в порядку X, Y, Z не достатньо: потрібно також знати й порядок обертання.
Інтерполяція¶
Ще одна проблема, яка виникає при роботі з кутами Ейлера — це інтерполяція. Уявіть, що ви хочете зробити плавний перехід між двома різними камерами чи положеннями ворогів (включно з їх орієнтаціями). Найпростіший спосіб — інтерполювати значення кута по кожній з осей незалежно. Отриманий результат повинен бути ось таким:
Але кути не завжди працюють так, як повинні:
Насправді, камера крутиться у протилежний бік!
Є декілька причин, чому могло так трапитись:
Обертання не були лінійно прив'язані до орієнтації, а тому інтерполяція не завжди обирає найкоротший шлях (як-от шлях від
270до0градусів — це не те ж саме що шлях від270до360хоч це й однакові кути).Сталось блокування обертання (перша вісь обертання вирівнялась з останньою й система втратила одну степінь свободи). Подивіться статтю по блокування обертання <https://uk.wikipedia.org/wiki/Блокування_обертання>` _ якщо хочете дізнатися більше.
Скажіть „Ні“ кутам Ейлера¶
Виходячи з усього вище сказаного, вам не варто використовувати властивість rotation вузла Spatial у своїх іграх. Вони призначені для використання в редакторі, для відповідності з 2D рушієм. А також для простих обертань (зазвичай по одній осі, рідше — по двох). Тому, як би сильно вам не хотілось, не використовуйте його.
Натомість, існує кращий спосіб вирішити проблему обертання.
Знайомство з перетвореннями¶
Godot використовує тип Transform для опису орієнтації. Кожен вузол типу Spatial має властивість transform яка описує його положення відносно батьківського вузла, в тому разі, якщо батьківський вузол належить до класу, що походить від Spatial.
Також, можна отримати глобальне положення об'єкта у властивості global_transform.
Перетворення має базис Basis (підвластивість transform.basis), який складається з трьох векторів ref:class_Vector3. Доступ до них можна отримати через властивість transform.basis і напряму, через transform.basis.x, transform.basis.y, and transform.basis.z. Кожен з векторів напрямлений так само, як і його вісь після обертання, таким чином описуючи сумарний поворот об'єкта. Масштабування ж (якщо воно рівномірне) можна визначити з довжин осей. Базис також можна описати як матрицю 3x3 та використовувати як transform.basis[x][y].
Початковий базис (незмінений) виглядає десь так:
var basis = Basis()
# Contains the following default values:
basis.x = Vector3(1, 0, 0) # Vector pointing along the X axis
basis.y = Vector3(0, 1, 0) # Vector pointing along the Y axis
basis.z = Vector3(0, 0, 1) # Vector pointing along the Z axis
// Due to technical limitations on structs in C# the default
// constructor will contain zero values for all fields.
var defaultBasis = new Basis();
GD.Print(defaultBasis); // prints: ((0, 0, 0), (0, 0, 0), (0, 0, 0))
// Instead we can use the Identity property.
var identityBasis = Basis.Identity;
GD.Print(identityBasis.x); // prints: (1, 0, 0)
GD.Print(identityBasis.y); // prints: (0, 1, 0)
GD.Print(identityBasis.z); // prints: (0, 0, 1)
// The Identity basis is equivalent to:
var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);
GD.Print(basis); // prints: ((1, 0, 0), (0, 1, 0), (0, 0, 1))
Також він являється аналогом одиничної матриці 3x3.
Відповідно до стандарту OpenGL, X це Права вісь, Y — це вісь Вгору й Z — це вісь Уперед.
Разом з базисом перетворення також має початкову точку. Це Vector3 який описує як далеко об'єкт знаходиться від початку координат (0, 0, 0). З базисом та початковою точкою, перетворення повністю описує переміщення, обертання та масштабування у просторі.
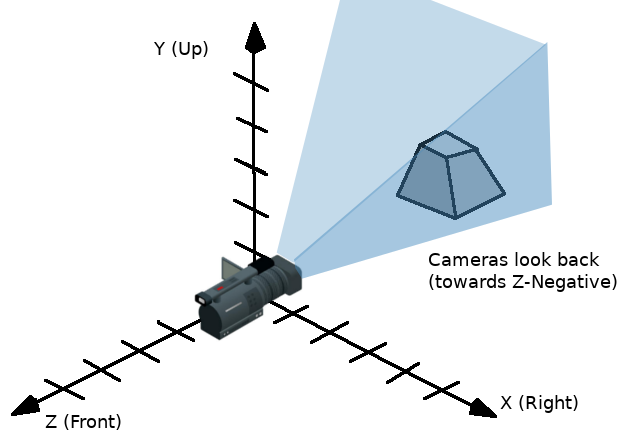
Щоб побачити, як працюють перетворення можна поглянути на 3D ґізмо об'єкта, перемкнуте в режим локального простору.
Стрілочки на ґізмо вказують на осі базису X, Y і Z (червоного, зеленого та синього кольорів відповідно). А центр же ґізмо вказує на початкову точку об'єкта.
Якщо хочете дізнатись більше про векторну математику та перетворення, прочитайте статтю Векторна математика.
Використання перетворень¶
Звісно, використовувати перетворення не так просто як кути. Та й свої проблеми вони також мають.
Повернути об'єкт можна перемноживши базис його перетворення на базис іншого (це називається композицією) або використавши методи обертання.
var axis = Vector3(1, 0, 0) # Or Vector3.RIGHT
var rotation_amount = 0.1
# Rotate the transform around the X axis by 0.1 radians.
transform.basis = Basis(axis, rotation_amount) * transform.basis
# shortened
transform.basis = transform.basis.rotated(axis, rotation_amount)
Vector3 axis = new Vector3(1, 0, 0); // Or Vector3.Right
float rotationAmount = 0.1f;
// Rotate the transform around the X axis by 0.1 radians.
transform.basis = new Basis(axis, rotationAmount) * transform.basis;
// shortened
transform.basis = transform.basis.Rotated(axis, rotationAmount);
Метод у Spatial спрощує це:
# Rotate the transform around the X axis by 0.1 radians.
rotate(Vector3(1, 0, 0), 0.1)
# shortened
rotate_x(0.1)
// Rotate the transform around the X axis by 0.1 radians.
Rotate(new Vector3(1, 0, 0), 0.1f);
// shortened
RotateX(0.1f);
Він обертає вузол відносно батьківського вузла.
Щоб обертатись відносно власного простору об'єкта потрібно використати наступний код:
# Rotate around the object's local X axis by 0.1 radians.
rotate_object_local(Vector3(1, 0, 0), 0.1)
// Rotate around the object's local X axis by 0.1 radians.
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);
Помилки пов'язані з точністю¶
Виконання перетворень, з часом, спричиняє втрату точності у зв'язку з обмеженнями чисел з рухомою комою. Через це, довжини осей можуть не дорівнювати точно 1.0 та кути між ними можуть не дорівнювати точно 90 градусів.
Якщо перетворення відбуваються в кожному кадрі, то вони в решті-решт почнуть деформуватись. Уникнути цього неможливо.
Існують два способи справитись з цим. Перший — ортонормалізувати перетворення об'єкта час від часу (можливо раз на кадр, якщо воно змінюється в кожному кадрі):
transform = transform.orthonormalized()
transform = transform.Orthonormalized();
Це зробить довжини всіх осей знову рівними 1.0 а кути між ними — рівними 90 градусів. Хоч в такому випадку масштабування об'єкта буде втрачено.
Краще не масштабувати вузли, які ви хочете обертати. Натомість, відмасштабуйте їх дочірні вузли (як-от MeshInstance). Якщо вам конче необхідно відмасштабувати вузол, то перезадайте масштаб після ортонормалізації:
transform = transform.orthonormalized()
transform = transform.scaled(scale)
transform = transform.Orthonormalized();
transform = transform.Scaled(scale);
Як отримати дані¶
Ви можете подумати: „Добре, а як мені отримати кути з матриці перетворення?. Якщо стисло — то ніяк. Вам потрібно перестати думати про кути.
Уявімо, вам потрібно вистрілити кулю в напрямку, куди дивиться ваш персонаж. Просто використайте його вісь уперед (зазвичай це Z або -Z).
bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED
bullet.Transform = transform;
bullet.LinearVelocity = transform.basis.z * BulletSpeed;
А чи дивиться ворог на гравця? Використайте скалярний добуток щоб дізнатись (про скалярний добуток можете почитати у статті Векторна математика):
# Get the direction vector from player to enemy
var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
enemy.im_watching_you(player)
// Get the direction vector from player to enemy
Vector3 direction = enemy.Transform.origin - player.Transform.origin;
if (direction.Dot(enemy.Transform.basis.z) > 0)
{
enemy.ImWatchingYou(player);
}
Зміщення вліво:
# Remember that +X is right
if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)
// Remember that +X is right
if (Input.IsActionPressed("strafe_left"))
{
TranslateObjectLocal(-Transform.basis.x);
}
Стрибок:
# Keep in mind Y is up-axis
if Input.is_action_just_pressed("jump"):
velocity.y = JUMP_SPEED
velocity = move_and_slide(velocity)
// Keep in mind Y is up-axis
if (Input.IsActionJustPressed("jump"))
velocity.y = JumpSpeed;
velocity = MoveAndSlide(velocity);
Загалом, усі дії з об'єктом можна здійснити використовуючи одні лише вектори.
Як задати дані¶
Звісно, є ситуації, коли вам необхідно задати параметри перетворення. Уявімо контролер від першої особи чи камеру, що обертається. Вони точно повинні використовувати кути, адже вам треба щоб перетворення відбувалось у певному порядку.
Тоді, тримайте кути окремо від матриці перетворення об'єкта та задавайте їх у кожному кадрі. Не намагайтесь зчитувати їх з об'єкта бо це неправильний спосіб використовувати перетворення.
Приклад, який дозволяє озиратись в стилі шутерів від першої особи:
# accumulators
var rot_x = 0
var rot_y = 0
func _input(event):
if event is InputEventMouseMotion and event.button_mask & 1:
# modify accumulated mouse rotation
rot_x += event.relative.x * LOOKAROUND_SPEED
rot_y += event.relative.y * LOOKAROUND_SPEED
transform.basis = Basis() # reset rotation
rotate_object_local(Vector3(0, 1, 0), rot_x) # first rotate in Y
rotate_object_local(Vector3(1, 0, 0), rot_y) # then rotate in X
// accumulators
private float _rotationX = 0f;
private float _rotationY = 0f;
public override void _Input(InputEvent @event)
{
if (@event is InputEventMouseMotion mouseMotion)
{
// modify accumulated mouse rotation
_rotationX += mouseMotion.Relative.x * LookAroundSpeed;
_rotationY += mouseMotion.Relative.y * LookAroundSpeed;
// reset rotation
Transform transform = Transform;
transform.basis = Basis.Identity;
Transform = transform;
RotateObjectLocal(Vector3.Up, _rotationX); // first rotate about Y
RotateObjectLocal(Vector3.Right, _rotationY); // then rotate about X
}
}
Як бачите, в таких випадках, простіше працювати з кутами, і застосовувати до перетворення лише їх кінцевий результат.
Інтерполяція з кватерніонами¶
Здійснити інтерполяцію між двома перетвореннями можна використавши кватерніони. Дізнатись, як працюють кватерніони можна деінде, в інтернеті. Зараз же, вам достатньо знати, що їх основна ціль — забезпечувати інтерполяцію найкоротшим шляхом. І якщо у вас є два обертання: кватерніон може плавно переходити від одного, до іншого, по найкоротшій з осей.
Кути обертання можна з легкістю перетворити в кватерніон.
# Convert basis to quaternion, keep in mind scale is lost
var a = Quat(transform.basis)
var b = Quat(transform2.basis)
# Interpolate using spherical-linear interpolation (SLERP).
var c = a.slerp(b,0.5) # find halfway point between a and b
# Apply back
transform.basis = Basis(c)
// Convert basis to quaternion, keep in mind scale is lost
var a = transform.basis.Quat();
var b = transform2.basis.Quat();
// Interpolate using spherical-linear interpolation (SLERP).
var c = a.Slerp(b, 0.5f); // find halfway point between a and b
// Apply back
transform.basis = new Basis(c);
Документація типу Quat має більше інформації про цей тип даних (він також може накопичувати перетворення, переміщувати точки тощо, хоч це й не так часто використовують). Пам'ятайте, якщо ви проінтерполюєте або застосуєте кватерніон до об'єкта багато разів, то його потрібно буде нормалізувати. Інакше, він почне втрачати точність.
Кватерніони корисні, якщо потрібно здійснити інтерполяцію камери, вздовж шляху, тощо. Вони дадуть правильний та гладенький результат.
Перетворення — це ваші найкращі друзі¶
Для більшості початківців, має пройти певний час, доки вони не звикнуть працювати з перетвореннями. Проте, щойно ви призвичаїтесь до них, ви оціните їх простоту та корисність.
Не соромтесь задавати питання на цю тему в `будь-якій інтернет-спільноті Godot<https://godotengine.org/community>`_ . І, коли ви наберетесь достатньо знань, будь ласка, допоможіть іншим!