Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Матриці та перетворення¶
Вступ¶
Перед тим як читати цю статтю, радимо вам пройти урок :ref:`doc_vector_math`так як вам потрібно знати базові концепції векторів щоб зрозуміти цю статтю.
Ця стаття розповідає про перетворення та про те, як ми представляємо їх у Godot за допомогою матриць. Це не є поглиблений посібник з матриць. Перетворення в основному застосовуються для переміщення, обертання та масштабування, тому ми зосередимося на тому, як це робити за допомогою матриць.
Більша частина цього посібника зосереджена на 2D і використовує Transform2D та Vector2, але перетворення в 3D працюють схожим чином.
Примітка
Як згадувалося в попередній статті, важливо пам'ятати, що в Godot, у 2D, вісь Y вказує вниз. На відміну від шкільного курсу лінійної алгебри, де вісь Y вказує вгору.
Примітка
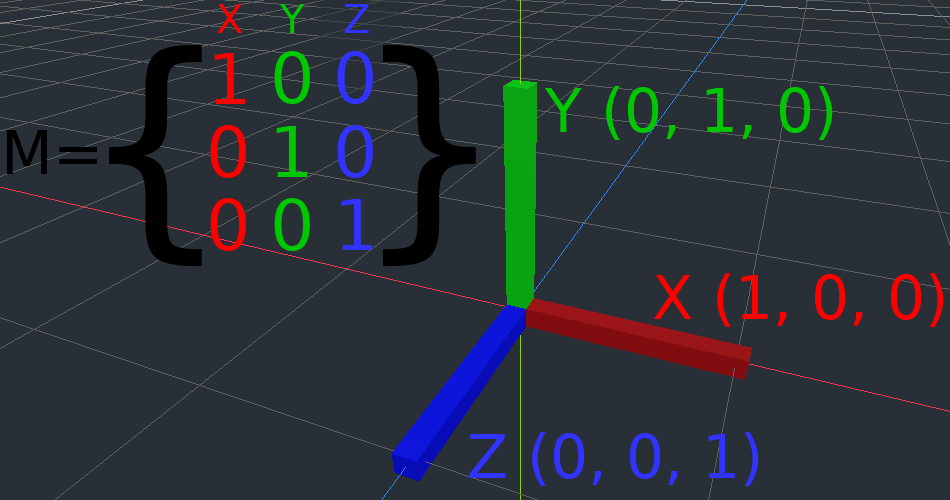
Умовність полягає в тому, що вісь X - червона, вісь Y - зелена, а вісь Z - синя. Ця стаття буде використовувати колір відповідно до цієї умовності, але синім кольором ми також будемо малювати вектор походження.
Компоненти матриці та Матриця Ідентичності¶
Матриця ідентичності - це перетворення без переміщення, обертання і масштабування. Почнемо з погляду на матрицю ідентичності і на те, як її компоненти пов'язані з тим, як вона візуально проявляється.
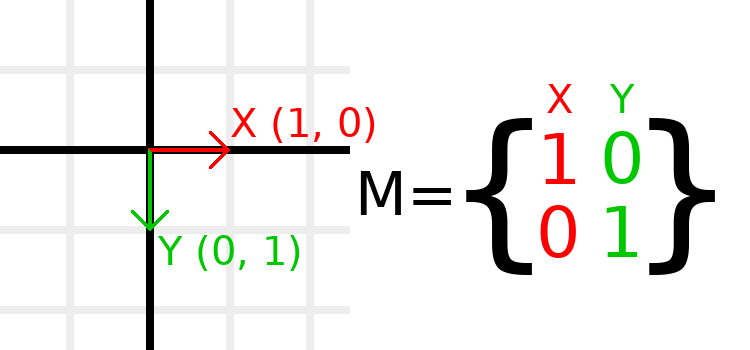
Матриці мають рядки та стовпці, а матриця перетворення має конкретні умовності щодо того, що робить кожен з них.
На зображенні вище ми бачимо, що червоний вектор X представлений першим стовпцем матриці, а зелений вектор Y - представлений другим стовпцем. Зміна стовпців змінить ці вектори. Ми побачимо, як ними можна маніпулювати в наступних прикладах.
Вам не варто чіплятися за безпосереднє маніпулювання рядками, бо зазвичай ми працюємо зі стовпцями. Однак ви можете думати про рядки матриці, як про вектори, які сприяють руху в заданому напрямку.
When we refer to a value such as t.x.y, that's the Y component of
the X column vector. In other words, the bottom-left of the matrix.
Similarly, t.x.x is top-left, t.y.x is top-right, and t.y.y
is bottom-right, where t is the Transform2D.
Масштабування за допомогою матриці перетворення¶
Масштабування є однією з найпростіших для розуміння операцій. Почнемо з розміщення логотипу Godot під нашими векторами, щоб ми могли візуально бачити вплив на об'єкт:
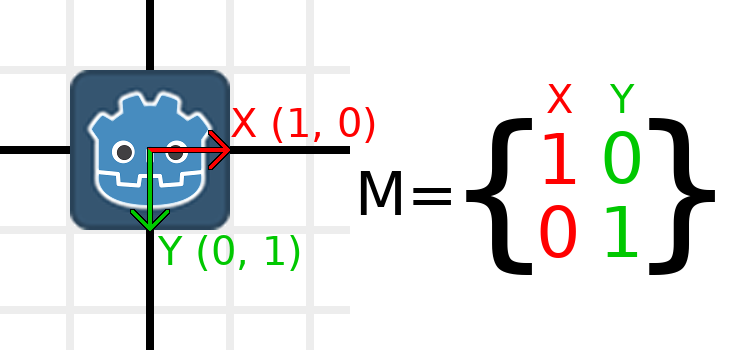
Тепер, щоб масштабувати матрицю, все, що нам потрібно зробити, це помножити кожен компонент на потрібний масштаб. Давайте збільшимо його на 2. 1 помножити на 2 стає 2, а 0 помножити на 2 стає 0, тому ми в кінцевому підсумку отримуємо це:
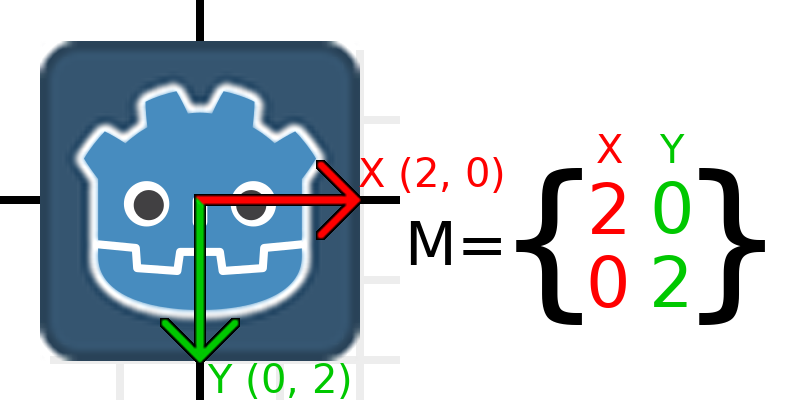
To do this in code, we multiply each of the vectors:
var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Scale
t.X *= 2;
t.Y *= 2;
Transform = t; // Change the node's transform to what we calculated.
Якби ми хотіли повернути його до початкового масштабу, ми могли б помножити кожен компонент на 0,5. Це майже все, що треба знати для масштабування матриці перетворення.
To calculate the object's scale from an existing transformation
matrix, you can use length() on each of the column vectors.
Примітка
In actual projects, you can use the scaled()
method to perform scaling.
Обертання за допомогою матриці перетворення¶
Почнемо з того самого логотипу Godot під матрицею ідентичності:

Припустимо, що ми хочемо повернути наш логотип за годинниковою стрілкою на 90 градусів. Зараз вісь X вказує праворуч, а вісь Y - вниз. Якщо ми уявімо їх поворот, то зрозуміємо, що нова вісь X повинна вказувати вниз, а нова вісь Y повинна вказувати ліворуч.
Ви можете уявити собі, що ви хапаєте, і логотип Godot, і його вектори, а потім крутите його відносно центру. Де б ви не спинили обертатися, орієнтація векторів визначає матрицю.
We need to represent "down" and "left" in normal coordinates,
so means we'll set X to (0, 1) and Y to (-1, 0). These are
also the values of Vector2.DOWN and Vector2.LEFT.
When we do this, we get the desired result of rotating the object:
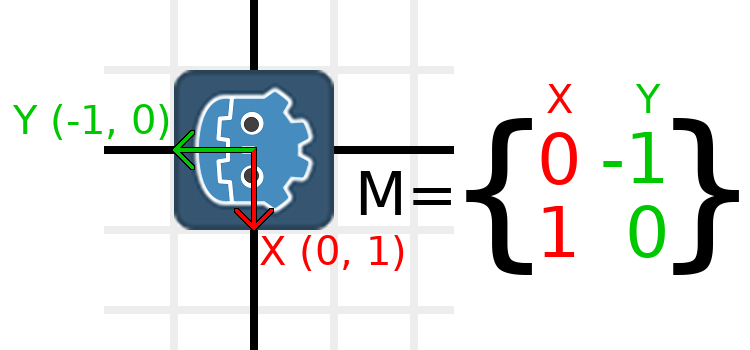
Якщо у вас виникли проблеми з розумінням вищесказаного, спробуйте таку вправу: Витніть з паперу квадрат, намалюйте на ньому вектори X і Y, помістіть його на розграфлений папір, потім поверніть його і занотуйте куди вказують вектори. (Примітка перекладача: Напрям вверх має координати (0, -1), вправо - (1, 0), вниз - (0, 1), вліво - (-1, 0), при обертанні картинки її вектори змінюють напрямок у який вказують).
Для виконання обертання в коді нам потрібно вміти обчислювати значення програмно. Це зображення показує формули, необхідні для обчислення матриці кута повороту. Не хвилюйтеся, якщо ця частина здається складною, я обіцяю, що це найважче, що вам потрібно знати.
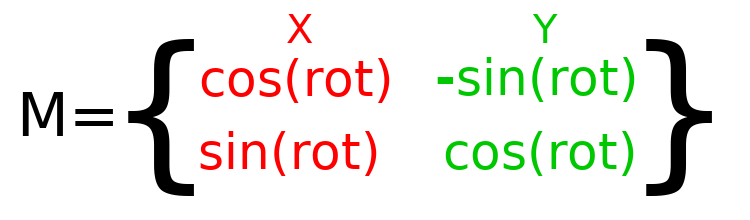
Примітка
Godot представляє всі обертання в радіанах, а не градусах. Повний поворот рівний TAU, або PI*2, радіан, а чверть повороту, на 90 градусів, - TAU/4, або PI/2 радіан. Використання TAU зазвичай дає більш читабельний код.
Примітка
Цікавий факт: На додаток до того, що Y в Godot вказує вниз, обертання представлене за годинниковою стрілкою. Це означає, що всі математичні та тригерні функції поводяться так само, як і система CCW Y-зверху, оскільки ці відмінності "скасовуються". Ви можете думати, що обертання в обох системах є "від X до Y".
In order to perform a rotation of 0.5 radians (about 28.65 degrees), we plug in a value of 0.5 to the formula above and evaluate to find what the actual values should be:
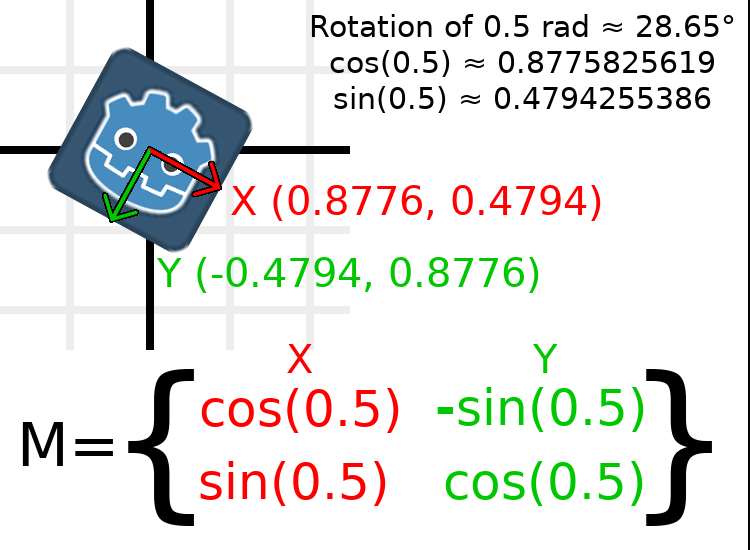
Ось як це буде зроблено в коді (помістіть скрипт на вузол Node2D):
var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we calculated.
float rot = 0.5f; // The rotation to apply.
Transform2D t = Transform2D.Identity;
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
Transform = t; // Change the node's transform to what we calculated.
To calculate the object's rotation from an existing transformation
matrix, you can use atan2(t.x.y, t.x.x), where t is the Transform2D.
Примітка
In actual projects, you can use the rotated()
method to perform rotations.
Основа матриці перетворення¶
So far we have only been working with the x and y, vectors, which
are in charge of representing rotation, scale, and/or shearing
(advanced, covered at the end). The X and Y vectors are together
called the basis of the transformation matrix. The terms "basis"
and "basis vectors" are important to know.
You might have noticed that Transform2D actually
has three Vector2 values: x, y, and origin.
The origin value is not part of the basis, but it is part of the
transform, and we need it to represent position. From now on we'll
keep track of the origin vector in all examples. You can think of
origin as another column, but it's often better to think of it as
completely separate.
Note that in 3D, Godot has a separate Basis structure for holding the three Vector3 values of the basis, since the code can get complex and it makes sense to separate it from Transform3D (which is composed of one Basis and one extra Vector3 for the origin).
Переміщення за допомогою матриці перетворення¶
Changing the origin vector is called translating the transformation
matrix. Translating is basically a technical term for "moving" the
object, but it explicitly does not involve any rotation.
Давайте розглянемо приклад, щоб зрозуміти це. Ми почнемо з матриці ідентичності, як минулого разу, за винятком того, що цього разу ми будемо відстежувати вектор походження.
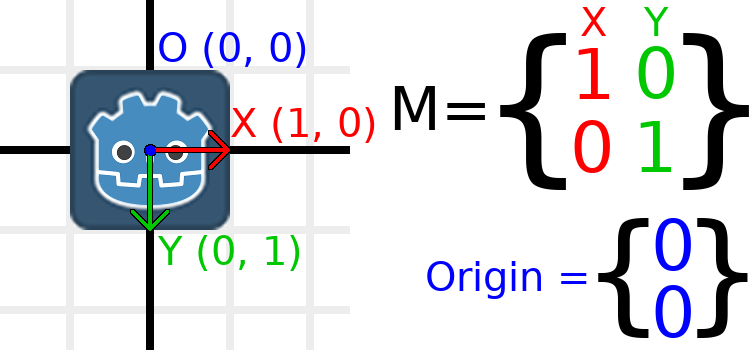
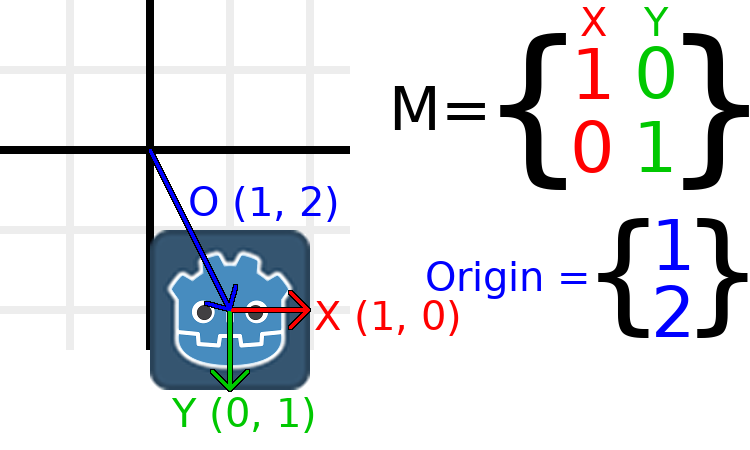
If we want to move the object to a position of (1, 2), we need
to set its origin vector to (1, 2):
There is also a translated() method, which performs a different
operation to adding or changing origin directly. The translated()
method will translate the object relative to its own rotation.
For example, an object rotated 90 degrees clockwise will move to
the right when translated() with Vector2.UP.
Примітка
Godot в 2D використовує координати, засновані на пікселях, тому в реальних проектах ви будете переміщувати на сотні одиниць.
Збираємо все це докупи¶
We're going to apply everything we mentioned so far onto one transform. To follow along, create a project with a Sprite2D node and use the Godot logo for the texture resource.
Давайте встановимо переміщення на (350, 150), поворот на -0,5 радіан і масштаб на 3. Я опублікував скріншот, і код, для його відтворення, але закликаю вас спробувати відтворити скріншот, не заглядаючи в код!
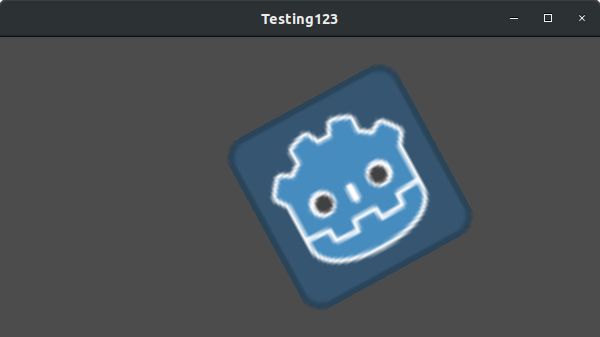
var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Translation
t.Origin = new Vector2(350, 150);
// Rotation
float rot = -0.5f; // The rotation to apply.
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
// Scale
t.X *= 3;
t.Y *= 3;
Transform = t; // Change the node's transform to what we calculated.
Перекоси за допомогою матриці перетворення (додатково)¶
Примітка
Якщо ви шукаєте інформацію тільки про використання матриць перетворення, не соромтеся пропустити цей розділ статті. Цей розділ досліджує мало коли використовуваний аспект матриць перетворення з метою формування розуміння їх.
Node2D provides a shearing property out of the box.
Можливо, ви помітили, що перетворення має більше ступенів свободи, ніж поєднання вищезазначених дій. Основа матриці 2D-перетворення має чотири загальних числа у двох значеннях Vector2, тоді як значення обертання та Вектор2 для масштабу мають лише 3 числа. Концепція високого рівня з обмеження ступенів свободи дозволяє перекоси.
Як правило, базові вектори у вас завжди будуть перпендикулярні один одному. Однак перекоси можуть бути корисними в деяких ситуаціях, а їх розуміння допомагає зрозуміти, як працюють перетворення.
Щоб візуально показати вам, як це буде виглядати, давайте накладемо сітку на логотип Godot:
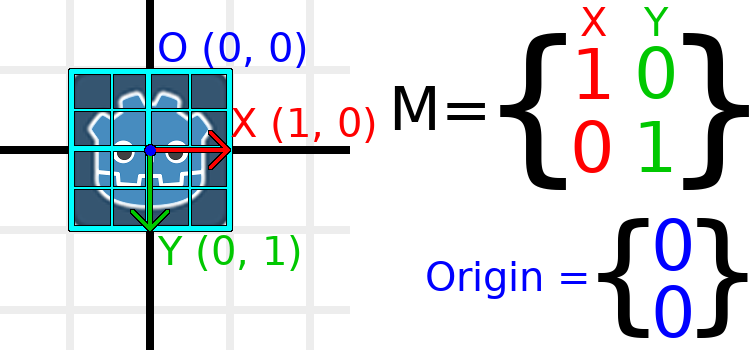
Кожна точка на цій сітці є отримана за допомогою додавання основних векторів. Нижній правий кут рівний X + Y, а верхній правий кут рівний X - Y. Якщо ми змінимо вектори основи, то з ними зрушиться вся сітка, так як сітка складається з основних векторів. Всі лінії на сітці, які в даний час паралельні, залишаться паралельними, незалежно від того, які зміни ми вносимо в основні вектори.
Як приклад, давайте встановимо Y на (1, 1):
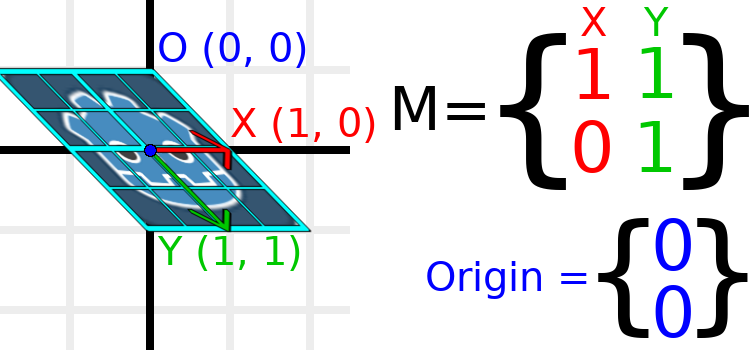
var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Shear by setting Y to (1, 1)
t.Y = Vector2.One;
Transform = t; // Change the node's transform to what we calculated.
Примітка
Ви не можете встановити необроблені значення Transform2D у редакторі, тому ви повинні використовувати код, якщо хочете перекосити об'єкт.
Через те, що вектори більше не перпендикулярні, об'єкт перекосився. Нижній центр сітки, який (0, 1) відносно себе, у світовому положенні тепер розташований (1, 1).
Внутрішні координати об'єкта називаються текстурними координатами, тому давайте запозичимо цю термінологію сюди. Щоб знайти світову позицію з відносної позиції використовується формула - U * X + V * Y, де U і V - числа, а X і Y - базові вектори.
Нижній правий кут сітки, який в текстурних координатах завжди знаходиться на (1, 1), світових знаходиться на (2, 1), які розраховуються від X*1 + Y*1, що дорівнює (1, 0) + (1, 1), або (1 + 1, 0 + 1), або (2, 1). Це узгоджується з нашим спостереженням за тим, де знаходиться правий нижній кут зображення.
Аналогічно, верхній правий кут сітки, який в текстурних координатах завжди знаходиться на (1, -1), у світових знаходиться на (0, -1), які вираховуються з X*1 + Y*-1, що дорівнює (1, 0) - (1, 1), або (1 - 1, 0 - 1), або (0, -1). Це узгоджується з нашим спостереженням за тим, де знаходиться верхній правий кут зображення.
Сподіваюся, тепер ви повністю розумієте, як матриця перетворення впливає на об'єкт, і взаємозв'язок між основними векторами і тим, як "внутрішні координати" об'єкта змінюють своє світове положення.
Примітка
У Godot вся математика перетворення виконується відносно батьківського вузла. Коли ми маємо на увазі "світову позицію", то говоримо про позицію відносно батьківського вузла, якщо у вузла є батько.
Якщо ви хочете отримати додаткові пояснення, вам слід переглянути чудове відео 3Blue1Brown про лінійні перетворення: https://www.youtube.com/watch?v=kYB8IZa5AuE
Практичне застосування перетворень¶
In actual projects, you will usually be working with transforms inside transforms by having multiple Node2D or Node3D nodes parented to each other.
However, it's useful to understand how to manually calculate the values we need. We will go over how you could use Transform2D or Transform3D to manually calculate transforms of nodes.
Конвертування позицій між перетвореннями¶
Є багато випадків, коли вам треба конвертувати позицію в і зовні перетворення. Наприклад, якщо у вас є позиція відносно гравця і ви хотіли б знайти світову (відносну батька) позицію, або якщо у вас є світова позиція і ви хочете знати, де вона знаходиться відносно гравця.
We can find what a vector relative to the player would be defined in
world space as using the * operator:
# World space vector 100 units below the player.
print(transform * Vector2(0, 100))
// World space vector 100 units below the player.
GD.Print(Transform * new Vector2(0, 100));
And we can use the * operator in the opposite order to find a what world
space position would be if it was defined relative to the player:
# Where is (0, 100) relative to the player?
print(Vector2(0, 100) * transform)
// Where is (0, 100) relative to the player?
GD.Print(new Vector2(0, 100) * Transform);
Примітка
Якщо ви заздалегідь знаєте, що вузол перетворення розташований на (0, 0), то можете використовувати методи basis_xform, або basis_xform_inv, які пропускають конвертацію.
Переміщення об'єкта відносно себе¶
Поширеною операцією, особливо в 3D-іграх, є переміщення об'єкта відносно себе. Наприклад, у шутерах від першої особи потрібно, щоб персонаж рухався вперед (вісь -Z) під час натискання клавіші W.
Since the basis vectors are the orientation relative to the parent, and the origin vector is the position relative to the parent, we can add multiples of the basis vectors to move an object relative to itself.
Цей код переміщує об'єкт на 100 одиниць праворуч:
transform.origin += transform.x * 100
Transform2D t = Transform;
t.Origin += t.X * 100;
Transform = t;
Для переміщення в 3D вам потрібно буде замінити x на basis.x.
Примітка
In actual projects, you can use translate_object_local in 3D
or move_local_x and move_local_y in 2D to do this.
Застосування перетворень на перетвореннях¶
Одна з найважливіших речей, які потрібно знати про перетворення, - це те, що ви можете використовувати кілька їх разом. Перетворення батьківського вузла впливає на всіх його дітей. Давайте розглянемо приклад.
На цьому зображенні дочірній вузол має приставку "2" до назв компонентів, щоб відрізнити їх від компонентів батьківського вузла. Це може виглядати трохи приголомшливо з такою кількістю чисел, але пам'ятайте, що кожне число відображається двічі (поруч зі стрілками, а також у матрицях), і що майже половина чисел дорівнює нулю.
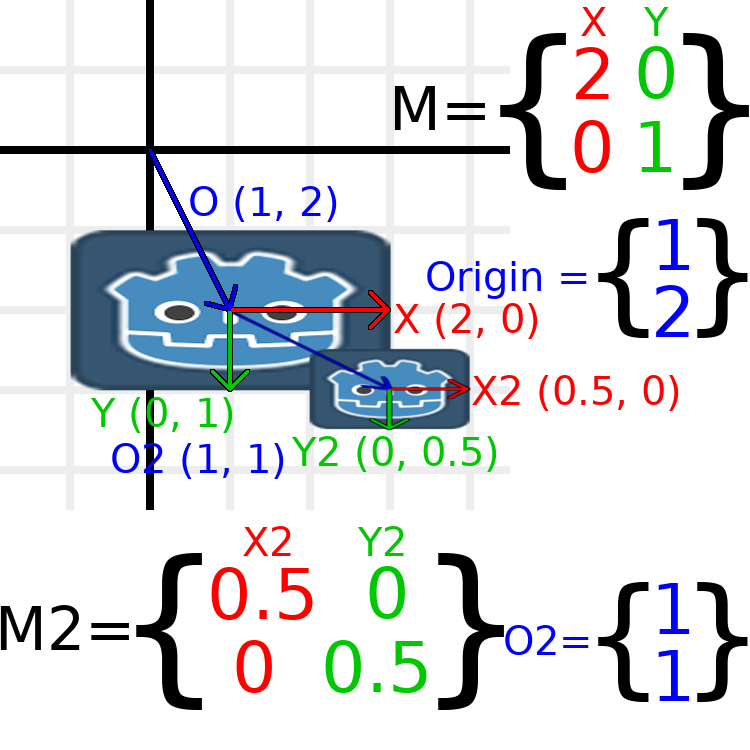
Єдині перетворення, що відбуваються тут, - це те, що батьківському вузлу була наданий масштаб (2, 1), дитині - масштаб (0,5, 0,5), і обом вузлам були надані позиції.
All child transformations are affected by the parent transformations.
The child has a scale of (0.5, 0.5), so you would expect it to be
a 1:1 ratio square, and it is, but only relative to the parent.
The child's X vector ends up being (1, 0) in world space, because
it is scaled by the parent's basis vectors.
Similarly, the child node's origin vector is set to (1, 1), but this
actually moves it (2, 1) in world space, due to the parent node's
basis vectors.
Щоб розрахувати перетворення дитини відносно світового простору вручну, ми можемо використовувати такий код:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y
# Change the node's transform to what we calculated.
transform = Transform2D(basis_x, basis_y, origin)
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Calculate the child's world space transform
// origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
Vector2 origin = parent.X * child.Origin.X + parent.Y * child.Origin.Y + parent.Origin;
// basisX = (2, 0) * 0.5 + (0, 1) * 0 = (0.5, 0)
Vector2 basisX = parent.X * child.X.X + parent.Y * child.X.Y;
// basisY = (2, 0) * 0 + (0, 1) * 0.5 = (0.5, 0)
Vector2 basisY = parent.X * child.Y.X + parent.Y * child.Y.Y;
// Change the node's transform to what we calculated.
Transform = new Transform2D(basisX, basisY, origin);
In actual projects, we can find the world transform of the child by
applying one transform onto another using the * operator:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Change the node's transform to what would be the child's world transform.
transform = parent * child
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Change the node's transform to what would be the child's world transform.
Transform = parent * child;
Примітка
При множенні матриць, порядок має значення! Не змішуйте їх.
Нарешті, застосування перетворення ідентичності завжди нічого не зробить.
Якщо ви хочете отримати додаткове пояснення, вам слід переглянути чудове відео 3Blue1Brown про матричну композицію: https://www.youtube.com/watch?v=XkY2DOUCWMU
Інвертування матриці перетворення¶
The "affine_inverse" function returns a transform that "undoes" the previous transform. This can be useful in some situations. Let's take a look at a few examples.
Множення інвертованого перетворення на нормальне перетворення скасовує всі перетворення:
var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.
Transform2D ti = Transform.AffineInverse();
Transform2D t = ti * Transform;
// The transform is the identity transform.
Transforming a position by a transform and its inverse results in the same position:
var ti = transform.affine_inverse()
position = transform * position
position = ti * position
# The position is the same as before.
Transform2D ti = Transform.AffineInverse();
Position = Transform * Position;
Position = ti * Position;
// The position is the same as before.
Як усе це працює в 3D?¶
One of the great things about transformation matrices is that they work very similarly between 2D and 3D transformations. All the code and formulas used above for 2D work the same in 3D, with 3 exceptions: the addition of a third axis, that each axis is of type Vector3, and also that Godot stores the Basis separately from the Transform3D, since the math can get complex and it makes sense to separate it.
Всі концепції того, як працюють переміщення, обертання, масштабування і скошення в 3D, такі самі, як і в 2D. Для масштабування беремо кожен компонент і множимо його; щоб повернути, ми змінюємо, напрям кожного основного вектора; для переміщення ми маніпулюємо походженням;а для перекосів, ми змінюємо основні вектори, щоб вони були неперпендикулярними.
Якщо хочете, можете по-експериментувати з перетвореннями, щоб зрозуміти їх роботу. Godot дозволяє редагувати матриці 3D-перетворення безпосередньо в Інспекторі. Ви можете завантажити цей проект, який має кольорові лінії та кубики, щоб допомогти візуалізувати вектори Basis та походження як у 2D, так і в 3D: https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform
Примітка
You cannot edit Node2D's transform matrix directly in Godot 4.0's inspector. This may be changed in a future release of Godot.
Якщо хочете отримати додаткове пояснення, вам слід ознайомитися з чудовим відео 3Blue1Brown про 3D-лінійні перетворення: https://www.youtube.com/watch?v=rHLEWRxRGiM
Представлення обертання в 3D (додатково)¶
Найбільша відмінність між матрицями перетворення 2D і 3D полягає в тому, як ви представляєте обертання саме по собі без базових векторів.
With 2D, we have an easy way (atan2) to switch between a transformation matrix and an angle. In 3D, rotation is too complex to represent as one number. There is something called Euler angles, which can represent rotations as a set of 3 numbers, however, they are limited and not very useful, except for trivial cases.
In 3D we do not typically use angles, we either use a transformation basis (used pretty much everywhere in Godot), or we use quaternions. Godot can represent quaternions using the Quaternion struct. My suggestion to you is to completely ignore how they work under-the-hood, because they are very complicated and unintuitive.
Однак, якщо вам дійсно треба знати, як це працює, ось деякі великі ресурси, з якими ви можете ознайомитися:
https://www.youtube.com/watch?v=mvmuCPvRoWQ