Поглиблена векторна алгебра¶

Площини¶

Скалярний добуток має одну цікаву властивість, пов'язану з одиничними векторами. Уявіть, нескінченну площину, перпендикулярну до цього вектора, яка проходить крізь початок координат . Площина ділить простір на верхній(над площиною) та нижній (під площиною) півпростори. І, напротивагу тому, що думає більшість людей, їх можна використовувати в 2D геометрії:

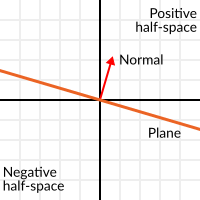
Перпендикулярні до поверхні одиничні вектори (які описують орієнтацію поверхні) називаються одиничними нормальними векторами. Але частіше їх називають просто нормалями. Нормалі мають площини, вони використовуються в 3D геометрії (щоби визначати куди дивиться кожна грань чи вершина), тощо. Нормаль — це одиничний вектор, який так називається через своє використання (так само як точка (0,0) називається початком координат просто тому, що ми вирішили відраховувати координати з цієї точки!).

Все настільки ж просто як здається. площина проходить крізь нульову точку а її поверхня перпендикулярна до одиничного вектора (або нормалі). Сторона, яка дивиться в той же бік, що й нормаль відділяє верхній півпростір, а інша — нижній півпростір. В 3D все так само, але площина — це тепер нескінченна поверхня (уявіть безконечний лист паперу, який можна крутити навколо нульової точки) замість лінії.

Відстань до площини¶

Тепер, коли вам ясно, що таке площина, повернімось до скалярного добутку. Результат скалярного добутку між одиничним вектором та будь-якою точкою в просторі (так, цього разу ми множимо вектор на положення) являється відстанню від точки до площини:

var distance = normal.dot(point)

var distance = normal.Dot(point);

При чому не просто відстанню. Якщо точка знаходиться в нижньому півпросторі, то відстань буде від'ємною:

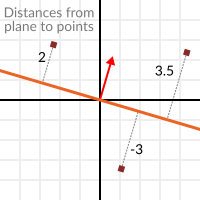
Так ми можемо дізнатись, з якого боку площини знаходиться точка.

Подалі від центру¶

Знаю, ви зараз думаєте: „Це все цікаво, але справжні площини розкидані по всьому просторі, а не лише на початку координат!“. Ви хочете справжніх площин і ви хочете їх зараз.

Пам'ятайте, що площини не лише розділяють простір надвоє, а й мають полярність. Може статись так, що дві площини ідеально збігаються одна з одною, але вони дивляться у протилежні боки, а їх верхні та нижні напівпростори поміняні місцями.

Враховуючи це, опишімо площину, через нормаль N та відстань до початку координат D, яка є числом. Таким чином площину можна описати як N і D. Наприклад:

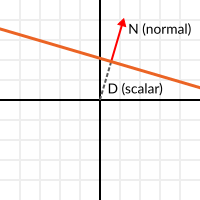
Для 3D, Godot має вбудований тип :ref:`Plane <class_Plane>`який цим займається.

N і D можуть описати будь-яку площину в просторі, як в 2D, так і в 3D (залежно від розмірності вектора N) і всі формули також працюють у різних вимірах. Завжди, D — це відстань від початку координат до площини в напрямку N. Наприклад, якщо ви хочете досягти хоч якоїсь точки на площині, то просто обрахуйте:

var point_in_plane = N*D

var pointInPlane = N * D;

Так ми розтягнемо (або скоротимо) вектор нормалі, щоби він торкався площини. Спершу може бути незрозуміло, але все простіше, ніж здається. Якщо ми хочемо знайти відстань від точки до площини, ми робимо все те ж саме, а потім вираховуємо відстань:

var distance = N.dot(point) - D

var distance = N.Dot(point) - D;

Те ж саме, але з використанням вбудованої функції:

var distance = plane.distance_to(point)

var distance = plane.DistanceTo(point);

Ця відстань також може бути як додатною, так і від'ємною.

Щоб перевернути площину потрібно замінити N та D на протилежні відповідники. Результатом цих дій буде площина, яка знаходитиметься на тому ж місці, але вивернутими напівпросторами:

N = -N
D = -D

N = -N;
D = -D;

Звісно, Godot має операцію для цього у класі :ref:`Plane <class_Plane>, тому код:

var inverted_plane = -plane

var invertedPlane = -plane;

Буде працювати так, як ви очікуєте.

Запам'ятайте, головна користь від площини: ви можете визначити відстань до неї. Що ж в цьому такого корисного? Багато чого! Розгляньмо декілька прикладів...

Побудова площини в 2D¶

Площини не беруться нізвідки, їх потрібно створювати. Створювати їх в 2D дуже просто. Для цього потрібен вектор з точкою або дві точки у просторі.

У першому випадку, більша частина роботи вже зроблена, так як нормаль вже обчислена. Тому просто обчисліть D взявши скалярний добуток нормалі та точки.

var N = normal
var D = normal.dot(point)

var N = normal;
var D = normal.Dot(point);

Натомість, для двох точок, існує дві площини, які проходять крізь них, але розвернуті в протилежні боки. Щоб обчислити нормаль з двох точок, спершу потрібно знайти вектор напрямку між ними, а потім повернути його на 90° в одну зі сторін:

# Calculate vector from `a` to `b`.
var dvec = (point_b - point_a).normalized()
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)

// Calculate vector from `a` to `b`.
var dvec = (pointB - pointA).Normalized();
// Rotate 90 degrees.
var normal = new Vector2(dvec.y, -dvec.x);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.y, dvec.x);

Далі все аналогічно попередньому прикладу, обидві точки point_a, або point_b підходять, так як вони лежать на одній площині:

var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)

var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);

Зробити це ж саме в 3D трохи складніше, нижче описано, як саме.

Приклади площин¶

Ось простий приклад ситуації, де в нагоді стануть площини. Уявіть, що у вас є опуклий багатокутник: прямокутник, трапеція, трикутник чи будь-який інший багатокутник в якого немає увігнутих сторін.

Для кожної сторони багатокутника, побудуймо пряму, яка проходить крізь цю сторону. Коли ми матимемо список всіх таких площин, ми зможемо робити багато цікавих речей, наприклад: перевіряти чи знаходиться точка всередині багатокутника.

Якщо пройшовшись по всім площинам ми знайдемо площину, для якої відстань від цікавої нам точки до неї додатна, то це означатиме, що ця точка знаходиться за межами багатокутника. Якщо ж таких площин немає, то точка знаходиться всередині.

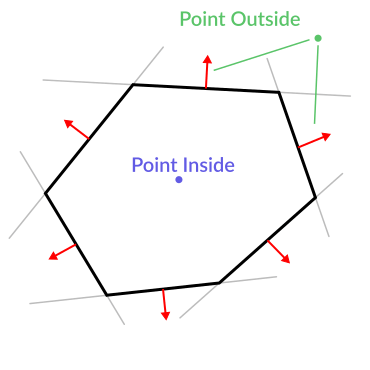
У коді, це виглядає приблизно ось так:

var inside = true
for p in planes:
    # check if distance to plane is positive
    if (p.distance_to(point) > 0):
        inside = false
        break # with one that fails, it's enough

var inside = true;
foreach (var p in planes)
{
    // check if distance to plane is positive
    if (p.DistanceTo(point) > 0)
    {
        inside = false;
        break; // with one that fails, it's enough
    }
}

Круто, а? Але все може бути навіть краще! Доклавши трохи більше зусиль ми можемо дізнатись чи перетинаються між собою два опуклих багатокутники. Спосіб зробити це називається „теорема про розділову гіперплощину“. Її використовують більшість інженерів та фізиків для визначення зіткнень об'єктів.

Якщо для визначення того, чи знаходиться точка ззовні від багатокутника, достатньо знайти сторону яка має додатну відстань до неї; то для другого багатокутника, потрібно знайти в першому таку сторону, для якої всі вершини другого багатокутника мають додатну відстань до неї. Спершу ми перевіряємо всі сторони прямокутника A та точки прямокутника B, потім — всі сторони B й точки A:

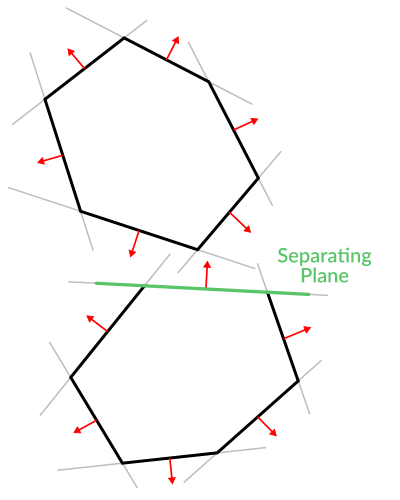
У коді, це виглядає приблизно ось так:

var overlapping = true

for p in planes_of_A:
    var all_out = true
    for v in points_of_B:
        if (p.distance_to(v) < 0):
            all_out = false
            break

    if (all_out):
        # a separating plane was found
        # do not continue testing
        overlapping = false
        break

if (overlapping):
    # only do this check if no separating plane
    # was found in planes of A
    for p in planes_of_B:
        var all_out = true
        for v in points_of_A:
            if (p.distance_to(v) < 0):
                all_out = false
                break

        if (all_out):
            overlapping = false
            break

if (overlapping):
    print("Polygons Collided!")

var overlapping = true;

foreach (Plane plane in planesOfA)
{
    var allOut = true;
    foreach (Vector3 point in pointsOfB)
    {
        if (plane.DistanceTo(point) < 0)
        {
            allOut = false;
            break;
        }
    }

    if (allOut)
    {
        // a separating plane was found
        // do not continue testing
        overlapping = false;
        break;
    }
}

if (overlapping)
{
    // only do this check if no separating plane
    // was found in planes of A
    foreach (Plane plane in planesOfB)
    {
        var allOut = true;
        foreach (Vector3 point in pointsOfA)
        {
            if (plane.DistanceTo(point) < 0)
            {
                allOut = false;
                break;
            }
        }

        if (allOut)
        {
            overlapping = false;
            break;
        }
    }
}

if (overlapping)
{
    GD.Print("Polygons Collided!");
}

Як можете побачити, площини дуже корисні. І це лише вершина айсберга. Можливо вас цікавлять увігнуті многокутники. Зазвичай їх розділяють на декілька опуклих многокутників або використовують техніку що називається БРП (яку більше майже не використовують).

Визначення зіткнень в 3D¶

За те, що ви були терплячими та витримали цей довжелезний урок, ось вам ще одна мудрість. Можливо вона вам не знадобиться (Godot і сам прекрасно визначає зіткнення об'єктів) але вона корисна для розуміння більшости фізичних рушіїв та бібліотек:)

Пам'ятаєте, як для визначення перетину опуклих многокутників в 2D ми розглядали їх як набір двовимірних площин(прямих)? Ви могли визначити чи точка була всередині опуклої фігури або чи дві двовимірні фігури перетинаються.

Цей підхід працює і в 3D. Якщо два 3D багатогранника перетинаються, вам не вдасться знайти розділову площину. Якщо ж така площина знайдена, то фігури напевно не перетинаються.

Нагадуємо, що площина розділова, якщо всі точки багатокутника A знаходяться з одного боку площини, а всі точки B — з іншого. Ця площина завжди лежить на одній зі сторін одного з багатокутників A чи B.

В 3D ж, існує проблема з цим підходом, бо іноді трапляється, що знайти розділову площину неможливо. Наприклад в такій ситуації:

Щоб уникнути такого, потрібно перевірити ще декілька площин. Ці площини — векторний добуток ребер многогранника A і векторний добуток ребер многогранника B

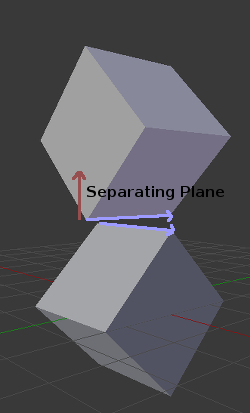
Кінцевий алгоритм виглядає десь так:

var overlapping = true

for p in planes_of_A:
    var all_out = true
    for v in points_of_B:
        if (p.distance_to(v) < 0):
            all_out = false
            break

    if (all_out):
        # a separating plane was found
        # do not continue testing
        overlapping = false
        break

if (overlapping):
    # only do this check if no separating plane
    # was found in planes of A
    for p in planes_of_B:
        var all_out = true
        for v in points_of_A:
            if (p.distance_to(v) < 0):
                all_out = false
                break

        if (all_out):
            overlapping = false
            break

if (overlapping):
    for ea in edges_of_A:
        for eb in edges_of_B:
            var n = ea.cross(eb)
            if (n.length() == 0):
                continue

            var max_A = -1e20 # tiny number
            var min_A = 1e20 # huge number

            # we are using the dot product directly
            # so we can map a maximum and minimum range
            # for each polygon, then check if they
            # overlap.

            for v in points_of_A:
                var d = n.dot(v)
                max_A = max(max_A, d)
                min_A = min(min_A, d)

            var max_B = -1e20 # tiny number
            var min_B = 1e20 # huge number

            for v in points_of_B:
                var d = n.dot(v)
                max_B = max(max_B, d)
                min_B = min(min_B, d)

            if (min_A > max_B or min_B > max_A):
                # not overlapping!
                overlapping = false
                break

        if (not overlapping):
            break

if (overlapping):
   print("Polygons collided!")

var overlapping = true;

foreach (Plane plane in planesOfA)
{
    var allOut = true;
    foreach (Vector3 point in pointsOfB)
    {
        if (plane.DistanceTo(point) < 0)
        {
            allOut = false;
            break;
        }
    }

    if (allOut)
    {
        // a separating plane was found
        // do not continue testing
        overlapping = false;
        break;
    }
}

if (overlapping)
{
    // only do this check if no separating plane
    // was found in planes of A
    foreach (Plane plane in planesOfB)
    {
        var allOut = true;
        foreach (Vector3 point in pointsOfA)
        {
            if (plane.DistanceTo(point) < 0)
            {
                allOut = false;
                break;
            }
        }

        if (allOut)
        {
            overlapping = false;
            break;
        }
    }
}

if (overlapping)
{
    foreach (Vector3 edgeA in edgesOfA)
    {
        foreach (Vector3 edgeB in edgesOfB)
        {
            var normal = edgeA.Cross(edgeB);
            if (normal.Length() == 0)
            {
                continue;
            }

            var maxA = float.MinValue; // tiny number
            var minA = float.MaxValue; // huge number

            // we are using the dot product directly
            // so we can map a maximum and minimum range
            // for each polygon, then check if they
            // overlap.

            foreach (Vector3 point in pointsOfA)
            {
                var distance = normal.Dot(point);
                maxA = Mathf.Max(maxA, distance);
                minA = Mathf.Min(minA, distance);
            }

            var maxB = float.MinValue; // tiny number
            var minB = float.MaxValue; // huge number

            foreach (Vector3 point in pointsOfB)
            {
                var distance = normal.Dot(point);
                maxB = Mathf.Max(maxB, distance);
                minB = Mathf.Min(minB, distance);
            }

            if (minA > maxB || minB > maxA)
            {
                // not overlapping!
                overlapping = false;
                break;
            }
        }

        if (!overlapping)
        {
            break;
        }

    }
}

if (overlapping)
{
    GD.Print("Polygons Collided!");
}

Додаткова інформація¶

Щоб дізнатись більше про використання векторної математики в Godot, почитайте цю статтю:

Матриці та перетворення

Якщо вам хотілося б кращого пояснення, погляньте на прекрасну серію відео "Essence of Linear Algebra" від 3Blue1Brown: https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab