Attention: Here be dragons

This is the latest (unstable) version of this documentation, which may document features not available in or compatible with released stable versions of Godot.

Checking the stable version of the documentation...

Vektorová matematika

Úvod

Tento tutoriál je krátký a praktický úvod do lineární algebry s uplatněním ve vývoji her. Lineární algebra se zabývá vektory a jejich využitím. Vektory mají mnoho uplatnění ve vývoji ve 2D i 3D a Godot je značně používá.

Poznámka

Tento tutoriál není oficiální učebnice lineární algebry. My se pouze podíváme na uplatnění pro vývoj her. Pro širší pohled na matematiku navštivte https://www.khanacademy.org/math/linear-algebra

Soustavy souřadnic (2D)

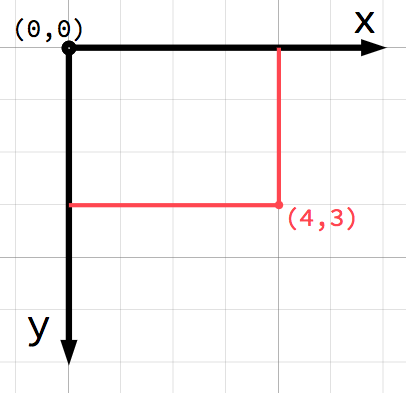
Ve 2D prostoru jsou souřadnice definovány pomocí vodorovné osy (x) svislé osy (y) . Konkrétní pozice ve 2D prostoru je zapsána jako dvojice hodnot , např. (4, 3).

Poznámka

Pokud začínáte s počítačovou grafikou, může se zdát zvláštní, že kladná část osy y směřuje dolů místo nahoru, jak jste se učili na hodině matematiky. Ve většině aplikací počítačové grafiky je to však běžné.

Libovolná pozice ve 2D rovině může být takto vyjádřena dvojicí čísel. Nicméně o pozici (4, 3) můžeme uvažovat jako o odklonu (offset) od bodu (0, 0) neboli počátku (origin). Nakreslíme šipku směřující od počátku k našemu bodu:

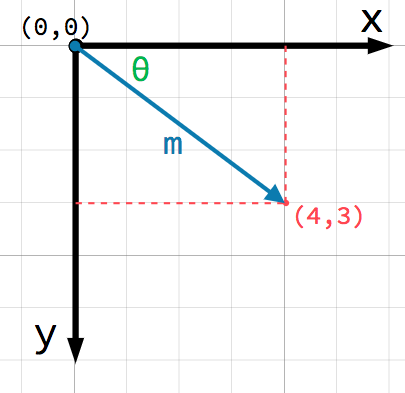
This is a vector. A vector represents a lot of useful information. As well as telling us that the point is at (4, 3), we can also think of it as an angle θ (theta) and a length (or magnitude) m. In this case, the arrow is a position vector - it denotes a position in space, relative to the origin.

Velmi důležitým bodem ke zvážení ohledně vektorů, je že představují pouze relativní směr a velikost. Neexistuje žádný koncept pozice vektoru. Následující dva vektory jsou totožné:

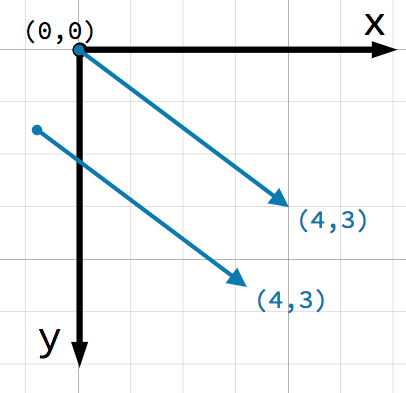
Oba vektory představují bod 4 jednotky vpravo a 3 jednotky pod nějakým počátečním bodem. Nezáleží na tom, kde v rovině vektor nakreslíte, vždy představuje relativní směr a velikost.

Operace s vektory

K odkazování na vektor můžete použít kteroukoli metodu (souřadnice x a y nebo úhel a velikost), ale programátoři obvykle používají pohodlnější souřadnicový zápis. Např. v Godot se počátek nachází v levém horním rohu obrazovky, takže pro umístění 2D uzlu pojmenovaného Node2D 400 pixelů vpravo a 300 pixelů dolů, použijeme následující kód:

$Node2D.position = Vector2(400, 300)

var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);

Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules discussed in this article apply to both types, and wherever we link to Vector2 methods in the class reference, you can also check out their Vector3 counterparts.

Přistupování k částem vektoru

K jednotlivým složkám vektoru lze přistupovat přímo podle jména.

# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1

// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;

Sčítání vektorů

Při sčítání nebo odečítání dvou vektorů se sčítají odpovídající složky:

var c = a + b  # (2, 5) + (3, 1) = (5, 6)

var c = a + b;  // (2, 5) + (3, 1) = (5, 6)

To můžeme znázornit také graficky přičtením druhého vektoru na konec prvního:

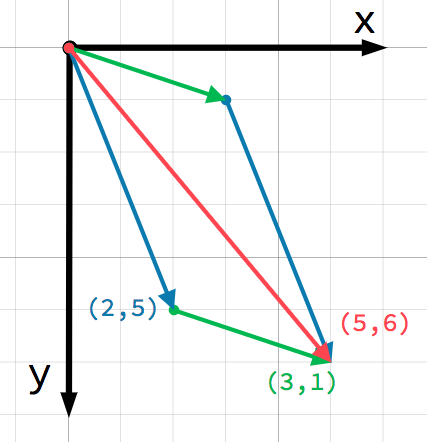
Všimněte si, že součet a + b dává stejný výsledek jako b + a.

Násobení skalárem

Poznámka

Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.

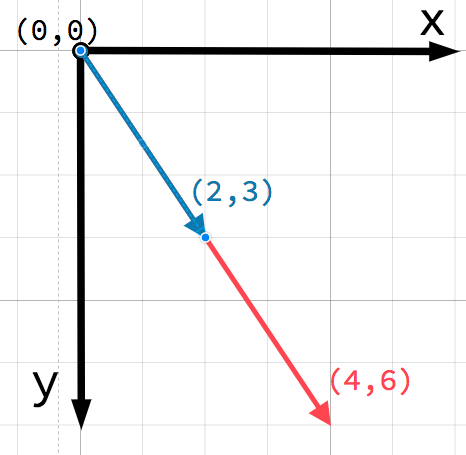
Vektor může být násoben skalárem:

var c = a * 2  # (2, 5) * 2 = (4, 10)
var d = b / 3  # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)

var c = a * 2;  // (2, 5) * 2 = (4, 10)
var d = b / 3;  // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)

Poznámka

Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.

Praktické aplikace

Podívejme se na dvě běžná použití sčítání a odčítání vektorů.

Pohyb

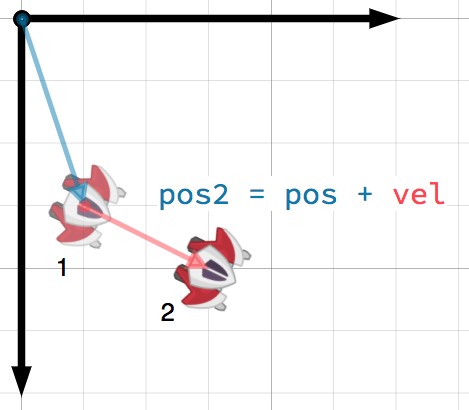
A vector can represent any quantity with a magnitude and direction. Typical examples are: position, velocity, acceleration, and force. In this image, the spaceship at step 1 has a position vector of (1, 3) and a velocity vector of (2, 1). The velocity vector represents how far the ship moves each step. We can find the position for step 2 by adding the velocity to the current position.

Tip

Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.

In a typical 2D game scenario, you would have a velocity in pixels per second, and multiply it by the delta parameter (time elapsed since the previous frame) from the _process() or _physics_process() callbacks.

Směřování k cíli

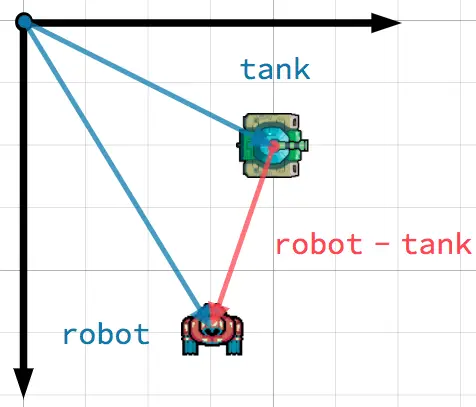
V tomto scénáři máte tank, který chce namířit svou věž na robota. Odečtením pozice tanku od pozice robota dostaneme vektor směřující od tanku k robotovi.

Tip

To find a vector pointing from A to B, use B - A.

Jednotkové vektory

Vektor o velikosti 1 se nazývá jednotkový vektor. Někdy se také označují jako směrové vektory nebo normály Jednotkové vektory jsou užitečné, když potřebujete ponechat směr.

Normalizace

Normalizing a vector means reducing its length to 1 while preserving its direction. This is done by dividing each of its components by its magnitude. Because this is such a common operation, Godot provides a dedicated normalized() method for this:

a = a.normalized()

a = a.Normalized();

Varování

Because normalization involves dividing by the vector's length, you cannot normalize a vector of length 0. Attempting to do so would normally result in an error. In GDScript though, trying to call the normalized() method on a vector of length 0 leaves the value untouched and avoids the error for you.

Odraz

Běžným použitím jednotkových vektorů je indikace normál. Normálové vektory jsou jednotkové vektory kolmé k povrchu, určující jeho směr. Běžně se používají pro osvětlení, kolize a další operace zahrnující povrchy.

Představme si například, že máme pohybující se míč, který chceme odrazit od zdi nebo jiného předmětu:

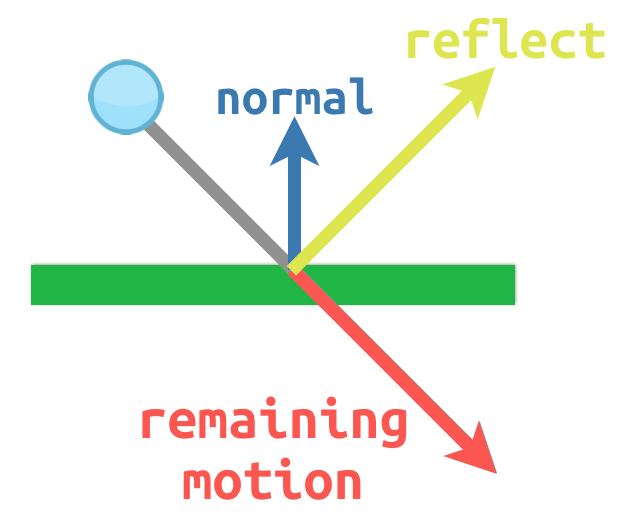
The surface normal has a value of (0, -1) because this is a horizontal surface. When the ball collides, we take its remaining motion (the amount left over when it hits the surface) and reflect it using the normal. In Godot, there is a bounce() method to handle this. Here is a code example of the above diagram using a CharacterBody2D:

var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
    var reflect = collision.get_remainder().bounce(collision.get_normal())
    velocity = velocity.bounce(collision.get_normal())
    move_and_collide(reflect)

KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
    var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
    _velocity = _velocity.Bounce(collision.GetNormal());
    MoveAndCollide(reflect);
}

Skalární součin

Skalární součin je jeden z nejdůležitějších pojmů vektorové matematiky, ale často je nepochopen. Skalární součin je operace dvou vektorů, která vrací skalár. Oproti vektoru, který obsahuje velikost a směr, je hodnota skaláru pouze velikost.

Vzorec pro skalární součin má dvě běžné formy:

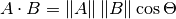
a

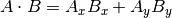
The mathematical notation ||A|| represents the magnitude of vector A, and A_x means the x component of vector A.

However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:

var c = a.dot(b)
var d = b.dot(a)  # These are equivalent.

float c = a.Dot(b);
float d = b.Dot(a);  // These are equivalent.

The dot product is most useful when used with unit vectors, making the first formula reduce to just cos(θ). This means we can use the dot product to tell us something about the angle between two vectors:

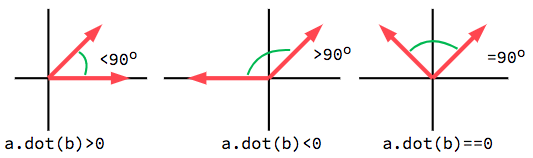
Při použití jednotkových vektorů bude výsledek vždy mezi -1 (180°) a 1 (0°).

Směřování

Tuto skutečnost můžeme využít ke zjištění, zda objekt směřuje k jinému objektu. Na schématu níže se hráč P snaží vyhnout zombiím A a B. Mohou vidět hráče při předpokladu, že zorné pole zombií je 180°?

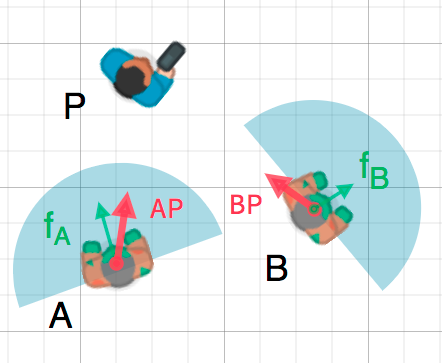
The green arrows fA and fB are unit vectors representing the zombie's facing direction and the blue semicircle represents its field of view. For zombie A, we find the direction vector AP pointing to the player using P - A and normalize it, however, Godot has a helper method to do this called direction_to(). If the angle between this vector and the facing vector is less than 90°, then the zombie can see the player.

V kódu by to vypadalo takto:

var AP = A.direction_to(P)
if AP.dot(fA) > 0:
    print("A sees P!")

var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
    GD.Print("A sees P!");
}

Vektorový součin

Stejně jako skalární součin, tak i vektorový součin je operací dvou vektorů. Výsledkem vektorového součiny je však vektor se směrem kolmým na oba vektory. Jeho velikost závisí na jejich vzájemném úhlu. Pokud jsou dva vektory rovnoběžné, výsledkem jejich vektorového součinu bude nulový vektor.

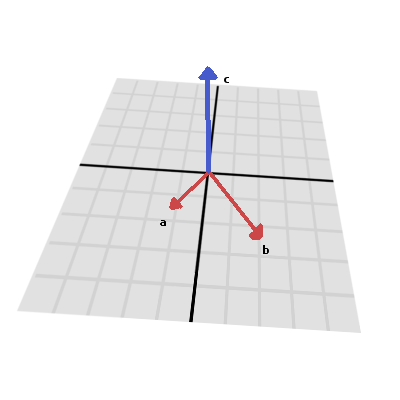
Vektorový součin se vypočítá nějak takto:

var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)

var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);

With Godot, you can use the built-in Vector3.cross() method:

var c = a.cross(b)

var c = a.Cross(b);

The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.

Poznámka

U vektorového součinu záleží na pořadí. a.cross(b) nedává stejný výsledek jako b.cross(a). Výsledné vektory mají opačné směry.

Výpočet normál

One common use of cross products is to find the surface normal of a plane or surface in 3D space. If we have the triangle ABC we can use vector subtraction to find two edges AB and AC. Using the cross product, AB × AC produces a vector perpendicular to both: the surface normal.

Zde je funkce pro výpočet normály trojúhelníku:

func get_triangle_normal(a, b, c):
    # Find the surface normal given 3 vertices.
    var side1 = b - a
    var side2 = c - a
    var normal = side1.cross(side2)
    return normal

Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
    // Find the surface normal given 3 vertices.
    var side1 = b - a;
    var side2 = c - a;
    var normal = side1.Cross(side2);
    return normal;
}

Ukazování k cíli

Ve výše uvedené části o skalárním součinu jsme viděli, jak nalezneme úhel mezi dvěma vektory. Ve 3D však tato informace nestačí. Potřebujeme také vědět, kolem které osy se otáčet. Můžeme to zjistit výpočtem vektorového součinu aktuálního směru a cílového směru. Výsledným kolmým vektorem je osa rotace.

Více informací

Další informace o použití vektorové matematiky v Godot naleznete v následujících článcích: