Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Usando transformaciones 3D¶
Introducción¶
Si nunca has hecho juegos 3D antes, trabajar con rotaciones en tres dimensiones puede resultar confuso al principio. Viniendo de 2D, la forma natural de pensar es como "Oh, es como rotar en 2D, excepto que ahora las rotaciones ocurren en X, Y y Z ".
Al principio esto puede parecer fácil y para los juegos simples, esta forma de pensar puede incluso ser suficiente. Por desgracia, con frecuencia es incorrecto.
Los ángulos en tres dimensiones se denominan comúnmente "Ángulos de Euler".
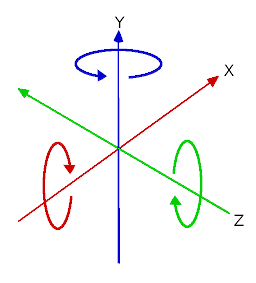
Los ángulos de Euler fueron introducidos por el matemático Leonhard Euler a principios del siglo XVIII.

Esta forma de representar rotaciones en 3D fue revolucionaria en su momento, pero tiene varios defectos cuando se utiliza en el desarrollo de juegos (lo cual es de esperar de un sujeto con un sombrero gracioso). La idea de este documento es explicar por qué, así como esbozar las mejores prácticas para hacer frente a las transformaciones en la programación de juegos 3D.
Problemas de los ángulos de Euler¶
Si bien puede parecer intuitivo que cada eje tenga una rotación, la realidad es que no resulta práctico.
Orden de los ejes¶
La razón principal de esto es que no hay una forma única de construir una orientación desde los ángulos. No hay una función matemática estándar que tome todos los ángulos juntos y produzca una rotación 3D real. La única manera de producir una orientación desde ángulos es girar el objeto ángulo por ángulo, en un orden arbitrario.
Esto podría hacerse rotando primero en X, luego en Y y luego en Z. O bien, se puede rotar primero en Y, luego en Z y finalmente en X. Cualquier método funciona, pero dependiendo del orden, la orientación final del objeto no será necesariamente la misma. De hecho, esto significa que hay varias maneras de construir una orientación desde 3 ángulos diferentes, dependiendo de el orden de las rotaciones.
A continuación se muestra una visualización de los ejes de rotación (en orden X, Y, Z) en un cardán o gimbal en inglés (de Wikipedia). Como se puede ver, la orientación de cada eje depende de la rotación del anterior:
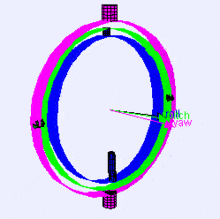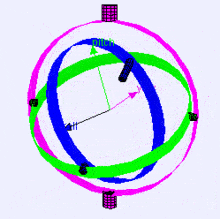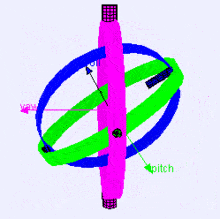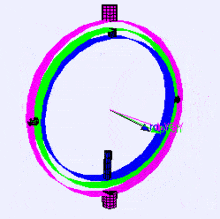
Puede que te preguntes cómo te afecta esto. Veamos un ejemplo práctico:
Imagina que estás trabajando en el control de un juego en primera persona (FPS). Mover el ratón a la izquierda y a la derecha controla el ángulo de visión paralelo al suelo, mientras que moverlo hacia arriba y hacia abajo mueve la vista del jugador hacia arriba y hacia abajo.
En este caso para conseguir el efecto deseado, la rotación se debe aplicar primero en el eje Y (en este caso "arriba", ya que Godot utiliza una orientación "Y-Up"), seguido de la rotación en el eje X.

Si primero aplicáramos la rotación en el eje X, y luego en el eje Y, el resultado no sería el deseado:

Dependiendo del tipo de juego o efecto deseado, el orden en el que desea que se apliquen las rotaciones de los ejes puede variar. Por lo tanto, la aplicación de rotaciones en X, Y y Z no es suficiente: también es necesario un orden de rotación.
Interpolación¶
Otro problema con el uso de los ángulos de Euler es la interpolación. Imagina que quieres hacer la transición entre dos cámaras diferentes o posiciones enemigas (incluyendo rotaciones). Una manera lógica de acercarse a esto es interpolar los ángulos de una posición a otra. Uno esperaría que se viera así:

Pero esto no siempre tiene el resultado esperado cuando se utilizan ángulos:

¡La cámara giró en la dirección opuesta!
Hay algunas razones por las que esto puede suceder:
Las rotaciones no se mapean linealmente a la orientación, por lo que interpolarlas no siempre da como resultado la trayectoria más corta (es decir, pasar de
270a0grados no es lo mismo que pasar de270a360, aunque los ángulos sean equivalentes).El bloqueo del cardán está en juego (el primer y último eje de rotación se alinean, por lo que se pierde un grado de libertad). Consulta la página de Wikipedia en Bloqueo del cardán para obtener una explicación más detallada acerca de este problema.
Di no a los ángulos de Euler¶
The result of all this is that you should not use the rotation property of Node3D nodes in Godot for games. It's there to be used mainly in the editor, for coherence with the 2D engine, and for simple rotations (generally just one axis, or even two in limited cases). As much as you may be tempted, don't use it.
En cambio, hay una mejor manera de resolver estos problemas de rotación.
Introducción a Transforms¶
Godot uses the Transform3D datatype for orientations. Each Node3D node contains a transform property which is relative to the parent's transform, if the parent is a Node3D-derived type.
También es posible acceder a la transformación de coordenadas del mundo a través de la propiedad global_transform.
Un transform (o matriz de transformación) tiene una Basis (sub-propiedad transform.basis), que consiste en tres vectores Vector3. Se accede a ellos a través de la propiedad transform.basis y se puede acceder a ellos directamente a través de transform.basis.x, transform.basis.y ``, y ``transformar.basis.z. Cada vector apunta en la dirección en la que se ha girado cada eje, por lo que describe eficazmente la rotación total del nodo. La escala (siempre que sea uniforme) también se puede calcular a partir de la longitud de los ejes. Una basis también puede ser interpretada como una matriz 3x3 y usada como transform.basis[x][y].
Una base por defecto (sin modificar) es similar a:
var basis = Basis()
# Contains the following default values:
basis.x = Vector3(1, 0, 0) # Vector pointing along the X axis
basis.y = Vector3(0, 1, 0) # Vector pointing along the Y axis
basis.z = Vector3(0, 0, 1) # Vector pointing along the Z axis
// Due to technical limitations on structs in C# the default
// constructor will contain zero values for all fields.
var defaultBasis = new Basis();
GD.Print(defaultBasis); // prints: ((0, 0, 0), (0, 0, 0), (0, 0, 0))
// Instead we can use the Identity property.
var identityBasis = Basis.Identity;
GD.Print(identityBasis.X); // prints: (1, 0, 0)
GD.Print(identityBasis.Y); // prints: (0, 1, 0)
GD.Print(identityBasis.Z); // prints: (0, 0, 1)
// The Identity basis is equivalent to:
var basis = new Basis(Vector3.Right, Vector3.Up, Vector3.Back);
GD.Print(basis); // prints: ((1, 0, 0), (0, 1, 0), (0, 0, 1))
Esto también es similar a una matriz de identidad 3x3.
Siguiendo la convención OpenGL, X es el eje horizontal (Right), Y es el eje vertical (Up) y Z es el eje frontal (Forward).
Junto con la base, una transformación también tiene un origen. Este es un Vector3 especificando cuán lejos del origen real (0, 0, 0) se encuentra esta transformación. Combinando la base con el origen, una transformación representa eficientemente un desplazamiento, rotación y escala únicos en el espacio.
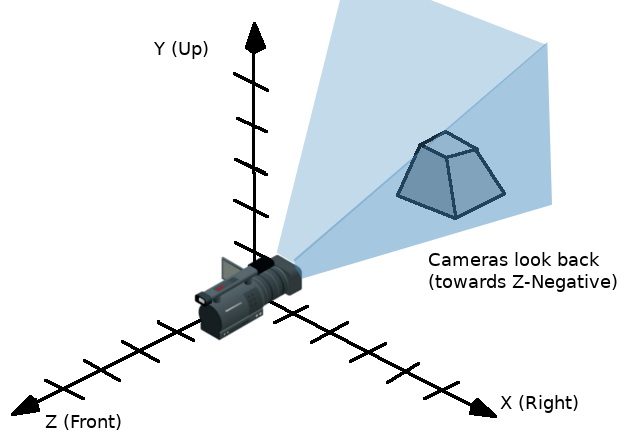
Una forma de visualizar una transformación es mirar el gizmo 3D de un objeto mientras está en modo "espacio local".

Las flechas del Gizmo muestran los ejes X. Y y Z (En rojo, verde, y azul respectivamente) de la basis, mientras que el centro del Gizmo está en el origen del objeto.

Para más información sobre las matemáticas de vectores y transformaciones, por favor lee los tutoriales Matemáticas vectoriales.
Manipulando Transforms¶
Por supuesto, las transformaciones no son tan sencillas de manipular como los ángulos y tienen sus propios problemas.
Es posible rotar un transformación, ya sea multiplicando su base por otra (esto es llamado acumulación), o usando los métodos de rotación.
var axis = Vector3(1, 0, 0) # Or Vector3.RIGHT
var rotation_amount = 0.1
# Rotate the transform around the X axis by 0.1 radians.
transform.basis = Basis(axis, rotation_amount) * transform.basis
# shortened
transform.basis = transform.basis.rotated(axis, rotation_amount)
Transform3D transform = Transform;
Vector3 axis = new Vector3(1, 0, 0); // Or Vector3.Right
float rotationAmount = 0.1f;
// Rotate the transform around the X axis by 0.1 radians.
transform.Basis = new Basis(axis, rotationAmount) * transform.Basis;
// shortened
transform.Basis = transform.Basis.Rotated(axis, rotationAmount);
Transform = transform;
A method in Node3D simplifies this:
# Rotate the transform around the X axis by 0.1 radians.
rotate(Vector3(1, 0, 0), 0.1)
# shortened
rotate_x(0.1)
// Rotate the transform around the X axis by 0.1 radians.
Rotate(new Vector3(1, 0, 0), 0.1f);
// shortened
RotateX(0.1f);
Esto rota el nodo relativo al nodo padre.
Para rotar en relación con el espacio del objeto (la transformación propia del nodo) se utiliza lo siguiente:
# Rotate around the object's local X axis by 0.1 radians.
rotate_object_local(Vector3(1, 0, 0), 0.1)
// Rotate around the object's local X axis by 0.1 radians.
RotateObjectLocal(new Vector3(1, 0, 0), 0.1f);
Errores de precisión¶
Si se realizan operaciones consecutivas con transformaciones, se producirá una pérdida de precisión debido a un error de punto flotante. Esto significa que la escala de cada eje puede que ya no sea exactamente 1.0, y puede que no sea exactamente 90 grados entre sí.
Si se rota una transformación en cada cuadro, eventualmente comenzará a deformarse con el tiempo. Esto es inevitable.
Hay dos maneras diferentes de resolver esto. La primera es ortonormalizar la transformación después de algún tiempo (tal vez una vez por fotograma si se modifica cada fotograma):
transform = transform.orthonormalized()
transform = transform.Orthonormalized();
Esto hará que todos los ejes tengan de nuevo una longitud de 1.0 y estén a 90 grados entre sí. Sin embargo, cualquier escala aplicada a la transformación se perderá.
It is recommended you not scale nodes that are going to be manipulated; scale their children nodes instead (such as MeshInstance3D). If you absolutely must scale the node, then re-apply it at the end:
transform = transform.orthonormalized()
transform = transform.scaled(scale)
transform = transform.Orthonormalized();
transform = transform.Scaled(scale);
Obteniendo información¶
Podrías estar pensando en este momento: "Bueno, ¿pero cómo obtengo los ángulos de una transformación?" La respuesta de nuevo es: no se puede. Debes hacer todo lo posible para dejar de pensar en ángulos.
Imagina que necesitas disparar una bala en la dirección en la que tu jugador está mirando. Sólo usa el eje delantero (o forward, comúnmente Z o -Z).
bullet.transform = transform
bullet.speed = transform.basis.z * BULLET_SPEED
bullet.Transform = transform;
bullet.LinearVelocity = transform.Basis.Z * BulletSpeed;
¿El enemigo está mirando al jugador? Usa el producto escalar para esto (ver el tutorial Matemáticas vectoriales para una explicación del producto escalar):
# Get the direction vector from player to enemy
var direction = enemy.transform.origin - player.transform.origin
if direction.dot(enemy.transform.basis.z) > 0:
enemy.im_watching_you(player)
// Get the direction vector from player to enemy
Vector3 direction = enemy.Transform.Origin - player.Transform.Origin;
if (direction.Dot(enemy.Transform.Basis.Z) > 0)
{
enemy.ImWatchingYou(player);
}
Ataque a la izquierda:
# Remember that +X is right
if Input.is_action_pressed("strafe_left"):
translate_object_local(-transform.basis.x)
// Remember that +X is right
if (Input.IsActionPressed("strafe_left"))
{
TranslateObjectLocal(-Transform.Basis.X);
}
Salto:
# Keep in mind Y is up-axis
if Input.is_action_just_pressed("jump"):
velocity.y = JUMP_SPEED
move_and_slide()
// Keep in mind Y is up-axis
if (Input.IsActionJustPressed("jump"))
velocity.Y = JumpSpeed;
MoveAndSlide();
Todos los comportamientos comunes y la lógica se pueden hacer sólo con vectores.
Asignando valores¶
Hay, por supuesto, casos en los que se desea establecer la información como una transformación. Imagina un controlador de primera persona o una cámara en órbita. Estos se hacen definitivamente usando ángulos, porque quieres que las transformaciones ocurran en un orden específico.
For such cases, keep the angles and rotations outside the transform and set them every frame. Don't try to retrieve and reuse them because the transform is not meant to be used this way.
Un ejemplo de cómo mirar alrededor, al estilo FPS:
# accumulators
var rot_x = 0
var rot_y = 0
func _input(event):
if event is InputEventMouseMotion and event.button_mask & 1:
# modify accumulated mouse rotation
rot_x += event.relative.x * LOOKAROUND_SPEED
rot_y += event.relative.y * LOOKAROUND_SPEED
transform.basis = Basis() # reset rotation
rotate_object_local(Vector3(0, 1, 0), rot_x) # first rotate in Y
rotate_object_local(Vector3(1, 0, 0), rot_y) # then rotate in X
// accumulators
private float _rotationX = 0f;
private float _rotationY = 0f;
public override void _Input(InputEvent @event)
{
if (@event is InputEventMouseMotion mouseMotion)
{
// modify accumulated mouse rotation
_rotationX += mouseMotion.Relative.X * LookAroundSpeed;
_rotationY += mouseMotion.Relative.Y * LookAroundSpeed;
// reset rotation
Transform3D transform = Transform;
transform.Basis = Basis.Identity;
Transform = transform;
RotateObjectLocal(Vector3.Up, _rotationX); // first rotate about Y
RotateObjectLocal(Vector3.Right, _rotationY); // then rotate about X
}
}
Como puedes ver, en estos casos es aún más simple mantener la rotación fuera, y luego usar el transform como orientación final.
Interpolando con quaternions¶
La interpolación entre dos transformaciones se puede hacer eficientemente con quaternions. Para más información sobre cómo funcionan los quaternions, puedes consultar otros sitios de Internet. Para uso práctico, es suficiente entender que su uso principal es hacer una interpolación de ruta más cercana. Como en el caso anterior, si tiene dos rotaciones, un quaternion permitirá suavemente la interpolación entre ellas usando el eje más cercano.
Convertir una rotación a quaternion es sencillo.
# Convert basis to quaternion, keep in mind scale is lost
var a = Quaternion(transform.basis)
var b = Quaternion(transform2.basis)
# Interpolate using spherical-linear interpolation (SLERP).
var c = a.slerp(b,0.5) # find halfway point between a and b
# Apply back
transform.basis = Basis(c)
// Convert basis to quaternion, keep in mind scale is lost
var a = transform.Basis.GetQuaternion();
var b = transform2.Basis.GetQuaternion();
// Interpolate using spherical-linear interpolation (SLERP).
var c = a.Slerp(b, 0.5f); // find halfway point between a and b
// Apply back
transform.Basis = new Basis(c);
The Quaternion type reference has more information on the datatype (it can also do transform accumulation, transform points, etc., though this is used less often). If you interpolate or apply operations to quaternions many times, keep in mind they need to be eventually normalized. Otherwise, they will also suffer from numerical precision errors.
Los quaternions son útiles cuando se realizan interpolaciones de cámara/trayectoria/etc., ya que el resultado será siempre correcto y suave.
Los Transforms son tus amigos¶
Para la mayoría de los principiantes, acostumbrarse a trabajar con transformaciones puede llevar algún tiempo. Sin embargo, una vez que te acostumbres a ellos, apreciarás su simplicidad y poder.
No dudes en pedir ayuda sobre este tema en cualquiera de las comunidades en línea de Godot y, una vez que tengas suficiente experiencia ¡ayuda a los demás!