Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Matrices y transformaciones¶
Introducción¶
Antes de leer este tutorial, recomendamos leer y entender el tutorial anterior Matemáticas vectoriales, ya que éste requiere conocimiento sobre vectores.
Este tutorial trata sobre las transformaciones y cómo las representamos en Godot usando matrices. No es una guía completa y detallada de las matrices. Las transformaciones se aplican la mayoría de las veces como traslación, rotación y escala, por lo que nos centraremos en cómo representarlas con matrices.
La mayor parte de esta guía se centra en el 2D, usando Transform2D y Vector2, pero la forma en que funcionan las cosas en el 3D es muy similar.
Nota
Como se mencionó en el tutorial anterior, es importante recordar que en Godot, el eje Y apunta abajo en 2D. Esto es lo opuesto a como la mayoría de las escuelas enseñan álgebra lineal, con el eje Y apuntando hacia arriba.
Nota
La convención es que el eje X es rojo, el eje Y es verde y el eje Z es azul. Este tutorial está codificado por colores para coincidir con estas convenciones, pero también representaremos el vector de origen con un color azul.
Componentes de la matriz y la matriz de Identidad¶
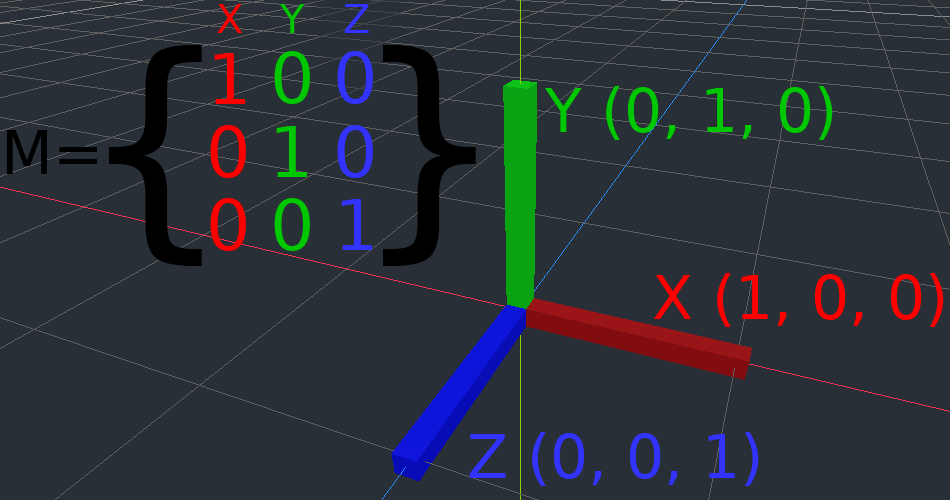
La matriz de identidad representa una transformación sin traslación, sin rotación y sin escala. Empecemos por mirar la matriz de identidad y cómo sus componentes se relacionan con la forma en que aparece visualmente.
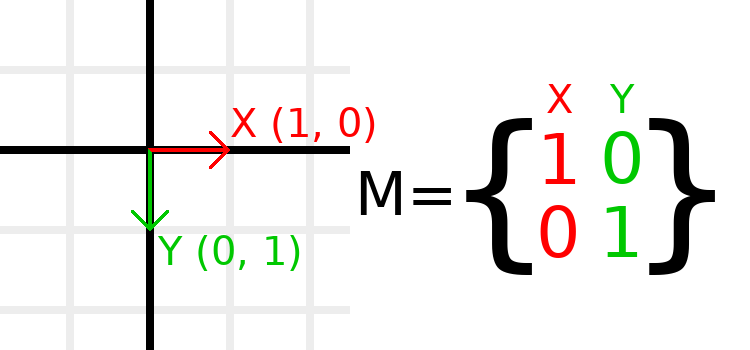
Las matrices tienen filas y columnas, y una matriz de transformación tiene convenciones específicas sobre lo que hace cada una.
En la imagen de arriba, podemos ver que el vector X rojo está representado por la primera columna de la matriz, y el vector Y verde está igualmente representado por la segunda columna. Un cambio en las columnas cambiará estos vectores. Veremos cómo pueden ser manipulados en los próximos ejemplos.
No debes preocuparte por manipular las filas directamente, ya que normalmente trabajamos con columnas. Sin embargo, se puede pensar en las filas de la matriz como mostrando qué vectores contribuyen a moverse en una dirección determinada.
When we refer to a value such as t.x.y, that's the Y component of
the X column vector. In other words, the bottom-left of the matrix.
Similarly, t.x.x is top-left, t.y.x is top-right, and t.y.y
is bottom-right, where t is the Transform2D.
Escalando la matriz de transformación¶
La aplicación de una escala es una de las operaciones más fáciles de entender. Empecemos colocando el logo de Godot debajo de nuestros vectores para que podamos ver los efectos en un objeto:
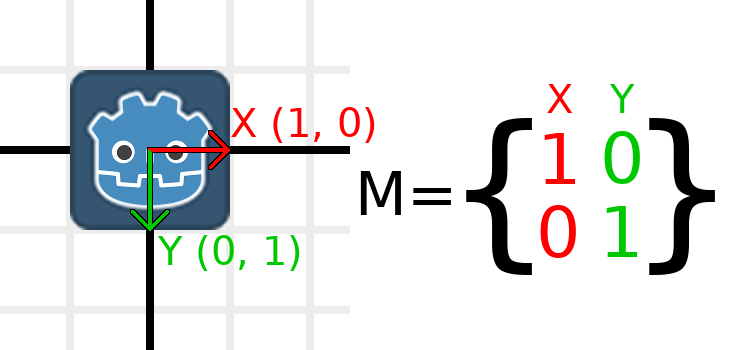
Ahora, para escalar la matriz, todo lo que tenemos que hacer es multiplicar cada componente por la escala que queremos. Escalémosla por 2. 1 por 2 se convierte en 2, y 0 por 2 se convierte en 0, así que terminamos con esto:
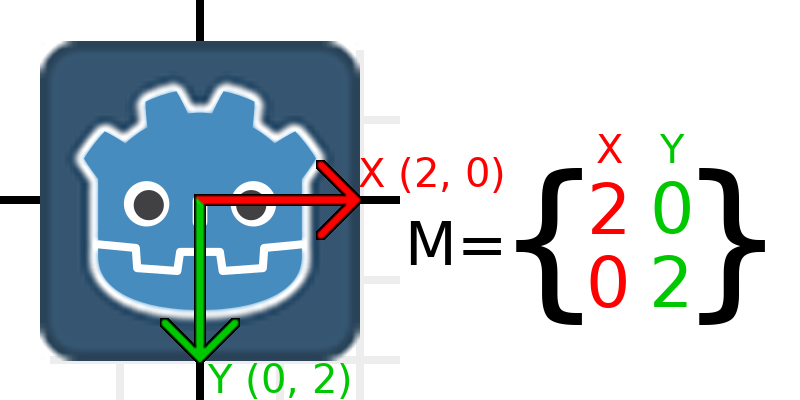
To do this in code, we multiply each of the vectors:
var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Scale
t.X *= 2;
t.Y *= 2;
Transform = t; // Change the node's transform to what we calculated.
Si quisiéramos devolverlo a su escala original, podemos multiplicar cada componente por 0.5. Eso es más o menos todo lo que hay que hacer para escalar una matriz de transformación.
To calculate the object's scale from an existing transformation
matrix, you can use length() on each of the column vectors.
Nota
In actual projects, you can use the scaled()
method to perform scaling.
Rotando la matriz de transformación¶
Empezaremos de la misma manera que antes, con el logo de Godot debajo de la matriz de identidad:

Como ejemplo, digamos que queremos girar nuestro logo de Godot en el sentido de las agujas del reloj en 90 grados. Ahora mismo el eje X apunta a la derecha y el eje Y apunta hacia abajo. Si lo rotamos en nuestra cabeza, lógicamente veríamos que el nuevo eje X apunta hacia abajo y el nuevo eje Y hacia la izquierda.
Puedes imaginar que tomas el logo de Godot y sus vectores, y luego lo giras alrededor del centro. Dondequiera que termines de girar, la orientación de los vectores determina lo que es la matriz.
We need to represent "down" and "left" in normal coordinates,
so means we'll set X to (0, 1) and Y to (-1, 0). These are
also the values of Vector2.DOWN and Vector2.LEFT.
When we do this, we get the desired result of rotating the object:
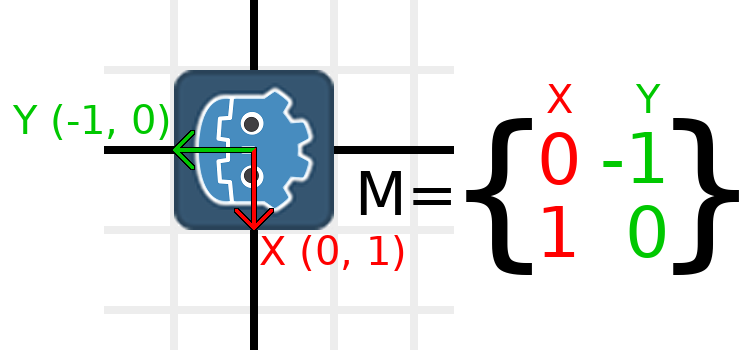
Si tiene problemas para entender lo anterior, intente este ejercicio: Corte un cuadrado de papel, dibuju los vectores X e Y encima de él, colócalo en un papel cuadriculado, luego gíralo y anota los puntos finales.
Para realizar la rotación en el código, necesitamos ser capaces de calcular los valores de forma programada. Esta imagen muestra las fórmulas necesarias para calcular la matriz de transformación desde un ángulo de rotación. No te preocupes si esta parte parece complicada, te prometo que es lo más difícil que necesitas saber.
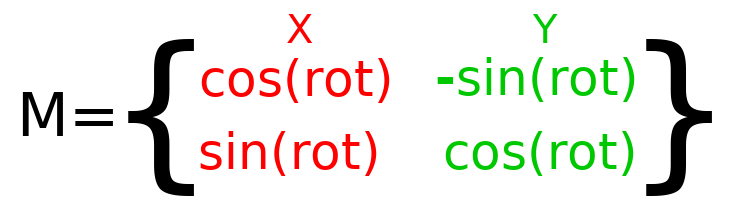
Nota
Godot representa todas las rotaciones con radianes, no grados. Un giro completo es TAU o PI*2 radianes, y un cuarto de giro de 90 grados es TAU/4 o PI/2 radianes. Trabajar con TAU usualmente resulta en un código más legible.
Nota
Dato curioso: Además de que la Y está abajo en Godot, la rotación se representa en el sentido de las agujas del reloj. Esto significa que todas las funciones matemáticas y de trigonometría se comportan igual que en un sistema de sentido de las horas de un reloj con la Y hacia arriba, ya que estas diferencias "se cancelan". Se puede pensar que las rotaciones en ambos sistemas son "de X a Y".
In order to perform a rotation of 0.5 radians (about 28.65 degrees), we plug in a value of 0.5 to the formula above and evaluate to find what the actual values should be:
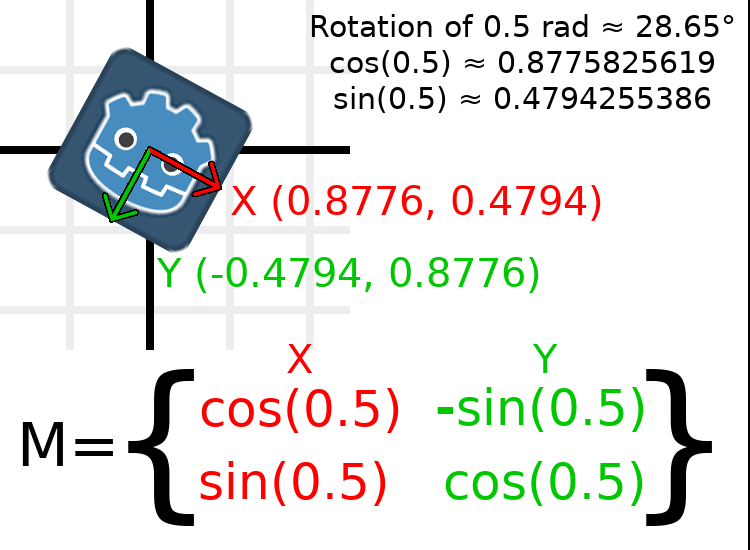
Así es como se haría en código (colocar el script en un Nodo2D):
var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we calculated.
float rot = 0.5f; // The rotation to apply.
Transform2D t = Transform2D.Identity;
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
Transform = t; // Change the node's transform to what we calculated.
To calculate the object's rotation from an existing transformation
matrix, you can use atan2(t.x.y, t.x.x), where t is the Transform2D.
Nota
In actual projects, you can use the rotated()
method to perform rotations.
La base de la matriz de transformación¶
So far we have only been working with the x and y, vectors, which
are in charge of representing rotation, scale, and/or shearing
(advanced, covered at the end). The X and Y vectors are together
called the basis of the transformation matrix. The terms "basis"
and "basis vectors" are important to know.
You might have noticed that Transform2D actually
has three Vector2 values: x, y, and origin.
The origin value is not part of the basis, but it is part of the
transform, and we need it to represent position. From now on we'll
keep track of the origin vector in all examples. You can think of
origin as another column, but it's often better to think of it as
completely separate.
Note that in 3D, Godot has a separate Basis structure for holding the three Vector3 values of the basis, since the code can get complex and it makes sense to separate it from Transform3D (which is composed of one Basis and one extra Vector3 for the origin).
Trasladando la matriz de transformación¶
Changing the origin vector is called translating the transformation
matrix. Translating is basically a technical term for "moving" the
object, but it explicitly does not involve any rotation.
Trabajemos con un ejemplo para ayudar a entender esto. Empezaremos con la transformación de identidad como la última vez, excepto que esta vez seguiremos el vector de origen.
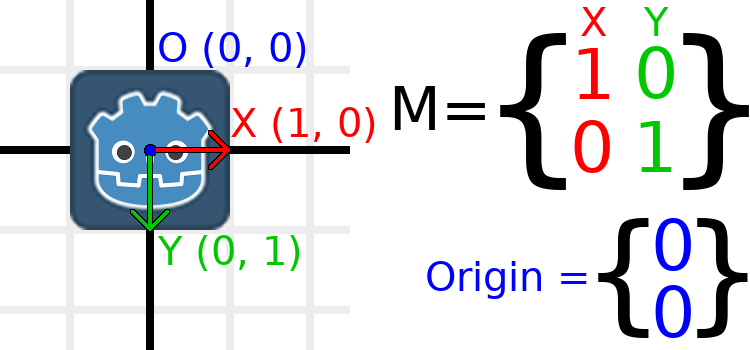
If we want to move the object to a position of (1, 2), we need
to set its origin vector to (1, 2):
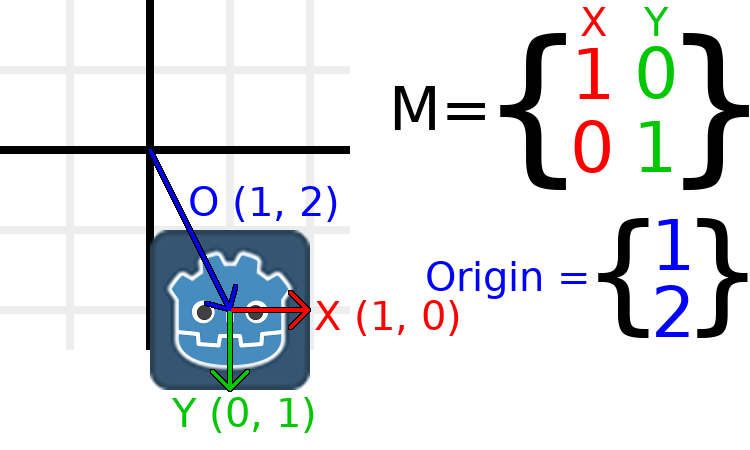
There is also a translated() method, which performs a different
operation to adding or changing origin directly. The translated()
method will translate the object relative to its own rotation.
For example, an object rotated 90 degrees clockwise will move to
the right when translated() with Vector2.UP.
Nota
El 2D de Godot usa coordenadas basadas en píxeles, por lo que en los proyectos reales querrás transladarlos por cientos de unidades.
Poniendo todo junto¶
We're going to apply everything we mentioned so far onto one transform. To follow along, create a project with a Sprite2D node and use the Godot logo for the texture resource.
Pongamos la traslación a (350, 150), rotar por -0,5 rad, y escalar por 3. He publicado una captura de pantalla, y el código para reproducirla, ¡pero os animo a intentar reproducir la captura de pantalla sin mirar el código!
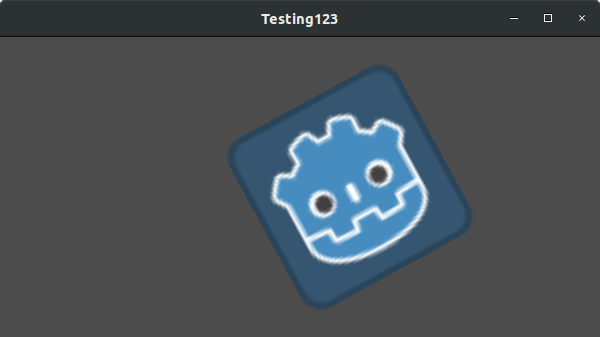
var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Translation
t.Origin = new Vector2(350, 150);
// Rotation
float rot = -0.5f; // The rotation to apply.
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
// Scale
t.X *= 3;
t.Y *= 3;
Transform = t; // Change the node's transform to what we calculated.
Inclinando la matrix transformada (Avanzado)¶
Nota
Si sólo buscas cómo usar las matrices de transformación, no dudes en saltarte esta sección del tutorial. Esta sección explora un aspecto poco común de las matrices de transformación con el propósito de construir una comprensión de las mismas.
Node2D provides a shearing property out of the box.
Habrá notado que una transformación tiene más grados de libertad que la combinación de las acciones anteriores. La base de una matriz de transformación 2D tiene cuatro números totales en dos clase_Vector2 valores, mientras que un valor de rotación y un Vector2 para la escala sólo tiene 3 números. El concepto de alto nivel para el grado de libertad que falta se llama shearing.
Normalmente, siempre tendrá los vectores base perpendiculares entre sí. Sin embargo, la inclinación puede ser útil en algunas situaciones, y comprender la inclinación le ayuda a entender cómo funcionan las transformaciones.
Para mostrar visualmente cómo se verá, superpongamos un grid sobre el logo de Godot:
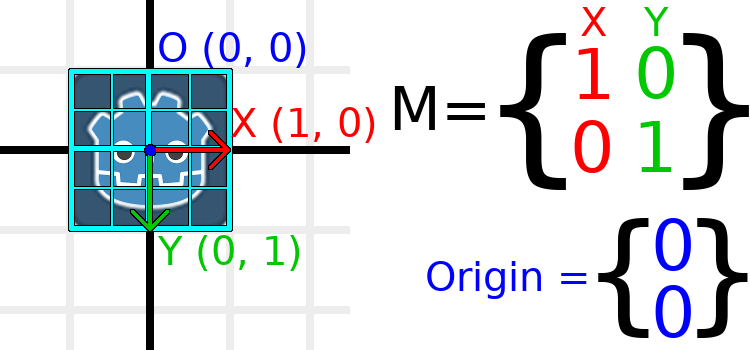
Cada punto de este grid se obtiene sumando los vectores base. La esquina inferior derecha es X + Y, mientras que la esquina superior derecha es X - Y. Si cambiamos los vectores base, toda el grid se mueve con el, ya que la grid está compuesta de los vectores base. Todas las líneas del grid que son actualmente paralelas permanecerán paralelas sin importar los cambios que hagamos en los vectores base.
Como ejemplo, pongamos Y a (1, 1):
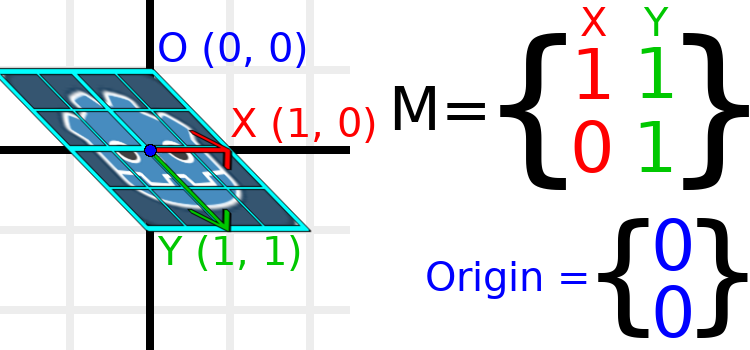
var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Shear by setting Y to (1, 1)
t.Y = Vector2.One;
Transform = t; // Change the node's transform to what we calculated.
Nota
No puedes establecer los valores crudos de un Transform2D en el editor, así que debes usar código si quieres inclinar el objeto.
Debido a que los vectores ya no son perpendiculares, el objeto ha sido inclinado. El centro inferior del grid, que es (0, 1) con respecto a sí mismo, se encuentra ahora en una posición mundial de (1, 1).
Las coordenadas intra-objeto se llaman coordenadas UV en las texturas, así que tomemos prestada esa terminología para aquí. Para encontrar la posición del mundo desde una posición relativa, la fórmula es U * X + V * Y, donde U y V son números y X e Y son los vectores base.
La esquina inferior derecha del grid, que siempre está en la posición UV de (1, 1), está en la posición mundial de (2, 1), que se calcula a partir de X*1 + Y*1, que es (1, 0) + (1, 1), o (1 + 1, 0 + 1), o (2, 1). Esto coincide con nuestra observación de dónde está la esquina inferior derecha de la imagen.
De manera similar, la esquina superior derecha del grid, que siempre está en la posición UV de (1, -1), está en la posición mundial de (0, -1), que se calcula a partir de X*1 + Y*-1, que es (1, 0) - (1, 1), o (1 - 1, 0 - 1), o (0, -1). Esto concuerda con nuestra observación de dónde está la esquina superior derecha de la imagen.
Esperemos que ahora entiendas completamente cómo una matriz de transformación afecta al objeto, y la relación entre los vectores base y cómo los "UV" o "intra-coordinados" del objeto han cambiado su posición en el mundo.
Nota
En Godot, toda la matemática de transformación se hace en relación con el nodo padre. Cuando nos referimos a la "posición del mundo", eso sería relativo al padre del nodo, si el nodo tuviera un padre.
Si desea una explicación adicional, debería ver el excelente video de 3Blue1Brown sobre las transformaciones lineales: https://www.youtube.com/watch?v=kYB8IZa5AuE
Aplicaciones prácticas de las transformaciones¶
In actual projects, you will usually be working with transforms inside transforms by having multiple Node2D or Node3D nodes parented to each other.
However, it's useful to understand how to manually calculate the values we need. We will go over how you could use Transform2D or Transform3D to manually calculate transforms of nodes.
Convertir las posiciones entre las transformaciones¶
Hay muchos casos en los que se querría convertir una posición dentro y fuera de una transformación. Por ejemplo, si tienes una posición relativa al jugador y te gustaría encontrar la posición mundial (parentesco con los padres), o si tienes una posición mundial y quieres saber dónde está relativa al jugador.
We can find what a vector relative to the player would be defined in
world space as using the * operator:
# World space vector 100 units below the player.
print(transform * Vector2(0, 100))
// World space vector 100 units below the player.
GD.Print(Transform * new Vector2(0, 100));
And we can use the * operator in the opposite order to find a what world
space position would be if it was defined relative to the player:
# Where is (0, 100) relative to the player?
print(Vector2(0, 100) * transform)
// Where is (0, 100) relative to the player?
GD.Print(new Vector2(0, 100) * Transform);
Nota
Si se sabe de antemano que la transformación está posicionada en (0, 0), se pueden utilizar los métodos "base_xform" o "base_xform_inv" en su lugar, que se saltan el tratar con la translación.
Mover un objeto en relación a sí mismo¶
Una operación común, sobre todo en los juegos 3D, es mover un objeto relativo a sí mismo. Por ejemplo, en los juegos de disparos en primera persona, querrías que el personaje se moviera hacia adelante (eje -Z) cuando presionas W.
Since the basis vectors are the orientation relative to the parent, and the origin vector is the position relative to the parent, we can add multiples of the basis vectors to move an object relative to itself.
Este código mueve un objeto 100 unidades a su propio derecho:
transform.origin += transform.x * 100
Transform2D t = Transform;
t.Origin += t.X * 100;
Transform = t;
Para moverse en 3D, necesitarías reemplazar "x" por "base.x".
Nota
In actual projects, you can use translate_object_local in 3D
or move_local_x and move_local_y in 2D to do this.
Aplicando transformaciones sobre transformaciones¶
Una de las cosas más importantes que hay que saber sobre las transformaciones es cómo se pueden usar varias de ellas juntas. La transformación de un nodo padre afecta a todos sus hijos. Diseccionemos un ejemplo.
En esta imagen, el nodo hijo tiene un "2" después de los nombres de los componentes para distinguirlos del nodo padre. Puede parecer un poco abrumador con tantos números, pero recuerde que cada número se muestra dos veces (junto a las flechas y también en las matrices), y que casi la mitad de los números son cero.
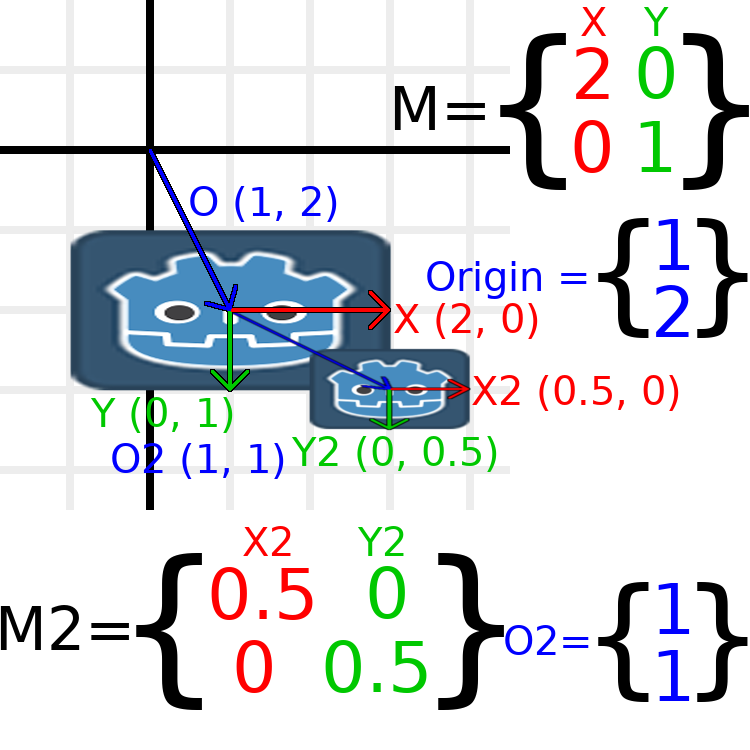
Las únicas transformaciones que ocurren aquí son que al nodo padre se le ha dado una escala de (2, 1), al hijo se le ha dado una escala de (0.5, 0.5), y a ambos nodos se les ha dado posiciones.
All child transformations are affected by the parent transformations.
The child has a scale of (0.5, 0.5), so you would expect it to be
a 1:1 ratio square, and it is, but only relative to the parent.
The child's X vector ends up being (1, 0) in world space, because
it is scaled by the parent's basis vectors.
Similarly, the child node's origin vector is set to (1, 1), but this
actually moves it (2, 1) in world space, due to the parent node's
basis vectors.
Para calcular manualmente la transformación espacial del mundo de un hijo, este es el código que usaríamos:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y
# Change the node's transform to what we calculated.
transform = Transform2D(basis_x, basis_y, origin)
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Calculate the child's world space transform
// origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
Vector2 origin = parent.X * child.Origin.X + parent.Y * child.Origin.Y + parent.Origin;
// basisX = (2, 0) * 0.5 + (0, 1) * 0 = (0.5, 0)
Vector2 basisX = parent.X * child.X.X + parent.Y * child.X.Y;
// basisY = (2, 0) * 0 + (0, 1) * 0.5 = (0.5, 0)
Vector2 basisY = parent.X * child.Y.X + parent.Y * child.Y.Y;
// Change the node's transform to what we calculated.
Transform = new Transform2D(basisX, basisY, origin);
In actual projects, we can find the world transform of the child by
applying one transform onto another using the * operator:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Change the node's transform to what would be the child's world transform.
transform = parent * child
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Change the node's transform to what would be the child's world transform.
Transform = parent * child;
Nota
¡Al multiplicar las matrices, el orden importa! No las mezcles.
Por último, la aplicación de la transformación de la identidad siempre hará nada.
Si desea una explicación adicional, debería ver el excelente vídeo de 3Blue1Brown sobre la composición de la matriz: https://www.youtube.com/watch?v=XkY2DOUCWMU
Invirtiendo la matriz de transformación¶
The "affine_inverse" function returns a transform that "undoes" the previous transform. This can be useful in some situations. Let's take a look at a few examples.
Multiplicar una transformación inversa por la transformación normal deshace todas las transformaciones:
var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.
Transform2D ti = Transform.AffineInverse();
Transform2D t = ti * Transform;
// The transform is the identity transform.
Transforming a position by a transform and its inverse results in the same position:
var ti = transform.affine_inverse()
position = transform * position
position = ti * position
# The position is the same as before.
Transform2D ti = Transform.AffineInverse();
Position = Transform * Position;
Position = ti * Position;
// The position is the same as before.
¿Cómo funciona todo en 3D?¶
One of the great things about transformation matrices is that they work very similarly between 2D and 3D transformations. All the code and formulas used above for 2D work the same in 3D, with 3 exceptions: the addition of a third axis, that each axis is of type Vector3, and also that Godot stores the Basis separately from the Transform3D, since the math can get complex and it makes sense to separate it.
Todos los conceptos de cómo funciona la traslación, rotación, escala e inclinación en 3D son todos iguales comparados con los de 2D. Para escalar, tomamos cada componente y lo multiplicamos; para rotar, cambiamos donde cada vector base está apuntando; para traducir, manipulamos el origen; y para inclinar, cambiamos los vectores base para que no sean perpendiculares.
Si quieres, es una buena idea jugar con las transformaciones para entender cómo funcionan. Godot te permite editar matrices de transformación 3D directamente desde el inspector. Puedes descargar este proyecto que tiene líneas y cubos de colores para ayudar a visualizar los vectores Basis y el origen tanto en 2D como en 3D: https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform
Nota
You cannot edit Node2D's transform matrix directly in Godot 4.0's inspector. This may be changed in a future release of Godot.
Si desea una explicación adicional, debería ver el excelente vídeo de 3Blue1Brown sobre las transformaciones lineales en 3D: https://www.youtube.com/watch?v=rHLEWRxRGiM
Representando una rotación en 3D (avanzado)¶
La mayor diferencia entre las matrices de transformación 2D y 3D es cómo se representa la rotación por sí misma sin los vectores base.
With 2D, we have an easy way (atan2) to switch between a transformation matrix and an angle. In 3D, rotation is too complex to represent as one number. There is something called Euler angles, which can represent rotations as a set of 3 numbers, however, they are limited and not very useful, except for trivial cases.
In 3D we do not typically use angles, we either use a transformation basis (used pretty much everywhere in Godot), or we use quaternions. Godot can represent quaternions using the Quaternion struct. My suggestion to you is to completely ignore how they work under-the-hood, because they are very complicated and unintuitive.
Sin embargo, si realmente debes saber cómo funciona, aquí hay algunos grandes recursos, que puedes seguir en orden:
https://www.youtube.com/watch?v=mvmuCPvRoWQ