Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Matemática vectorial avanzada¶
Planos¶
El producto punto tiene otra propiedad interesante con los vectores unitarios. Imaginemos que perpendicular a ese vector (y a través del origen) pasa un plano. Los planos dividen todo el espacio en positivo (sobre el plano) y negativo (debajo del plano), y (contrariamente a la creencia popular) también puedes usar sus matemáticas en 2D:
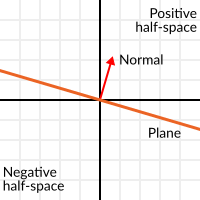
Los vectores unitarios que son perpendiculares a una superficie (por lo tanto, describen la orientación de la superficie) se denominan vectores unitarios normales. Sin embargo, por lo general son sólo abreviados como normales. Las normales aparecen en planos, geometría 3D (para determinar dónde está el revestimiento de cada cara o vértice), etc. Un normal es un vector unitario, pero se le llama normal debido a su uso. (¡Igual que llamamos (0,0) al Origen!).
The plane passes by the origin and the surface of it is perpendicular to the unit vector (or normal). The side towards the vector points to is the positive half-space, while the other side is the negative half-space. In 3D this is exactly the same, except that the plane is an infinite surface (imagine an infinite, flat sheet of paper that you can orient and is pinned to the origin) instead of a line.
Distancia del plano¶
Ahora que está claro lo que es un plano, volvamos al producto punto. El producto punto entre un vector unitario y cualquier punto en el espacio (sí, esta vez hacemos producto de puntos entre vector y posición), devuelve la distancia entre el punto y el plano:
var distance = normal.dot(point)
var distance = normal.Dot(point);
Pero no sólo la distancia absoluta, si el punto está en el semiespacio negativo, la distancia también será negativa:
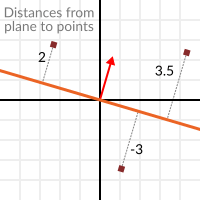
Esto nos permite saber de qué lado del plano está un punto.
Alejado del origen¶
¡Sé lo que estás pensando! Hasta ahora esto es agradable, pero los planos reales están por todas partes en el espacio, no sólo pasando a través del origen. Quieres acción en un plano real y la quieres ahora.
Recuerda que los planos no sólo dividen el espacio en dos, sino que también tienen polaridad. Esto significa que es posible tener planos perfectamente superpuestos, pero sus polos negativos y positivos están intercambiados.
Con esto en mente, describamos un plano completo como un normal N y una distancia desde el origen escalar D. Así, nuestro plano está representado por N y D. Por ejemplo:
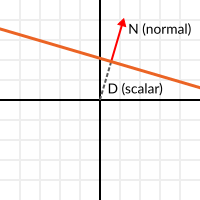
Para matemáticas 3D, Godot proporciona un tipo integrado Plano que maneja esto.
Básicamente, N y D pueden representar cualquier plano en el espacio, ya sea para 2D o 3D (dependiendo de la cantidad de dimensiones de N) y la matemática es la misma para ambos. Es igual que antes, pero D es la distancia desde el origen hasta el plano, viajando en dirección N. Por ejemplo, imagina que quieres llegar a un punto en el plano, simplemente lo harás:
var point_in_plane = N*D
var pointInPlane = N * D;
Esto estirará (redimensionará) el vector normal y lo hará tocar el plano. Esta matemática puede parecer confusa, pero en realidad es mucho más simple de lo que parece. Si queremos decir, de nuevo, la distancia desde el punto al plano, hacemos lo mismo pero ajustando la distancia:
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
Lo mismo, usando una función integrada:
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
Esto, de nuevo, devolverá una distancia positiva o negativa.
Invertir la polaridad del plano se puede hacer negando tanto N como D. Esto dará como resultado un plano en la misma posición, pero con semiespacios negativos y positivos invertidos:
N = -N
D = -D
N = -N;
D = -D;
Godot also implements this operator in Plane. So, using the format below will work as expected:
var inverted_plane = -plane
var invertedPlane = -plane;
So, remember, the plane's main practical use is that we can calculate the distance to it. So, when is it useful to calculate the distance from a point to a plane? Let's see some examples.
Construyendo un plano en 2D¶
Los planos claramente no salen de la nada, así que deben ser construidos. Construirlos en 2D es fácil, esto se puede hacer desde un vector normal (vector unitario) y un punto, o desde dos puntos en el espacio.
In the case of a normal and a point, most of the work is done, as the normal is already computed, so calculate D from the dot product of the normal and the point.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
Para dos puntos en el espacio, en realidad hay dos planos que pasan a través de ellos, compartiendo el mismo espacio pero con el normal apuntando a las direcciones opuestas. Para calcular la normal a partir de los dos puntos, primero se debe obtener el vector de dirección, y luego se debe girar 90° a cada lado:
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
The rest is the same as the previous example. Either point_a or point_b will work, as they are in the same plane:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Doing the same in 3D is a little more complex and is explained further down.
Algunos ejemplos de planos¶
Here is an example of what planes are useful for. Imagine you have a convex polygon. For example, a rectangle, a trapezoid, a triangle, or just any polygon where no faces bend inwards.
Para cada segmento del polígono, calculamos el plano que pasa por ese segmento. Una vez que tenemos la lista de planos, podemos hacer las cosas de forma ordenada, por ejemplo comprobar si un punto está dentro del polígono.
Pasamos por todos los planos, si podemos encontrar un plano donde la distancia al punto es positiva, entonces el punto está fuera del polígono. Si no podemos, entonces el punto está dentro.
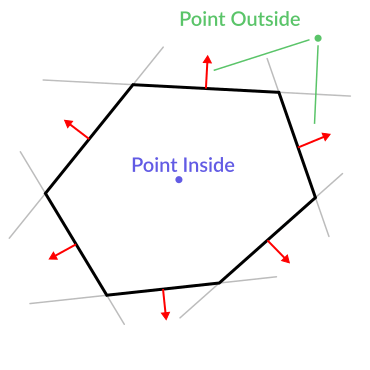
El código debería ser algo así:
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
Bastante genial ¿verdad? ¡Pero esto se pone mucho mejor! Con un poco más de esfuerzo, una lógica similar nos hará saber cuando dos polígonos convexos se superponen también. Esto se llama Teorema del Eje Separador (o SAT) y la mayoría de los motores de física lo utilizan para detectar colisiones.
Con un punto, basta con comprobar si un plano devuelve una distancia positiva para saber si el punto está fuera. Con otro polígono, debemos encontrar un plano donde todos los demás puntos del polígono devuelvan una distancia positiva al mismo. Esta comprobación se realiza con los planos de A contra los puntos de B, y luego con los planos de B contra los puntos de A:
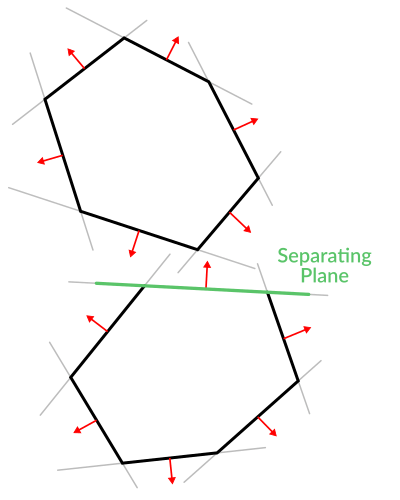
El código debería ser algo así:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Como pueden ver, los planos son muy útiles, y esta es la punta del iceberg. Te estarás preguntando qué pasa con los polígonos no convexos. Esto es usualmente manejado dividiendo el polígono cóncavo en polígonos convexos más pequeños, o usando una técnica como BSP (la cual no se usa mucho hoy en día).
Detección de colisiones en 3D¶
Esta es otra píldora de información, una recompensa por ser paciente y seguir el ritmo de este largo tutorial. Aquí hay otro pedazo de sabiduría. Esto podría no ser algo con un caso de uso directo (Godot ya hace detección de colisiones bastante bien) pero es usado por casi todos los motores de física y librerías de detección de colisiones :)
¿Recuerdas que convertir una forma convexa en 2D en un array de planos 2D era útil para la detección de colisiones? Podrías detectar si un punto estaba dentro de cualquier forma convexa, o si dos formas convexas 2D se solapaban.
Bueno, esto también funciona en 3D, si dos formas poliédricas 3D chocan, no podrás encontrar un plano de separación. Si se encuentra un plano de separación, entonces las formas definitivamente no están colisionando.
Para refrescar un poco un plano de separación significa que todos los vértices del polígono A están en un lado del plano, y todos los vértices del polígono B están en el otro lado. Este plano es siempre uno de los planos frontales del polígono A o del polígono B.
En 3D, sin embargo, hay un problema con este enfoque, porque es posible que, en algunos casos, no se pueda encontrar un plano de separación. Este es un ejemplo de tal situación:

Para evitarlo, algunos planos adicionales necesitan ser evaluados como separadores, estos planos son el producto vectorial entre los bordes del polígono A y los bordes del polígono B
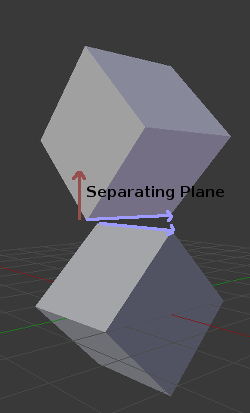
Así que el algoritmo final es algo así como:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Más información¶
Para más información sobre el uso de la matemática vectorial en Godot, consulta el siguiente artículo:
Si desea una explicación adicional, debería ver la excelente serie de videos de 3Blue1Brown "Essence of Linear Algebra": https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab