Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Beziers, Kurven und Pfade¶
Bezierkurven sind eine mathematische Annäherung an natürliche geometrische Formen. Wir verwenden sie, um eine Kurve mit möglichst wenig Informationen und einem hohen Maß an Flexibilität darzustellen.
Im Gegensatz zu abstrakteren mathematischen Konzepten wurden Bezier-Kurven für das Industriedesign entworfen. Sie sind ein beliebtes Werkzeug in der Grafiksoftwareindustrie.
Sie basieren auf interpolation die wir im vorherigen Artikel gesehen haben und kombinieren mehrere Schritte um glatte Kurven zu erstellen. Um besser zu verstehen wie Bezier-Kurven funktionieren, beginnen wir mit der einfachsten Form: Quadratisches Bezier.
Quadratisches Bezier¶
Nehmen Sie drei Punkte, das Minimum, das erforderlich ist, damit quadratisches Bezier funktioniert:
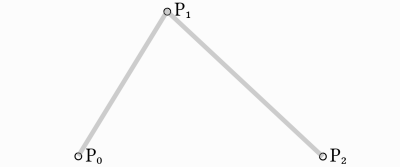
Um eine Kurve zwischen ihnen zu zeichnen, interpolieren wir zunächst allmählich über die beiden Vertices jedes der beiden Segmente, die durch die drei Punkte gebildet werden, und verwenden dabei Werte zwischen 0 und 1. Dadurch erhalten wir zwei Punkte, die sich entlang der Segmente bewegen, wenn wir den Wert von t ändern.
func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
}
Wir interpolieren dann q0 und q1, um einen einzelnen Punkt r zu erhalten, der sich entlang einer Kurve bewegt.
var r = q0.lerp(q1, t)
return r
Vector2 r = q0.Lerp(q1, t);
return r;
Diese Art wird als Quadratische Bezier-Kurve bezeichnet.
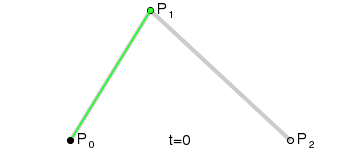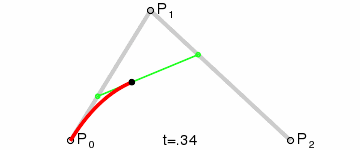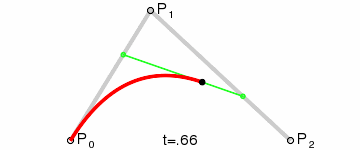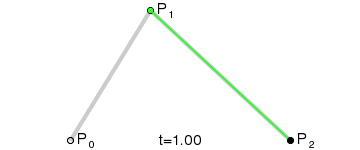
(Bildquelle: Wikipedia)
Kubisches Bezier¶
Aufbauend auf dem vorherigen Beispiel können wir mehr Kontrolle erhalten, indem wir zwischen vier Punkten interpolieren.
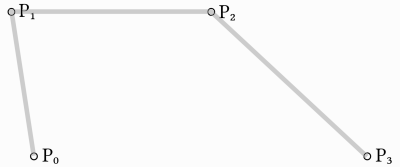
Wir verwenden zuerst eine Funktion mit vier Parametern, um vier Punkte als Eingabe zu verwenden: p0, p1, p2 und p3:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
}
Wir wenden eine lineare Interpolation auf jedes Paar von Punkten an, um sie auf drei zu reduzieren:
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Wir nehmen dann unsere drei Punkte und reduzieren sie auf zwei:
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
und auf einen:
var s = r0.lerp(r1, t)
return s
Vector2 s = r0.Lerp(r1, t);
return s;
Hier ist die komplette Funktion:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
var s = r0.lerp(r1, t)
return s
private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Vector2 s = r0.Lerp(r1, t);
return s;
}
Das Ergebnis ist eine glatte Kurve, die zwischen allen vier Punkten interpoliert:
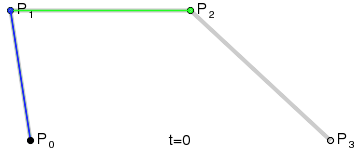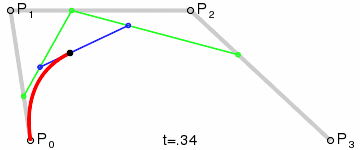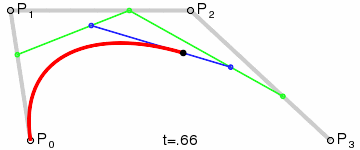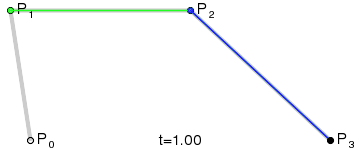
(Bildquelle: Wikipedia)
Bemerkung
Die kubische Bezier-Interpolation funktioniert in 3D genauso. Verwenden Sie einfach Vector3 anstelle von Vector2.
Kontrollpunkte hinzufügen¶
Aufbauend auf Kubischen Beziers können wir die Funktionsweise von zwei Punkten ändern, um die Form unserer Kurve frei zu kontrollieren. Anstatt p0, p1, p2 und p3 zu haben, speichern wir sie wie folgt:
point0 = p0: Ist der erste Punkt, die Quellecontrol0 = p1 - p0: Ist ein Vektor relativ zum ersten Kontrollpunktcontrol1 = p3 - p2: Ist ein Vektor relativ zum zweiten Kontrollpunktpoint1 = p3: Ist der zweite Punkt, das Ziel
Auf diese Weise haben wir zwei Punkte und zwei Kontrollpunkte, die relative Vektoren zu den jeweiligen Punkten sind. Wenn Sie zuvor Grafik- oder Animationssoftware verwendet haben, kommt Ihnen dies möglicherweise bekannt vor:
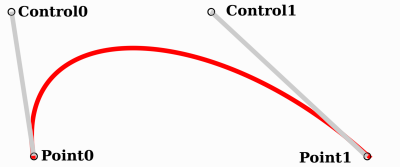
So werden Bezier-Kurven in Grafikprogrammen dargestellt, und so funktionieren und sehen sie in Godot aus.
Curve2D, Curve3D, Path und Path2D¶
Es gibt zwei Objekte, die Kurven enthalten: Curve3D und Curve2D (für 3D bzw. 2D).
Sie können mehrere Punkte enthalten, wodurch längere Pfade möglich sind. Es ist auch möglich, sie auf Nodes zu setzen: Path3D und Path2D (auch für 3D bzw. 2D):
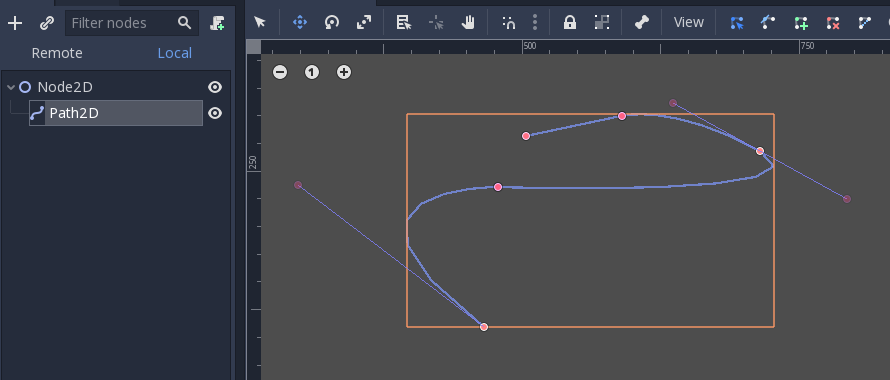
Ihre Verwendung ist jedoch möglicherweise nicht ganz offensichtlich. Im Folgenden werden die häufigsten Anwendungsfälle für Bezier-Kurven beschrieben.
Auswerten¶
Sie nur auszuwerten, kann eine Option sein, ist aber in den meisten Fällen nicht sehr nützlich. Der große Nachteil von Bezier-Kurven ist, dass, wenn man sie mit konstanter Geschwindigkeit durchläuft, von t = 0 bis t = 1, die eigentliche Interpolation nicht mit konstanter Geschwindigkeit erfolgt. Die Geschwindigkeit ist auch eine Interpolation zwischen den Abständen zwischen den Punkten p0, p1, p2 und p3 und es gibt keinen mathematisch einfachen Weg, die Kurve mit konstanter Geschwindigkeit zu durchlaufen.
Lassen Sie uns ein Beispiel mit dem folgenden Pseudocode durchspielen:
var t = 0.0
func _process(delta):
t += delta
position = _cubic_bezier(p0, p1, p2, p3, t)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = CubicBezier(p0, p1, p2, p3, _t);
}

Wie Sie sehen können, variiert die Geschwindigkeit (in Pixel pro Sekunde) des Kreises, obwohl t mit konstanter Geschwindigkeit erhöht wird. Dies macht es schwierig, Beziers ohne Weiteres in der Praxis zu verwenden.
Zeichnen¶
Das Zeichnen von Beziers (oder Objekten basierend auf der Kurve) ist ein sehr häufiger Anwendungsfall, aber auch nicht einfach. In fast jedem Fall müssen Bezier-Kurven in eine Menge von Segmenten konvertiert werden. Dies ist jedoch normalerweise schwierig, ohne eine sehr große Menge davon zu erzeugen.
Der Grund dafür ist, dass einige Abschnitte einer Kurve (insbesondere Ecken) möglicherweise eine beträchtliche Anzahl von Punkten erfordern, andere Abschnitte möglicherweise nicht:

Wenn beide Kontrollpunkte 0, 0 wären (denken Sie daran, dass es sich um relative Vektoren handelt), wäre die Bezier-Kurve nur eine gerade Linie (daher wäre das Zeichnen einer großen Anzahl von Punkten verschwenderisch).
Bevor Bezier-Kurven gezeichnet werden können, ist eine Tesselierung erforderlich. Dies geschieht häufig mit einer rekursiven Funktion oder einer Divide-and-Conquer-Funktion, die eine Kurve so lange aufteilt, bis der Krümmungsbetrag unter einen bestimmten Schwellenwert fällt.
Die Curve-Klassen bieten dies über die Funktion Curve2D.tessellate() (die optionale Stufen der Rekursion und Winkel Toleranz-Argumente annimmt). Auf diese Weise ist es einfacher etwas basierend auf einer Kurve zu zeichnen.
Durchlaufen¶
Der letzte häufige Anwendungsfall für die Kurven besteht darin, sie zu durchlaufen. Aufgrund der zuvor erwähnten konstanten Geschwindigkeit ist dies ebenfalls schwierig.
Um dies zu erleichtern, müssen die Kurven in äquidistante Punkte gebacken werden. Auf diese Weise können sie mit regulärer Interpolation (die mit einer kubischen Option weiter verbessert werden kann) angenähert werden. Um dies zu tun, verwenden Sie einfach die Methode Curve3D.sample_baked() zusammen mit Curve2D.get_baked_length(). Der erste Aufruf einer dieser Methoden wird die Kurve intern backen.
Das Durchlaufen mit konstanter Geschwindigkeit kann also mit folgendem Pseudocode durchgeführt werden:
var t = 0.0
func _process(delta):
t += delta
position = curve.sample_baked(t * curve.get_baked_length(), true)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}
Und das Ergebnis ist dann eine Bewegung mit konstanter Geschwindigkeit:
