Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Matrizen und Transformationen¶
Einführung¶
Bevor Sie dieses Tutorial lesen, empfehlen wir das Vektormathematik-Tutorial sorgfältig lesen und verstehen, da dieses Tutorial Kenntnisse über Vektoren voraussetzt.
In diesem Tutorial geht es um Transformationen und wie wir sie in Godot mithilfe von Matrizen darstellen. Es ist keine ausführliche Anleitung zu Matrizen. Transformationen werden meistens als Translation, Rotation und Skalierung angewendet, daher konzentrieren wir uns darauf, wie diese mit Matrizen dargestellt werden.
Der größte Teil dieser Anleitung konzentriert sich auf 2D und verwendet Transform2D und Vector2, aber die Funktionsweise in 3D ist sehr ähnlich.
Bemerkung
Wie im vorherigen Tutorial erwähnt, ist es wichtig, sich daran zu erinnern, dass in Godot die Y-Achse in 2D nach unten zeigt. Dies ist das Gegenteil davon, wie die meisten Schulen lineare Algebra unterrichten, wo die Y-Achse nach oben zeigt.
Bemerkung
Die Konvention ist, dass die X-Achse rot ist, die Y-Achse grün und die Z-Achse blau. Dieses Tutorial ist farbcodiert, um diesen Konventionen zu entsprechen. Wir werden jedoch auch den Ursprungsvektor mit einer blauen Farbe darstellen.
Matrixkomponenten und die Einheitsmatrix¶
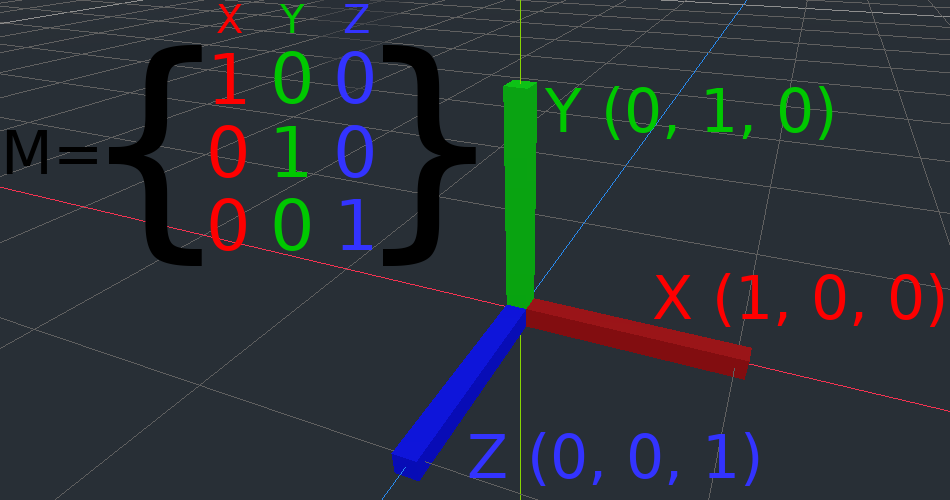
Die Einheitsmatrix repräsentiert eine Transformation ohne Translation, ohne Rotation und ohne Skalierung. Betrachten wir zunächst die Einheitsmatrix und ihre Beziehung zu ihrer visuellen Darstellung.
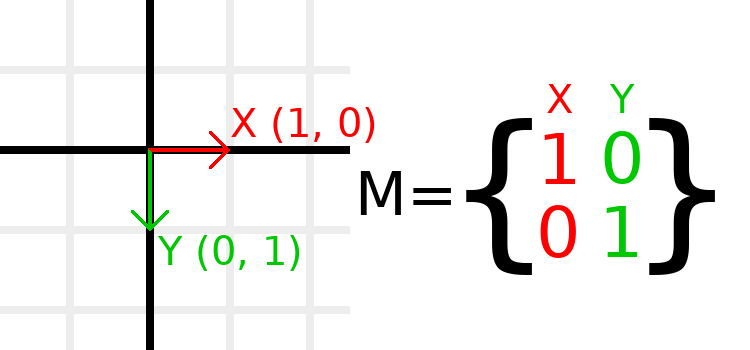
Matrizen haben Zeilen und Spalten, und eine Transformationsmatrix hat spezifische Konventionen, wofür jede zuständig ist.
Im obigen Bild sehen wir, dass der rote X-Vektor durch die erste Spalte der Matrix dargestellt wird und der grüne Y-Vektor entsprechend durch die zweite Spalte dargestellt wird. Durch eine Änderung der Spalten werden diese Vektoren geändert. Wir werden in den nächsten Beispielen sehen, wie sie manipuliert werden können.
Sie sollten sich keine Gedanken über die direkte Bearbeitung von Zeilen machen, da wir normalerweise mit Spalten arbeiten. Sie können sich jedoch vorstellen, dass die Zeilen der Matrix angeben, welche Vektoren zur Bewegung in eine bestimmte Richtung beitragen.
Wenn wir uns auf einen Wert wie t.x.y beziehen, ist das die Y-Komponente des X-Spaltenvektors. Mit anderen Worten, die untere linke Seite der Matrix. In ähnlicher Weise steht t.x.x für oben links, t.y.x für oben rechts und t.y.y für unten rechts, wobei t das Transform2D ist.
Skalierung der Transformationsmatrix¶
Das Anwenden einer Skalierung ist eine der am einfachsten zu verstehenden Operationen. Beginnen wir damit, das Godot-Logo unter unsere Vektoren zu legen, damit wir die Auswirkungen auf ein Objekt visuell sehen können:
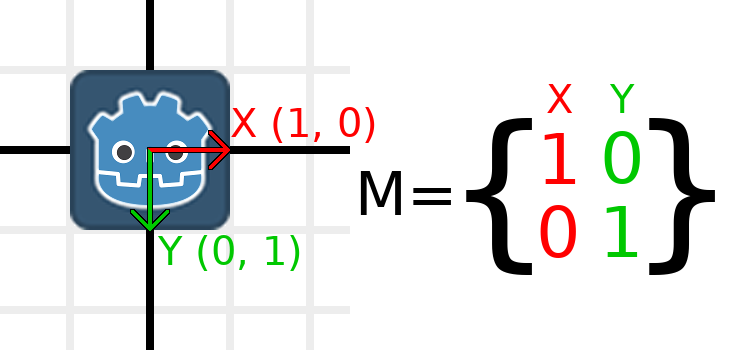
Um die Matrix zu skalieren, müssen wir nur jede Komponente mit der gewünschten Skalierung multiplizieren. Skalieren wir sie mit 2. 1 mal 2 wird zu 2, und 0 mal 2 wird zu 0, so dass wir am Ende Folgendes erhalten:
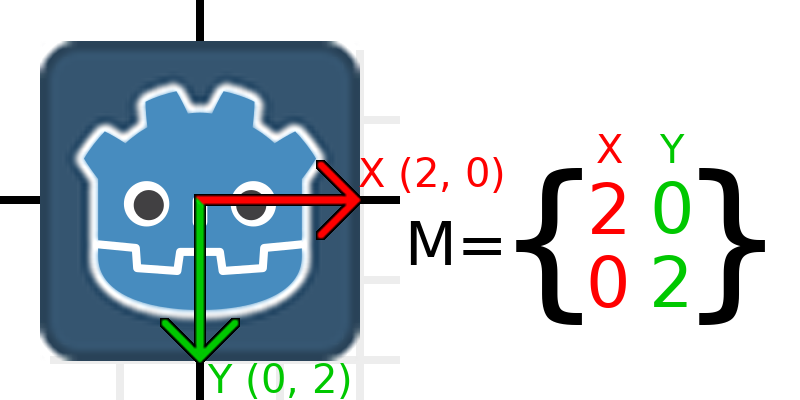
Um dies im Code zu tun, multiplizieren wir jeden der Vektoren:
var t = Transform2D()
# Scale
t.x *= 2
t.y *= 2
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Scale
t.X *= 2;
t.Y *= 2;
Transform = t; // Change the node's transform to what we calculated.
Wenn wir den ursprünglichen Maßstab wiederherstellen wollen, können wir jede Komponente mit 0.5 multiplizieren. Das ist so ziemlich alles, was es zum Skalieren einer Transformationsmatrix braucht.
Um die Skalierung des Objekts aus einer bestehenden Transformationsmatrix zu berechnen, können Sie length() auf jeden der Spaltenvektoren anwenden.
Bemerkung
In echten Projekten können Sie die Methode scaled() verwenden, um eine Skalierung durchzuführen.
Rotation der Transformationsmatrix¶
Wir beginnen auf die gleiche Weise wie zuvor, mit dem Godot-Logo unter der Einheitsmatrix:

Nehmen wir als Beispiel an, wir wollen unser Godot-Logo um 90 Grad im Uhrzeigersinn rotieren. Im Moment zeigt die X-Achse nach rechts und die Y-Achse nach unten. Wenn wir diese in unserem Kopf rotieren, würden wir logischerweise sehen, dass die neue X-Achse nach unten und die neue Y-Achse nach links zeigen sollte.
Sie können sich vorstellen, dass Sie sowohl das Godot-Logo als auch seine Vektoren nehmen und es dann um den Mittelpunkt drehen. Je nachdem, wo man die Drehung beendet, bestimmt die Ausrichtung der Vektoren das Aussehen der Matrix.
Wir müssen "unten" und "links" in Normalen-Koordinaten darstellen, d.h. wir setzen X auf (0, 1) und Y auf (-1, 0). Dies sind auch die Werte von Vector2.DOWN und Vector2.LEFT. Wenn wir dies tun, erhalten wir das gewünschte Ergebnis der Rotation des Objekts:
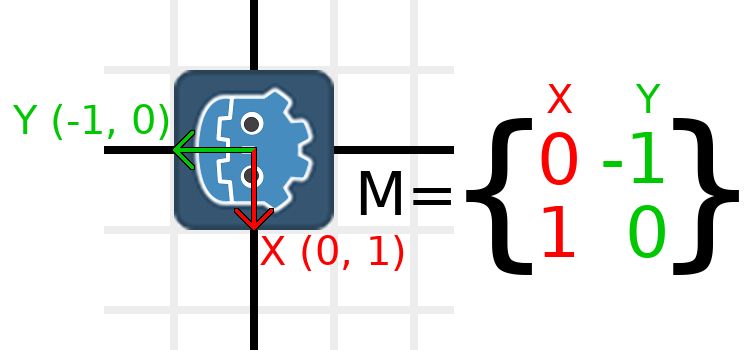
Wenn Sie Schwierigkeiten haben, das oben Beschriebene zu verstehen, versuchen Sie diese Übung: Schneiden Sie ein Quadrat aus Papier aus, zeichnen Sie X- und Y-Vektoren darauf, legen Sie es auf Millimeterpapier, rotieren Sie es und notieren Sie die Endpunkte.
Um eine Rotation im Code durchzuführen, müssen wir in der Lage sein, die Werte programmatisch zu berechnen. Dieses Bild zeigt die Formeln, die zur Berechnung der Transformationsmatrix aus einem Rotationswinkel erforderlich sind. Keine Sorge, wenn dieser Teil kompliziert erscheint: Ich verspreche, dass es das Schwierigste ist, was Sie wissen müssen.
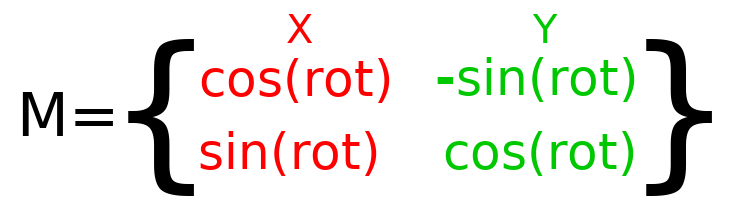
Bemerkung
Godot stellt alle Drehungen im Bogenmaß und nicht in Grad dar. Eine volle Drehung ist TAU oder PI*2 Bogenmaß, und eine Vierteldrehung von 90 Grad ist TAU/4 oder PI/2 Bogenmaß. Die Arbeit mit TAU führt in der Regel zu einem besser lesbaren Code.
Bemerkung
Interessante Fakt am Rande: In Godot ist Y nicht nur unten, sondern Rotation wird auch im Uhrzeigersinn dargestellt. Das bedeutet, dass sich alle mathematischen und trigonometrischen Funktionen genauso verhalten wie in einem System mit Y nach oben und gegen den Uhrzeigersinn, da sich diese Unterschiede "aufheben". Sie können sich Rotationen in beiden Systemen als "von X nach Y" vorstellen.
Um eine Drehung von 0.5 Bogenmaß (ca. 28.65 Grad) durchzuführen, setzen wir einen Wert von 0.5 in die obige Formel ein und werten aus, was die tatsächlichen Werte sein sollten:
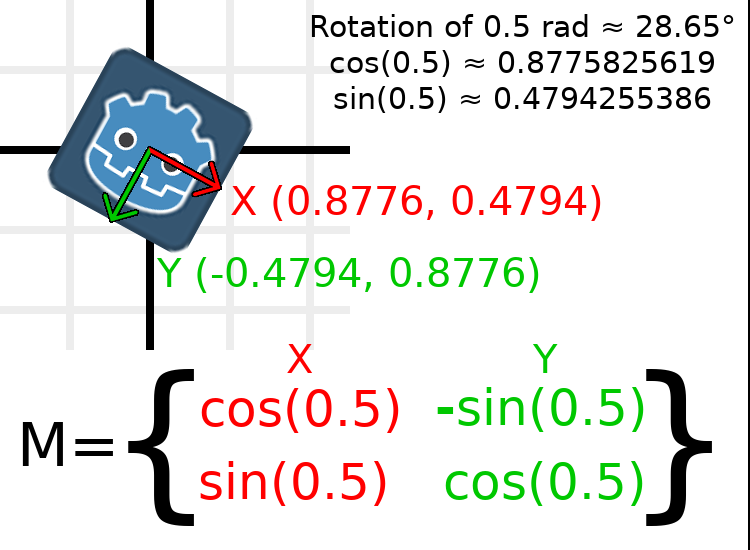
So würde das im Code gemacht werden (hängen Sie das Skript an einen Node2D):
var rot = 0.5 # The rotation to apply.
var t = Transform2D()
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
transform = t # Change the node's transform to what we calculated.
float rot = 0.5f; // The rotation to apply.
Transform2D t = Transform2D.Identity;
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
Transform = t; // Change the node's transform to what we calculated.
Um die Rotation des Objekts aus einer bestehenden Transformationsmatrix zu berechnen, können Sie atan2(t.x.y, t.x.x) verwenden, wobei t das Transform2D ist.
Bemerkung
In echten Projekten können Sie die Methode rotated() verwenden, um Rotationen durchzuführen.
Basis der Transformationsmatrix¶
Bisher haben wir nur mit den Vektoren x und y gearbeitet, die für die Darstellung von Rotation, Skalierung und/oder Scherung zuständig sind (fortgeschritten, wird am Ende behandelt). Die X- und Y-Vektoren werden zusammen als Basis der Transformationsmatrix bezeichnet. Die Begriffe "Basis" und "Basisvektoren" sind wichtig zu wissen.
Sie haben vielleicht bemerkt, dass Transform2D eigentlich drei Vector2 Werte hat: x, y und origin. Der origin-Wert ist nicht Teil der Basis, aber er ist Teil der Transformation, und wir brauchen ihn, um die Position zu repräsentieren. Von nun an werden wir den Ursprungsvektor in allen Beispielen im Auge behalten. Man kann sich den Ursprung als eine weitere Spalte vorstellen, aber oft ist es besser, ihn als völlig eigenständig zu betrachten.
Beachten Sie, dass Godot in 3D eine separate Basis-Struktur für die drei Vector3-Werte der Basis hat, da der Code komplex werden kann und es sinnvoll ist, ihn von Transform3D zu trennen (das aus einer Basis und einem zusätzlichen Vector3 für den Ursprung besteht).
Verschieben der Transformationsmatrix¶
Das Ändern des Ursprungsvektors wird als Translation der Transformationsmatrix bezeichnet. Translation ist im Grunde ein technischer Begriff für das "Verschieben" des Objekts, aber es beinhaltet ausdrücklich keine Drehung.
Lassen Sie uns ein Beispiel durcharbeiten, um dies zu verstehen. Wir werden wie beim letzten Mal mit der Einheitstransformation beginnen, außer dass wir diesmal den Ursprungsvektor beobachten.
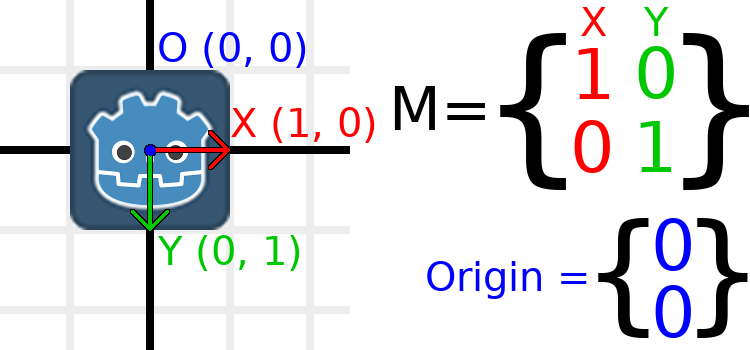
Wenn wir das Objekt an eine Position von (1, 2) verschieben wollen, müssen wir seinen Ursprungsvektor auf (1, 2) setzen:
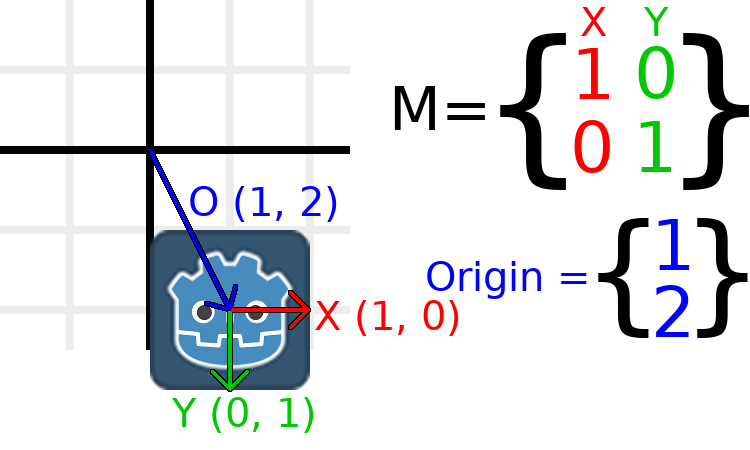
Es gibt auch eine Methode translated(), die eine andere Operation durchführt als das direkte Hinzufügen oder Ändern von origin. Die Methode translated() übersetzt das Objekt relativ zu seiner eigenen Drehung. Zum Beispiel wird ein um 90 Grad im Uhrzeigersinn gedrehtes Objekt nach rechts verschoben, wenn translated() mit Vector2.UP durchgeführt wird.
Bemerkung
Das 2D-System von Godot verwendet Koordinaten auf der Basis von Pixeln, so dass Sie in tatsächlichen Projekten um Hunderte von Einheiten verschieben werden.
Fügen wir alles zusammen¶
Jetzt werden wir alles, was wir bisher erwähnt haben, auf eine Transformation anwenden. Erstellen Sie dazu ein Projekt mit einem Sprite2D-Node und verwenden Sie das Godot-Logo als Texturressource.
Setzen wir die Translation auf (350, 150), rotieren wir um -0.5 Bogenmaß und skalieren wir um 3. Ich habe einen Screenshot und den Code zur Reproduktion gepostet, aber ich möchte Sie ermutigen, den Screenshot zu reproduzieren, ohne sich den Code anzusehen!
var t = Transform2D()
# Translation
t.origin = Vector2(350, 150)
# Rotation
var rot = -0.5 # The rotation to apply.
t.x.x = cos(rot)
t.y.y = cos(rot)
t.x.y = sin(rot)
t.y.x = -sin(rot)
# Scale
t.x *= 3
t.y *= 3
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Translation
t.Origin = new Vector2(350, 150);
// Rotation
float rot = -0.5f; // The rotation to apply.
t.X.X = t.Y.Y = Mathf.Cos(rot);
t.X.Y = t.Y.X = Mathf.Sin(rot);
t.Y.X *= -1;
// Scale
t.X *= 3;
t.Y *= 3;
Transform = t; // Change the node's transform to what we calculated.
Scheren der Transformationsmatrix (fortgeschritten)¶
Bemerkung
Wenn Sie nur wissen wollen, wie man Transformationsmatrizen verwendet, können Sie diesen Abschnitt des Tutorials getrost überspringen. In diesem Abschnitt wird ein selten genutzter Aspekt von Transformationsmatrizen untersucht, um ein Verständnis für sie zu entwickeln.
Node2D bietet von Haus aus eine Scher-Eigenschaft.
Sie haben vielleicht bemerkt, dass eine Transformation mehr Freiheitsgrade hat als die Kombination der oben genannten Aktionen. Die Basis einer 2D-Transformationsmatrix hat insgesamt vier Zahlen in zwei Vector2-Werten, während ein Rotationswert und ein Vector2 für die Skalierung nur 3 Zahlen haben. Das übergeordnete Konzept für den fehlenden Freiheitsgrad wird Scheren genannt.
Normalerweise stehen die Basisvektoren immer senkrecht aufeinander. Die Scherung kann jedoch in einigen Situationen nützlich sein, und das Verständnis der Scherung hilft Ihnen zu verstehen, wie Transformationen funktionieren.
Um Ihnen visuell zu zeigen, wie es aussehen wird, überlagern wir das Godot-Logo mit einem Raster:
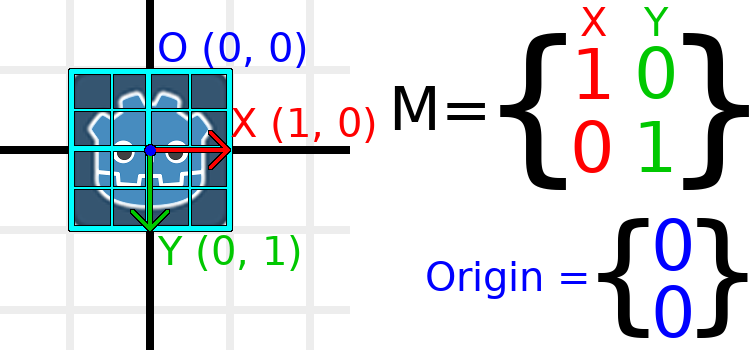
Jeder Punkt auf diesem Raster ergibt sich aus der Addition der Basisvektoren. Die rechte untere Ecke ist X + Y, während die rechte obere Ecke X - Y ist. Wenn wir die Basisvektoren ändern, bewegt sich das gesamte Raster mit, da das Raster aus den Basisvektoren zusammengesetzt ist. Alle Linien des Rasters, die derzeit parallel sind, bleiben parallel, egal welche Änderungen wir an den Basisvektoren vornehmen.
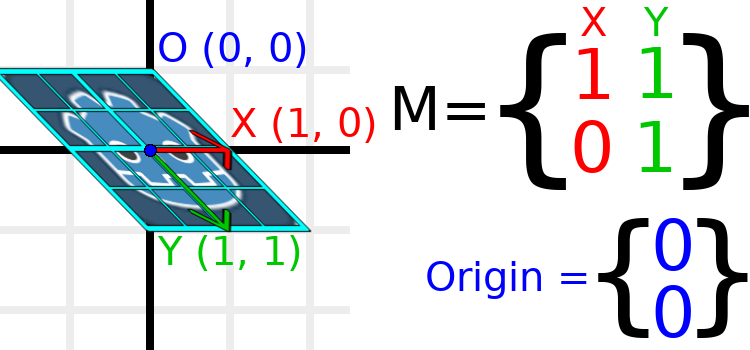
Als Beispiel setzen wir Y auf (1, 1):
var t = Transform2D()
# Shear by setting Y to (1, 1)
t.y = Vector2.ONE
transform = t # Change the node's transform to what we calculated.
Transform2D t = Transform2D.Identity;
// Shear by setting Y to (1, 1)
t.Y = Vector2.One;
Transform = t; // Change the node's transform to what we calculated.
Bemerkung
Sie können die Rohwerte eines Transform2D im Editor nicht einstellen, also müssen Sie Code verwenden, wenn Sie das Objekt scheren wollen.
Da die Vektoren nicht mehr senkrecht zueinander stehen, ist das Objekt geschert worden. Der untere Mittelpunkt des Rasters, der relativ zu sich selbst (0, 1) ist, befindet sich jetzt an der Weltposition (1, 1).
Die Intra-Objekt-Koordinaten werden in Texturen als UV-Koordinaten bezeichnet, so dass wir diese Terminologie hier übernehmen wollen. Um die Weltposition von einer relativen Position aus zu bestimmen, lautet die Formel U * X + V * Y, wobei U und V Zahlen und X und Y die Basisvektoren sind.
Die untere rechte Ecke des Gitters, die sich immer an der UV-Position (1, 1) befindet, befindet sich an der Weltposition (2, 1), die sich aus X*1 + Y*1, also (1, 0) + (1, 1) oder (1 + 1, 0 + 1) oder (2, 1) ergibt. Dies stimmt mit unserer Beobachtung überein, wo sich die untere rechte Ecke des Bildes befindet.
Ebenso befindet sich die rechte obere Ecke des Gitters, die sich immer an der UV-Position (1, -1) befindet, an der Weltposition (0, -1), die sich aus X*1 + Y*-1 errechnet, was (1, 0) - (1, 1) oder (1 - 1, 0 - 1) oder (0, -1) ist. Dies stimmt mit unserer Beobachtung überein, wo sich die rechte obere Ecke des Bildes befindet.
Sie verstehen nun hoffentlich, wie sich eine Transformationsmatrix auf das Objekt auswirkt und welche Beziehung zwischen den Basisvektoren und der Änderung der Weltposition der "UV"- oder "Intra-Koordinaten" des Objekts besteht.
Bemerkung
In Godot werden alle Transformationsberechnungen relativ zum übergeordneten Node durchgeführt. Wenn wir uns auf die "Weltposition" beziehen, wäre das relativ zum übergeordneten Node, wenn der Node einen übergeordneten Node hätte.
Wenn Sie weitere Erklärungen wünschen, sollten Sie sich das exzellente Video von 3Blue1Brown über lineare Transformationen ansehen: https://www.youtube.com/watch?v=kYB8IZa5AuE
Praktische Anwendungen von Transformationen¶
In tatsächlichen Projekten werden Sie normalerweise mit Transformationen innerhalb von Transformationen arbeiten, indem Sie mehrere Node2D oder Node3D-Nodes haben, die einander übergeordnet sind.
Es ist jedoch nützlich zu wissen, wie man die benötigten Werte manuell berechnen kann. Wir gehen darauf ein, wie Sie Transform2D oder Transform3D verwenden können, um Transformationen von Nodes manuell zu berechnen.
Positionen zwischen Transformationen konvertieren¶
Es gibt viele Fälle, in denen man eine Position in und aus einer Transformation konvertieren möchte. Zum Beispiel, wenn man eine Position relativ zum Spieler hat und die Weltposition (relativ zum Parent) finden möchte, oder wenn man eine Weltposition hat und wissen möchte, wo sie relativ zum Spieler ist.
Wir können herausfinden, wie ein Vektor relativ zum Spieler im World-Space definiert wäre, indem wir den Operator * verwenden:
# World space vector 100 units below the player.
print(transform * Vector2(0, 100))
// World space vector 100 units below the player.
GD.Print(Transform * new Vector2(0, 100));
Und wir können den Operator * in umgekehrter Reihenfolge verwenden, um eine Position im World-Space zu finden, die relativ zum Spieler definiert wäre:
# Where is (0, 100) relative to the player?
print(Vector2(0, 100) * transform)
// Where is (0, 100) relative to the player?
GD.Print(new Vector2(0, 100) * Transform);
Bemerkung
Wenn Sie im Voraus wissen, dass die Transformation auf (0, 0) positioniert ist, können Sie stattdessen die Methoden "basis_xform" oder "basis_xform_inv" verwenden, um die Translation überspringen.
Verschieben eines Objekts relativ zu sich selbst¶
Vor allem in 3D-Spielen ist es üblich, ein Objekt relativ zu sich selbst zu bewegen. In Ego-Shooter-Spielen möchte man zum Beispiel, dass sich die Figur nach vorne bewegt (-Z-Achse), wenn man W drückt.
Da die Basisvektoren die Orientierung relativ zum übergeordneten Objekt und der Ursprungsvektor die Position relativ zum übergeordneten Objekt darstellen, können wir ein Vielfaches der Basisvektoren addieren, um ein Objekt relativ zu sich selbst zu bewegen.
Dieser Code verschiebt ein Objekt um 100 Einheiten nach rechts:
transform.origin += transform.x * 100
Transform2D t = Transform;
t.Origin += t.X * 100;
Transform = t;
Um sich in 3D zu bewegen, müssten Sie "x" durch "basis.x" ersetzen.
Bemerkung
In tatsächlichen Projekten können Sie translate_object_local in 3D oder move_local_x und move_local_y in 2D verwenden, um dies zu tun.
Anwenden von Transformationen auf Transformationen¶
Eines der wichtigsten Dinge, die Sie über Transformationen wissen sollten ist, wie Sie mehrere davon zusammen verwenden können. Die Transformation eines übergeordneten Nodes wirkt sich auf alle untergeordneten Nodes aus. Lassen Sie uns ein Beispiel analysieren.
In diesem Bild hat der Child-Node eine "2" hinter den Komponentennamen, um sie vom Parent-Node zu unterscheiden. Bei so vielen Zahlen mag es etwas überwältigend aussehen, aber bedenken Sie, dass jede Zahl zweimal angezeigt wird (neben den Pfeilen und auch in den Matrizen) und dass fast die Hälfte der Zahlen Null ist.
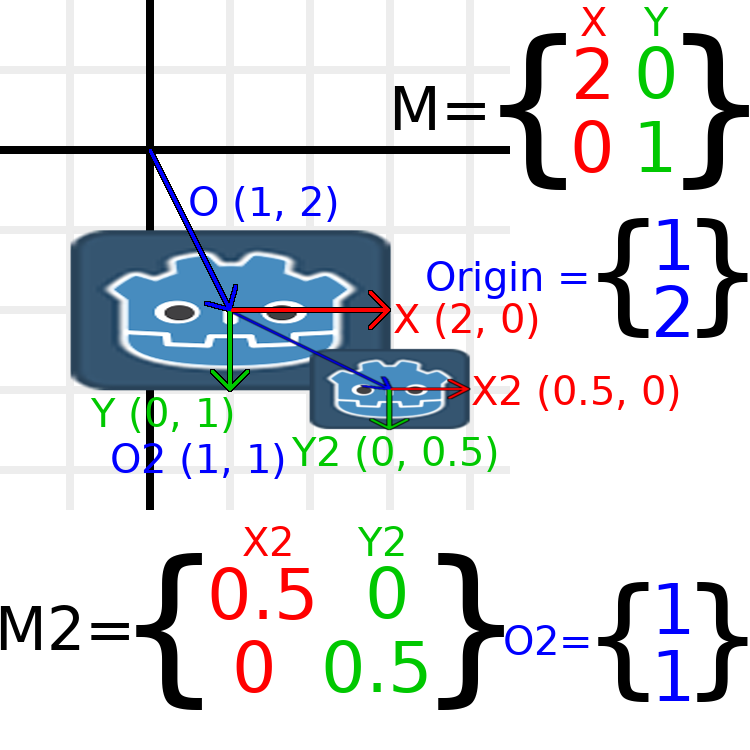
Die einzigen Transformationen, die hier stattfinden, sind, dass dem Parent-Node eine Skalierung von (2, 1), dem Child-Node ein Maßstab von (0.5, 0.5) und beiden Nodes eine Position zugewiesen wurde.
Alle Child-Transformationen werden von den Parent-Transformationen beeinflusst. Das Child hat eine Skalierung von (0.5, 0.5), so dass man erwarten würde, dass es ein Quadrat im Verhältnis 1:1 ist, und das ist es auch, aber nur relativ zum Parent. Der X-Vektor des Child liegt im World-Space bei (1, 0), weil er durch die Basisvektoren des Parent-Nodes skaliert wird. In ähnlicher Weise wird der Ursprungsvektor des Child-Nodes auf (1, 1) gesetzt, aber dadurch wird er im World-Space aufgrund der Basisvektoren des Parent Nodes auf (2, 1) verschoben.
Um die World-Space-Transformation der Child-Transformation manuell zu berechnen, würden wir den folgenden Code verwenden:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Calculate the child's world space transform
# origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
var origin = parent.x * child.origin.x + parent.y * child.origin.y + parent.origin
# basis_x = (2, 0) * 0.5 + (0, 1) * 0
var basis_x = parent.x * child.x.x + parent.y * child.x.y
# basis_y = (2, 0) * 0 + (0, 1) * 0.5
var basis_y = parent.x * child.y.x + parent.y * child.y.y
# Change the node's transform to what we calculated.
transform = Transform2D(basis_x, basis_y, origin)
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Calculate the child's world space transform
// origin = (2, 0) * 100 + (0, 1) * 100 + (100, 200)
Vector2 origin = parent.X * child.Origin.X + parent.Y * child.Origin.Y + parent.Origin;
// basisX = (2, 0) * 0.5 + (0, 1) * 0 = (0.5, 0)
Vector2 basisX = parent.X * child.X.X + parent.Y * child.X.Y;
// basisY = (2, 0) * 0 + (0, 1) * 0.5 = (0.5, 0)
Vector2 basisY = parent.X * child.Y.X + parent.Y * child.Y.Y;
// Change the node's transform to what we calculated.
Transform = new Transform2D(basisX, basisY, origin);
In tatsächlichen Projekten können wir die World-Space-Transformation des Child finden, indem wir eine Transformation auf eine andere mit dem Operator * anwenden:
# Set up transforms like in the image, except make positions be 100 times bigger.
var parent = Transform2D(Vector2(2, 0), Vector2(0, 1), Vector2(100, 200))
var child = Transform2D(Vector2(0.5, 0), Vector2(0, 0.5), Vector2(100, 100))
# Change the node's transform to what would be the child's world transform.
transform = parent * child
// Set up transforms like in the image, except make positions be 100 times bigger.
Transform2D parent = new Transform2D(2, 0, 0, 1, 100, 200);
Transform2D child = new Transform2D(0.5f, 0, 0, 0.5f, 100, 100);
// Change the node's transform to what would be the child's world transform.
Transform = parent * child;
Bemerkung
Beim Multiplizieren von Matrizen kommt es auf die Reihenfolge an! Verwechseln Sie sie nicht.
Zuletzt bewirkt die Anwendung der Einheitstransformation niemals etwas.
Wenn Sie weitere Erklärungen wünschen, sollten Sie sich das exzellente Video von 3Blue1Brown über die Zusammensetzung von Matrizen ansehen: https://www.youtube.com/watch?v=XkY2DOUCWMU
Invertieren einer Transformationsmatrix¶
Die Funktion "affine_inverse" gibt eine Transformation zurück, die eine vorherige Transformation "rückgängig macht". Dies kann in einigen Situationen nützlich sein. Schauen wir uns einige Beispiele an.
Das Multiplizieren einer inversen Transformation mit der normalen Transformation macht alle Transformationen rückgängig:
var ti = transform.affine_inverse()
var t = ti * transform
# The transform is the identity transform.
Transform2D ti = Transform.AffineInverse();
Transform2D t = ti * Transform;
// The transform is the identity transform.
Die Transformation einer Position durch eine Transformation und ihre Umkehrung ergibt dieselbe Position:
var ti = transform.affine_inverse()
position = transform * position
position = ti * position
# The position is the same as before.
Transform2D ti = Transform.AffineInverse();
Position = Transform * Position;
Position = ti * Position;
// The position is the same as before.
Wie funktioniert das alles in 3D?¶
Eine der großartigen Eigenschaften von Transformationsmatrizen ist, dass die 2D- und 3D-Transformationen sehr ähnlich funktionieren. Der gesamte Code und die Formeln, die oben für 2D verwendet wurden, funktionieren in 3D genauso, mit drei Ausnahmen: die Hinzufügung einer dritten Achse, dass jede Achse vom Typ Vector3 ist, und auch, dass Godot die Basis getrennt von der Transform3D speichert, da die Mathematik komplex werden kann und es sinnvoll ist, sie zu trennen.
Alle Konzepte für die Funktionsweise von Translation, Rotation, Skalierung und Scherung funktionieren in 3D genauso wie in 2D. Zum Skalieren nehmen wir jede Komponente und multiplizieren sie; zum Rotieren ändern wir, wohin jeder Basisvektor zeigt; zum Verschieben verändern wir den Ursprung; und zum Scheren ändern wir die Basisvektoren so, dass sie nicht senkrecht sind.
Wenn Sie möchten, ist es eine gute Idee, mit Transformationen herumzuspielen, um ein Verständnis dafür zu bekommen, wie sie funktionieren. Mit Godot können Sie 3D-Transformationsmatrizen direkt vom Inspektor aus bearbeiten. Sie können das folgende Projekt mit farbigen Linien und Würfeln herunterladen, um die Vektoren der Basis und den Ursprung sowohl in 2D als auch in 3D zu visualisieren: https://github.com/godotengine/godot-demo-projects/tree/master/misc/matrix_transform
Bemerkung
Sie können die Transformationsmatrix von Node2D nicht direkt im Inspektor von Godot 4.0 bearbeiten. Dies wird möglicherweise in einer zukünftigen Version von Godot geändert.
Wenn Sie zusätzliche Erklärungen wünschen, sollten Sie sich das exzellente Video von 3Blue1Brown über lineare 3D-Transformationen ansehen: https://www.youtube.com/watch?v=rHLEWRxRGiM
Darstellung der Rotation in 3D (fortgeschritten)¶
Der größte Unterschied zwischen 2D- und 3D-Transformationsmatrizen besteht darin, wie Sie die Rotation selbst ohne die Basisvektoren darstellen.
In 2D gibt es eine einfache Möglichkeit (atan2), zwischen einer Transformationsmatrix und einem Winkel zu wechseln. In 3D ist die Drehung zu komplex, um sie als eine Zahl darzustellen. Es gibt etwas, das Euler-Winkel genannt wird und Drehungen als eine Menge von 3 Zahlen darstellen kann, aber sie sind begrenzt und nicht sehr nützlich, außer für triviale Fälle.
In 3D verwenden wir normalerweise keine Winkel, sondern entweder eine Transformationsbasis (die in Godot so gut wie überall verwendet wird) oder Quaternionen. Godot kann Quaternionen mit der Struktur Quaternion darstellen. Ich schlage vor, dass Sie komplett ignorieren, wie sie im Detail funktionieren, da sie sehr kompliziert und unintuitiv sind.
Wenn Sie jedoch wirklich wissen müssen, wie es funktioniert, finden Sie hier einige großartige Ressourcen, die Sie durchgehen können:
https://www.youtube.com/watch?v=mvmuCPvRoWQ