Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Fortgeschrittene Vektormathematik¶
Flächen¶
Das Skalarprodukt hat eine weitere interessante Eigenschaft bei Einheitsvektoren. Stellen Sie sich vor, dass senkrecht zu diesem Vektor (und durch den Ursprung) eine Ebene verläuft. Ebenen teilen den gesamten Raum in positiv (über der Ebene) und negativ (unter der Ebene). Entgegen der landläufigen Meinung können Sie ihre Mathematik auch in 2D verwenden:
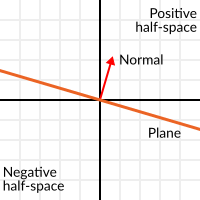
Einheitsvektoren, die senkrecht zu einer Oberfläche stehen (sie beschreiben also die Ausrichtung der Oberfläche), werden als Einheitsnormalenvektoren bezeichnet. Normalerweise werden sie jedoch nur als Normalen abgekürzt. Normalen erscheinen in Ebenen, 3D-Geometrie (um zu bestimmen, wo sich jede Fläche oder jeder Vertex befindet) usw. Eine Normale ist*ein **Einheitsvektor*, wird aber aufgrund seiner Verwendung Normale genannt. (Genau wie wir (0,0) den Ursprung nennen!).
Die Ebene geht durch den Ursprung und ihre Oberfläche steht senkrecht auf dem Einheitsvektor (oder Normalen). Die Seite, auf die der Vektor zeigt, ist der positive Halbraum, während die andere Seite der negative Halbraum ist. In 3D ist dies genau dasselbe, nur dass die Ebene eine unendliche Fläche ist und keine Linie (stellen Sie sich ein unendliches, flaches Blatt Papier vor, das Sie ausrichten können und das an den Ursprung geheftet ist).
Abstand zur Fläche¶
Nachdem klar ist, was eine Ebene ist, kehren wir zum Skalarprodukt zurück. Das Skalarprodukt zwischen einem Einheitsvektor und einem beliebigen Punkt im Raum (ja, diesmal machen wir ein Skalarprodukt zwischen Vektor und Position) gibt den Abstand vom Punkt zur Ebene zurück:
var distance = normal.dot(point)
var distance = normal.Dot(point);
Aber nicht nur die absolute Entfernung: wenn sich der Punkt im negativen Halbraum befindet, ist auch die Entfernung negativ:
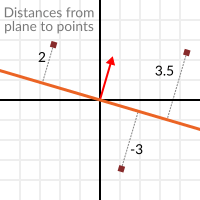
Dies erlaubt uns zu sagen, auf welcher Seite der Ebene ein Punkt sich befindet.
Wegbewegen vom Ursprung¶
Ich weiß was Sie denken! Schön und gut, aber echte Ebenen sind überall im Raum und durchqueren nicht unbedingt den Ursprung. Sie wollen echte Ebenen und Sie möchten sie jetzt.
Bedenken Sie, dass Ebenen nicht nur den Raum teilen, sie haben auch eine Polarität. Das bedeutet, es können zwei perfekt überlappende Ebenen vorhanden sein, aber deren positive und negative Halb-Räume sind vertauscht.
Mit diesem Wissen können wir nun eine komplette Ebene als normale N und eine Distanz vom Ursprung als Skalar D bezeichnen. Somit wird unsere Ebene mittels N und D repräsentiert, zum Beispiel:
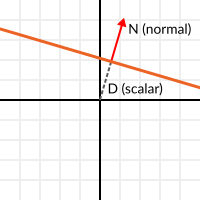
Für 3D-Mathematik bietet Godot einen Built-in-Typ Plane, der dies handhabt.
Grundsätzlich können N und D jede Ebene im Raum darstellen, sei es für 2D oder 3D (abhängig von der Anzahl der Dimensionen von N), und die Mathematik ist für beide gleich. Es ist das gleiche wie zuvor, aber D ist die Entfernung vom Ursprung zur Ebene in N-Richtung. Stellen Sie sich als Beispiel vor, Sie möchten einen Punkt in der Ebene erreichen. Sie tun einfach Folgendes:
var point_in_plane = N*D
var pointInPlane = N * D;
Dadurch wird der Normalenvektor gedehnt (seine Größe geändert) und er berührt die Ebene. Diese Mathematik mag verwirrend erscheinen, ist aber tatsächlich viel einfacher als es scheint. Wenn wir noch einmal die Entfernung vom Punkt zur Ebene angeben möchten, tun wir dasselbe, passen jedoch die Entfernung an:
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
Das Gleiche mit einer Built-in-Funktion:
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
Dies wird wiederum entweder eine positive oder negative Distanz zurückliefern.
Das Umdrehen der Polarität der Ebene kann durch Negieren von N und D erfolgen. Dies führt zu einer Ebene an derselben Position, jedoch mit invertierten negativen und positiven Halbräumen:
N = -N
D = -D
N = -N;
D = -D;
Godot implementiert diesen Operator auch in Plane. Die Verwendung des folgenden Formats funktioniert also wie erwartet:
var inverted_plane = -plane
var invertedPlane = -plane;
Denken Sie also daran, dass der wichtigste praktische Nutzen der Ebene darin besteht, dass wir die Entfernung zu ihr berechnen können. Wann ist es also sinnvoll, die Entfernung zwischen einem Punkt und einer Ebene zu berechnen? Sehen wir uns einige Beispiele an.
Eine Ebene in 2D erstellen¶
Ebenen kommen natürlich nicht aus dem Nichts, also müssen sie gebaut werden. Das Konstruieren in 2D ist einfach. Dies kann entweder aus einer Normalen (Einheitsvektor) und einem Punkt oder aus zwei Punkten im Raum erfolgen.
Im Falle einer Normalen und eines Punktes ist die meiste Arbeit bereits getan, da die Normale bereits berechnet ist. Berechnen Sie also D aus dem Skalarprodukt der Normalen und des Punktes.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
Für zwei Punkte im Raum gibt es tatsächlich zwei Ebenen, die durch sie hindurchgehen und denselben Raum teilen, aber mit Normalen, die in entgegengesetzte Richtungen zeigen. Um die Normale aus den beiden Punkten zu berechnen, muss zuerst der Richtungsvektor ermittelt und dann um 90 ° nach beiden Seiten gedreht werden:
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
Der Rest ist dasselbe wie im vorherigen Beispiel. Entweder point_a oder point_b funktionieren, da sie in der gleichen Ebene liegen:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Das Gleiche in 3D zu tun, ist etwas komplexer und wird weiter unten erklärt.
Einige Beispiele von Ebenen¶
Hier ist ein Beispiel dafür, wozu Ebenen nützlich sind. Stellen Sie sich vor, Sie haben ein konvexes Polygon. Zum Beispiel ein Rechteck, ein Trapez, ein Dreieck oder einfach ein beliebiges Polygon, bei dem keine Fläche nach innen gebogen ist.
Für jedes Segment des Polygons berechnen wir die Ebene, die an diesem Segment vorbeigeht. Sobald wir die Liste der Ebenen haben, können wir tolle Dinge tun, zum Beispiel prüfen, ob sich ein Punkt innerhalb des Polygons befindet.
Wir gehen alle Ebenen durch. Wenn wir eine Ebene finden, deren Abstand zum Punkt positiv ist, liegt der Punkt außerhalb des Polygons, andernfalls liegt der Punkt innerhalb.
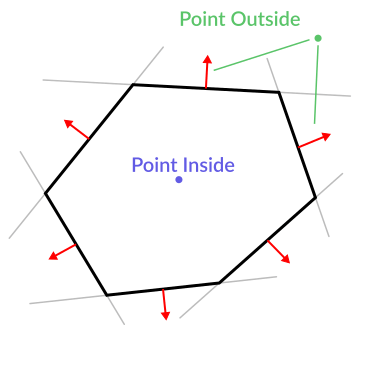
Der Code sollte ungefähr so aussehen:
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
Ziemlich cool, oder? Aber es wird noch viel besser! Mit etwas mehr Aufwand verrät uns eine ähnliche Logik, wann sich zwei konvexe Polygone überlappen. Dies wird als Separating Axis Theorem (SAT) bezeichnet, und die meisten Physik-Engines verwenden dies, um Kollisionen zu erkennen.
Bei einem Punkt reicht es aus, nur zu überprüfen, ob eine Ebene eine positive Entfernung zurückgibt, um festzustellen, ob der Punkt außerhalb liegt. Bei einem anderen Polygon müssen wir eine Ebene finden, in der alle anderen Polygon-Punkte einen positiven Abstand zurückgeben. Diese Prüfung wird mit den Ebenen von A gegen die Punkte von B und dann mit den Ebenen von B gegen die Punkte von A durchgeführt:
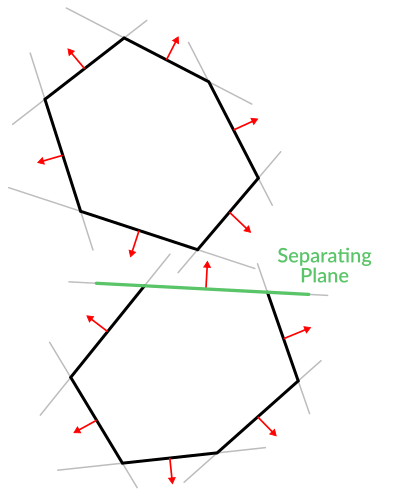
Der Code sollte ungefähr so aussehen:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Wie Sie sehen können, sind Ebenen sehr nützlich, und dies ist erst die Spitze des Eisbergs. Sie fragen sich vielleicht, was mit nicht konvexen Polygonen passiert. Dies wird in der Regel einfach durch Aufteilung des konkaven Polygons in kleinere konvexe Polygone oder durch eine Technik wie BSP bewerkstelligt (die heutzutage nicht mehr so häufig verwendet wird).
Kollisionserkennung in 3D¶
Jetzt kommt ein weiterer Bonus, eine Belohnung für die Geduld und das Durchhalten in diesem langen Tutorial. Hier ist ein weiterer kluger Ratschlag. Dies ist vielleicht nicht etwas für einen direkten Anwendungsfall (Godot macht Kollisionserkennung bereits ziemlich gut), aber es wird von fast allen Physik-Engines und Kollisionserkennungs-Bibliotheken verwendet :)
Erinnern Sie sich, dass das Konvertieren einer konvexen Form in 2D in ein Array von 2D-Ebenen für die Kollisionserkennung hilfreich war? Sie konnten feststellen, ob sich ein Punkt innerhalb einer konvexen Form befand oder ob sich zwei konvexe 2D-Formen überlappten.
Nun, dies funktioniert auch in 3D. Wenn zwei vielflächige 3D-Formen kollidieren, können Sie keine Trennebene finden. Wenn eine Trennebene gefunden wird, kollidieren die Formen definitiv nicht.
Zur Erinnerung: Trennebene bedeutet, dass sich alle Vertices des Polygons A auf einer Seite der Ebene und alle Vertices des Polygons B auf der anderen Seite befinden. Diese Ebene ist immer eine der Flächenebenen von Polygon A oder Polygon B.
In 3D gibt es jedoch ein Problem bei diesem Ansatz, da es möglich ist, dass in einigen Fällen keine Trennebene gefunden werden kann. Dies ist ein Beispiel für eine solche Situation:

Um dies zu vermeiden, müssen einige zusätzliche Ebenen als Trennobjekte getestet werden. Diese Ebenen sind das Kreuzprodukt zwischen den Kanten des Polygons A und den Kanten des Polygons B
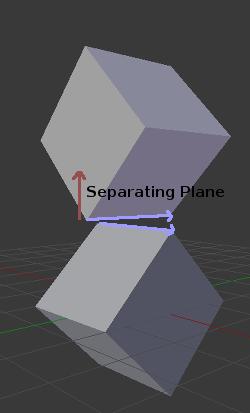
Der endgültige Algorithmus sieht also ungefähr so aus:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
Weitere Informationen¶
Für weitere Informationen zur Benutzung von Vektormathematik in Godot, siehe folgenden Artikel:
Wenn Sie weiterführende Erklärungen wünschen, sollten Sie sich die exzellente Videoserie "Essence of Linear Algebra" von 3Blue1Brown ansehen: https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab