Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Vektormathematik¶
Einführung¶
Dieses Tutorial ist eine kurze und praktische Einführung in die lineare Algebra, so wie sie in der Spielentwicklung benötigt wird. Lineare Algebra ist die Lehre von Vektoren und deren Nutzung. Vektoren haben viele Anwendungen in der 2D- und 3D-Entwicklung und Godot nutzt diese umfangreich. Für einen guten Spielentwickler ist es unverzichtbar, ein gutes Verständnis über Vektormathematik zu entwickeln.
Bemerkung
Dieses Tutorial ist kein formelles Lehrbuch über lineare Algebra, wir werden hier nur auf deren Anwendung bei der Spieleentwicklung eingehen. Für einen umfassenden Blick auf diesen Bereich der Mathematik siehe https://www.khanacademy.org/math/linear-algebra
Koordinatensysteme (2D)¶
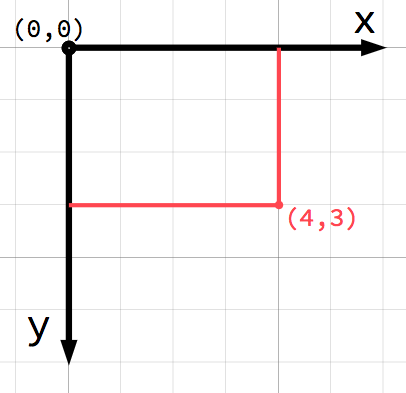
Im 2D-Raum werden die Koordinaten mittels einer horizontalen (x) und vertikalen (y) Achse definiert. Eine bestimmte Position im 2D-Raum wird als Wertepaar geschrieben, z.B. (4, 3).
Bemerkung
Es mag ungewöhnlich erscheinen, dass die positive y Achse nach unten zeigt anstatt nach oben, wie man es im Mathematikunterricht einmal gelernt hat. Dies ist aber normal in den meisten Computergrafik-Programmen.
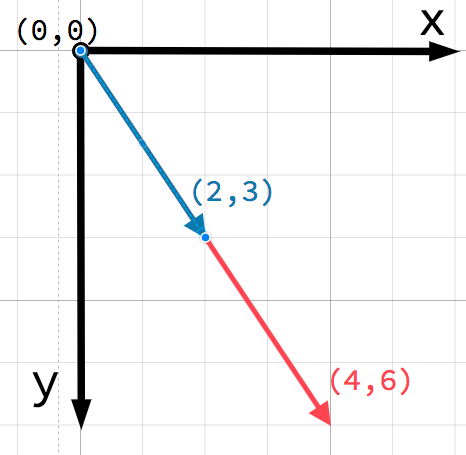
Jede Position im 2D-System kann über ein Zahlenpaar angesprochen werden. Man kann somit die Position (4, 3) als Versatz vom Ursprung (0, 0) ansehen. Hier sehen wir einen Pfeil vom Ursprung zum Punkt:
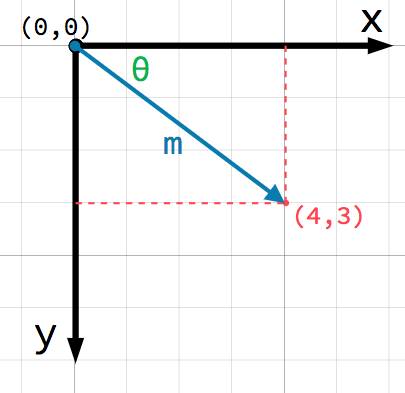
Dies ist ein Vektor. Ein Vektor repräsentiert eine Menge nützlicher Informationen. Er sagt uns nicht nur, dass der Punkt bei (4, 3) liegt, sondern wir können ihn uns auch als einen Winkel θ (Theta) und eine Länge (oder Betrag) m vorstellen. In diesem Fall ist der Pfeil ein Positionsvektor - er bezeichnet eine Position im Raum, bezogen auf den Ursprung.
Ein sehr wichtiger Punkt bei Vektoren ist, dass sie nur die relative Richtung und Betrag darstellen. Es gibt kein Konzept für die Position eines Vektors. Die folgenden zwei Vektoren sind identisch:
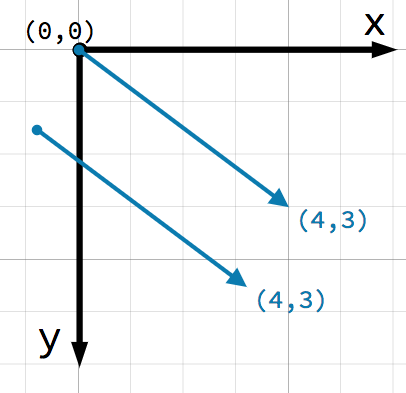
Beide Vektoren stellen einen Punkt dar, der 4 Einheiten nach rechts und 3 Einheiten unter einem Ausgangspunkt liegt. Es spielt keine Rolle, wo auf der Ebene Sie den Vektor zeichnen, er stellt immer eine relative Richtung und Betrag dar.
Vektoroperationen¶
Sie können jede der beiden Methoden (x- und y-Koordinaten oder Winkel und Betrag) verwenden, um sich auf einen Vektor zu beziehen, aber der Einfachheit halber verwenden Programmierer normalerweise die Koordinaten-Notation. Zum Beispiel ist in Godot der Ursprung die linke obere Ecke des Bildschirms. Um einen 2D-Node namens Node2D 400 Pixel nach rechts und 300 Pixel nach unten zu platzieren, verwenden Sie den folgenden Code:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot unterstützt sowohl Vector2 als auch Vector3 für den 2D- bzw. 3D-Gebrauch. Die gleichen mathematischen Regeln, die in diesem Artikel besprochen werden, gelten für beide Typen, und wo immer wir in der Klassenreferenz auf Vektor2-Methoden verweisen, können Sie auch deren Vektor3-Gegenstücke nachlesen.
Zugriff auf die Komponenten¶
Auf die einzelnen Komponenten des Vektors kann direkt über den Namen zugegriffen werden.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Vektoren addieren¶
Beim Addieren oder Subtrahieren zweier Vektoren werden die entsprechenden Komponenten addiert:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
Wir können dies auch visuell sehen, indem wir den zweiten Vektor an das Ende des ersten anhängen:
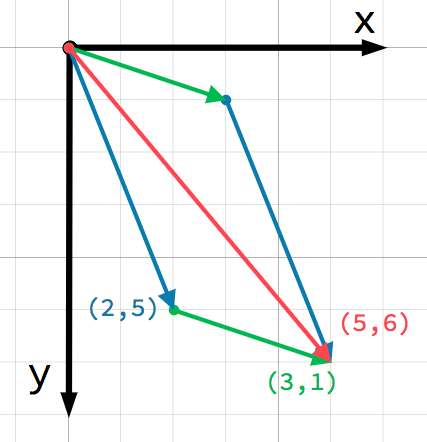
Beachten Sie, dass a + b zum gleichen Ergebnis führt wie b + a.
Skalarmultiplikation¶
Bemerkung
Vektoren stellen sowohl die Richtung als auch den Betrag dar. Ein Wert, der nur den Betrag darstellt, wird Skalar genannt. Skalare verwenden in Godot den Typ float.
Ein Vektor kann mit einen Skalar multipliziert werden:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Bemerkung
Die Multiplikation eines Vektors mit einem positiven Skalar ändert nicht seine Richtung, sondern nur seinen Betrag. Die Multiplikation mit einem negativen Skalar ergibt einen Vektor in umgekehrter Richtung. Auf diese Weise skaliert man einen Vektor.
Praktische Anwendungen¶
Sehen wir uns einmal zwei einfache Anwendungen zur Vektoraddition und -subtraktion an.
Bewegung¶
Ein Vektor kann jede Größe mit einem Betrag und einer Richtung darstellen. Typische Beispiele sind: Position, Geschwindigkeit, Beschleunigung und Kraft. In diesem Bild hat das Raumschiff bei Schritt 1 einen Positionsvektor von (1, 3) und einen Geschwindigkeitsvektor von (2, 1). Der Geschwindigkeitsvektor gibt an, wie weit sich das Raumschiff in jedem Schritt bewegt. Wir können die Position für Schritt 2 ermitteln, indem wir die Geschwindigkeit zur aktuellen Position addieren.
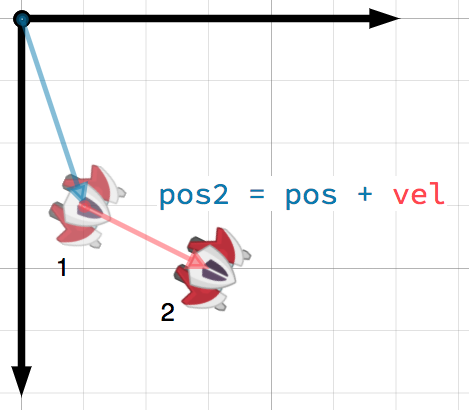
Tipp
Die Geschwindigkeit misst die Veränderung der Position pro Zeiteinheit. Die neue Position wird durch Addition der Geschwindigkeit multipliziert mit der verstrichenen Zeit (hier als eine Einheit angenommen, z.B. 1 s) zur vorherigen Position ermittelt.
In einem typischen 2D-Spielszenario würde man eine Geschwindigkeit in Pixeln pro Sekunde angeben und diese mit dem Parameter delta (die seit dem letzten Frame verstrichene Zeit) aus den _process() oder _physics_process()-Callbacks multiplizieren.
Ausrichtung auf ein Ziel¶
In diesem Szenario haben Sie einen Panzer, der seinen Turm auf einen Roboter richten möchte. Subtrahiert man die Position des Panzers von der Position des Roboters, erhält man den Vektor, der vom Panzer auf den Roboter zeigt.
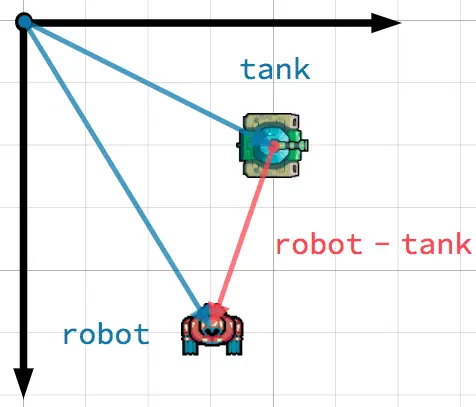
Tipp
Um einen Vektor zu finden, der von A nach B zeigt, benutzt man B - A.
Einheitsvektoren¶
Ein Vektor mit dem Betrag von 1 wird Einheitsvektor genannt. Sie werden manchmal auch als Richtungsvektoren oder Normalen bezeichnet. Einheitsvektoren sind hilfreich, wenn man eine Richtung festhalten muss.
Normierung¶
Normieren eines Vektors bedeutet, seine Länge auf 1 zu reduzieren und dabei seine Richtung beizubehalten. Dies geschieht, indem jede seiner Komponenten durch ihren Betrag dividiert wird. Weil dies eine so häufige Operation ist, bietet Godot eine eigene Methode normalisiert() dafür an:
a = a.normalized()
a = a.Normalized();
Warnung
Da bei der Normierung durch die Länge des Vektors dividiert wird, können Sie einen Vektor der Länge 0 nicht normieren. Der Versuch, dies zu tun, würde normalerweise zu einem Fehler führen. In GDScript bleibt der Wert jedoch unverändert, wenn man die Methode normalized() für einen Vektor der Länge 0 aufruft, so dass der Fehler nicht auftritt.
Reflexion¶
Eine häufige Verwendung von Einheitsvektoren ist die Angabe von Normalen. Normalenvektoren sind Einheitsvektoren, die senkrecht zu einer Oberfläche ausgerichtet sind und deren Richtung definieren. Sie werden häufig für Beleuchtung, Kollisionen und andere Operationen mit Oberflächen verwendet.
Stellen Sie sich zum Beispiel vor, Sie haben einen sich bewegenden Ball, den Sie an einer Wand oder einem anderen Objekt abprallen lassen wollen:
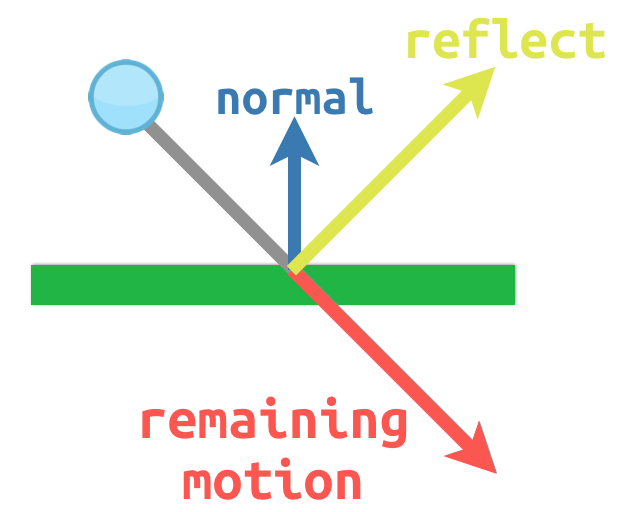
Die Oberflächennormale hat den Wert (0, -1), da es sich um eine horizontale Fläche handelt. Wenn der Ball aufprallt, nehmen wir seine verbleibende Bewegung (die Menge, die übrig bleibt, wenn er auf die Oberfläche trifft) und reflektieren sie mit Hilfe der Normalen. In Godot gibt es eine Methode bounce(), um dies zu behandeln. Hier ist ein Code-Beispiel für das obige Diagramm unter Verwendung eines CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Skalarprodukt¶
Das Skalarprodukt ist eines der wichtigsten Konzepte in der Vektormathematik, wird allerdings oft falsch verstanden. Das Skalarprodukt ist eine Operation auf zwei Vektoren, die einen Skalar ergibt. Im Gegensatz zu einem Vektor, der sowohl den Betrag als auch die Richtung enthält, hat ein Skalarwert nur einen Betrag.
Die Formel für das Skalarprodukt hat zwei übliche Formen:
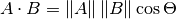
und
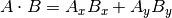
Die mathematische Notation ||A|| steht für den Betrag des Vektors A, und Ax bezeichnet die Komponente x des Vektors A.
In den meisten Fällen ist es jedoch am einfachsten, die built-in-Methode dot() zu verwenden. Beachten Sie, dass die Reihenfolge der beiden Vektoren keine Rolle spielt:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
Das Skalarprodukt ist am nützlichsten, wenn es mit Einheitsvektoren verwendet wird, wodurch sich die erste Formel auf cos(θ) reduziert. Das bedeutet, dass wir das Skalarprodukt verwenden können, um uns etwas über den Winkel zwischen zwei Vektoren auszusagen:
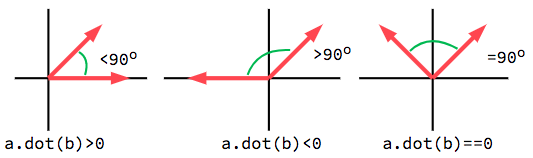
Bei Verwendung von Einheitsvektoren liegt das Ergebnis immer zwischen -1 (180°) und 1 (0°).
Blickrichtung¶
Wir können diese Tatsache nutzen, um festzustellen, ob ein Objekt einem anderen Objekt zugewandt ist. In der folgenden Abbildung versucht der Spieler P, den Zombies A und B auszuweichen. Angenommen, das Sichtfeld eines Zombies ist 180°, können sie den Spieler sehen?
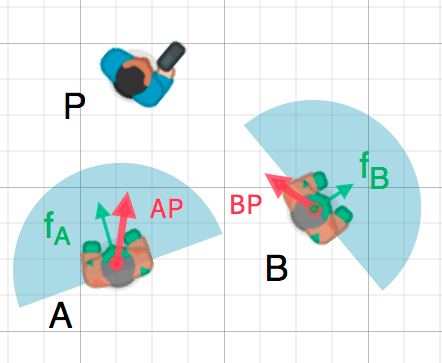
Die grünen Pfeile fA und fB sind Einheitsvektoren, und stellen die Blickrichtung des Zombies dar, und der blaue Halbkreis repräsentiert sein Sichtfeld. Für den Zombie A finden wir den Richtungsvektor AP, der auf den Spieler zeigt, indem wir P - A verwenden und ihn normieren. Godot hat dafür eine Hilfsmethode namens direction_to(). Wenn der Winkel zwischen diesem Vektor und dem gegenüberliegenden Vektor kleiner als 90° ist, kann der Zombie den Spieler sehen.
Der entsprechende Code sieht so aus:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Kreuzprodukt¶
Wie das Skalarprodukt ist das Kreuzprodukt eine Operation auf zwei Vektoren. Das Ergebnis des Kreuzprodukts ist jedoch ein Vektor mit einer Richtung, die senkrecht zu beiden ist. Ihr Betrag hängt von ihrem relativen Winkel ab. Wenn zwei Vektoren parallel sind, ist das Ergebnis ihres Kreuzprodukts ein Nullvektor.

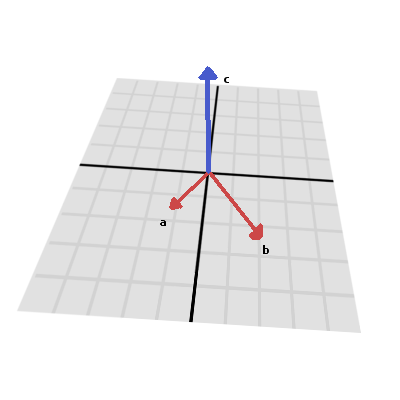
Das Kreuzprodukt wird wie folgt berechnet:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
Mit Godot können Sie die Built-in-Methode Vector3.cross() verwenden:
var c = a.cross(b)
var c = a.Cross(b);
Das Kreuzprodukt ist in 2D nicht mathematisch definiert. Die Methode Vector2.cross() ist ein häufig verwendetes Analogon des 3D-Kreuzprodukts für 2D-Vektoren.
Bemerkung
Im Kreuzprodukt ist die Reihenfolge wichtig. a.cross(b) liefert nicht das gleiche Ergebnis wie b.cross(a). Die resultierenden Vektoren zeigen in entgegengesetzte Richtungen.
Normalen berechnen¶
Eine häufige Anwendung von Kreuzprodukten ist die Ermittlung der Flächennormalen einer Ebene oder Fläche im 3D-Raum. Wenn wir das Dreieck ABC haben, können wir die Vektorsubtraktion verwenden, um zwei Kanten AB und AC zu finden. Mit dem Kreuzprodukt AB × AC erhält man einen Vektor, der senkrecht zu beiden Kanten steht: die Oberflächennormale.
Hier ist eine Funktion zur Bestimmung der Normalen eines Dreiecks:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Auf ein Ziel ausrichten¶
Im obigen Abschnitt über das Skalarprodukt haben wir gesehen, wie damit der Winkel zwischen zwei Vektoren ermittelt werden kann. In 3D reichen diese Informationen jedoch nicht aus. Wir müssen auch wissen, um welche Achse wir uns drehen müssen. Wir können dies feststellen, indem wir das Kreuzprodukt der aktuellen Blickrichtung und der Zielrichtung berechnen. Der resultierende senkrechte Vektor ist die Rotationsachse.
Weitere Informationen¶
Für weitere Informationen über Vektormathematik in Godot siehe die folgenden Artikel: