Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
高度なベクトル演算¶
平面(およびplane関数)¶
ドット積には、単位ベクトルに関する別の興味深い特性があります。そのベクトルに垂直な (そして原点を通る) 平面を通過すると想像してください。平面は空間全体を正(平面上)と負(平面下)に分割し、(一般的な信念に反して)2Dで計算をすることもできます:
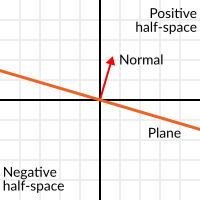
サーフェスに対して垂直な(したがって、サーフェスの方向を表す)単位ベクトルは 単位法線ベクトル(unit normal vectors) と呼ばれます。ただし、通常は 法線(normal) と省略されます。法線は平面、3Dジオメトリ(各面または頂点のサイディングの位置を決定するため)などに表示されます。法線 は 単位ベクトル ですが、その使用上は 法線 と呼ばれています。(普通に(0,0)をオリジンと呼んでいるのと同様に!)。
The plane passes by the origin and the surface of it is perpendicular to the unit vector (or normal). The side towards the vector points to is the positive half-space, while the other side is the negative half-space. In 3D this is exactly the same, except that the plane is an infinite surface (imagine an infinite, flat sheet of paper that you can orient and is pinned to the origin) instead of a line.
平面までの距離¶
平面が何であるかが明確になったので、ドット積に戻りましょう。単位ベクトル と空間内の ポイント 間のドット積(今回はベクトルと位置の間のドット積を行います)は、ポイントから平面までの距離 を返します:
var distance = normal.dot(point)
var distance = normal.Dot(point);
ただし、符号のない絶対距離ではなく、ポイントが負の半空間にある場合は、距離も負になります:
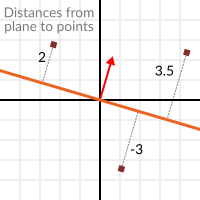
これにより、ポイントが平面のどちら側にあるかを知ることができます。
原点から離れて¶
私はあなたが何を考えているか知っています!これまでのところ、これは素晴らしいですが、実際の平面は、原点を通過するだけでなく、空間のいたるところにあります。あなたは本当の 平面 アクションを、まさに今望んでいるはすです。
平面は空間を2つに分割するだけでなく、極性も持っていることに注意してください。これは、完全にオーバーラップする平面を持つことは可能ですが、負と正の半空間が入れ替わりうることを意味します。
これを念頭に置いて、完全な平面を法線 N および原点からの距離スカラー D として説明しましょう。したがって、平面はNとDで表されます。たとえば、次のとおりです:
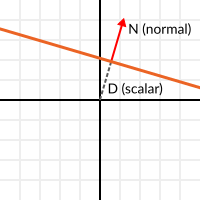
3D演算の場合、Godotはこれを処理する組み込み型 Plane を提供します。
基本的に、NとDは2Dでも3Dでも(Nの次元の量に応じて)空間内の任意の平面を表すことができ、数学は両方で同じです。前と同じですが、Dは原点から平面までの距離で、N方向に移動します。例として、平面のある地点に到達したい場合、次のようにします:
var point_in_plane = N*D
var pointInPlane = N * D;
これにより、法線ベクトルが伸縮(サイズ変更)され、平面に接触します。この数学は混乱しているように見えるかもしれませんが、実際には見かけよりもはるかに簡単です。もう一度、ポイントから平面までの距離を伝えたい場合は、距離を調整しながら同じことを行います:
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
同じことを、組み込み関数を使用すると:
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
これもまた、正または負の距離を返します。
平面の極性を反転させるには、NとDの両方を反極性にします(+-の反転)。これにより、平面は同じ位置になりますが、負と正の半空間が逆になります:
N = -N
D = -D
N = -N;
D = -D;
Godot also implements this operator in Plane. So, using the format below will work as expected:
var inverted_plane = -plane
var invertedPlane = -plane;
So, remember, the plane's main practical use is that we can calculate the distance to it. So, when is it useful to calculate the distance from a point to a plane? Let's see some examples.
2Dで平面を構築する¶
平面は明らかにどこからともなく出てはこないので、構築する必要があります。それらを2Dで作成するのは簡単です。これは、法線(単位ベクトル)と点、または空間内の2つの点のいずれかから実行できます。
In the case of a normal and a point, most of the work is done, as the normal is already computed, so calculate D from the dot product of the normal and the point.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
空間内の2つのポイントには、それらを通過する2つの平面があり、同じ空間を共有しますが、法線は反対方向を指します。 2点から法線を計算するには、最初に方向ベクトルを取得してから、どちらかの側に90度回転する必要があります:
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
The rest is the same as the previous example. Either point_a or point_b will work, as they are in the same plane:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Doing the same in 3D is a little more complex and is explained further down.
平面処理に関するいくつかの例¶
Here is an example of what planes are useful for. Imagine you have a convex polygon. For example, a rectangle, a trapezoid, a triangle, or just any polygon where no faces bend inwards.
ポリゴンのすべてのセグメントについて、そのセグメントを通過する平面を計算します。平面のリストを取得したら、あるポイントがポリゴン内にあるかどうかを確認するなどの、きちんとした操作を行うことができます。
ポイントまでの距離が正である平面を一つでも見つけることができれば、ポイントはポリゴンの外側にあります。できない場合、ポイントはポリゴンの内側にあります。
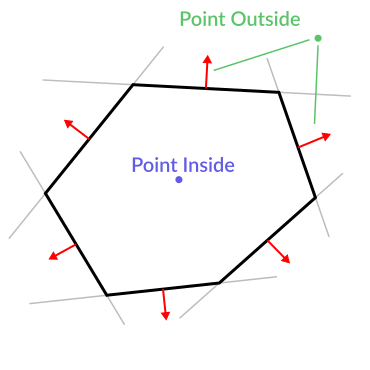
コードは次のようになります:
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
すごくクールですか?しかし、これははるかに良くできます!もう少し努力すれば、同様のロジックを使用して、2つの凸ポリゴンが重なっていることがわかります。これは分離軸定理(またはSAT)と呼ばれ、ほとんどの物理エンジンはこれを使用して衝突を検出します。
ポイントの場合、平面までの距離が正の値を返すかどうかを確認するだけで、ポイントが外側にあるかどうかを判断できます。別ポリゴンの場合は、そのポリゴンの全ての点が正の距離を返す平面を見つける必要があります。このチェックは、Aの平面に対するBのポイントを対象に実行され、次にBの平面に対するAのポイントに対象に実行されます:
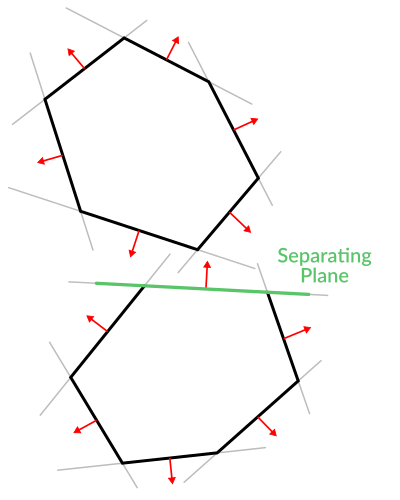
コードは次のようになります:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
ご覧のとおり、平面処理関数は非常に便利です。これが氷山の一角です。非凸ポリゴンで何が起こるか疑問に思うかもしれません。これは通常、凹面のポリゴンをより小さな凸面のポリゴンに分割するか、BSP(バイナリ空間分割、最近ではあまり使用されていない)などの手法を使用して処理されます。
3Dでの衝突検出¶
これはもう1つのボーナスです。辛抱強く、この長いチュートリアルに遅れずについていくことに対する報酬です。ここにもう一つの知恵があります。これは直接的な使用例ではないかもしれませんが(Godotはすでに衝突検出をかなりうまく行います)、ほとんどすべての物理エンジンと衝突検出ライブラリで使用されています(^^)
2Dの凸形状を2D平面の配列に変換することは、衝突検出に役立つことを覚えていますか?点が凸形状の内側にあるか、2つの2D凸形状が重なっているかを検出できます。
そう、これは3Dでも機能します。2つの3D多面体形状が衝突している場合、分離平面を見つけることができません。分離平面が見つかった場合は、形状は明らかに衝突していません。
分離平面に関する考えを少し更新すると、ポリゴンAのすべての頂点がその平面の片側にあり、ポリゴンBのすべての頂点が反対側にあることを意味します。この平面は、常にポリゴンAまたはポリゴンBのいずれかの面平面の1つです。
ただし、3Dでは、このアプローチには問題があります。これは、場合によっては分離平面が見つからない可能性があるためです。これはそのような状況の例です:

それを回避するには、いくつかの余分な平面をセパレータとしてテストする必要があります。これらの平面は、ポリゴンAのエッジとポリゴンBのエッジ間の外積です
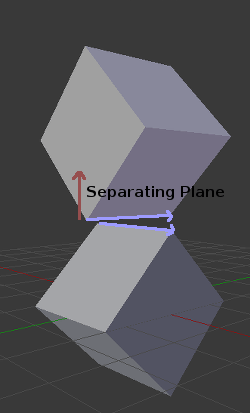
したがって、最終的なアルゴリズムは次のようになります:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
より多くの情報¶
For more information on using vector math in Godot, see the following article:
If you would like additional explanation, you should check out 3Blue1Brown's excellent video series "Essence of Linear Algebra": https://www.youtube.com/watch?v=fNk_zzaMoSs&list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab