Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
贝塞尔、曲线和路径¶
贝塞尔曲线是一种自然几何形状的数学近似. 我们用它们来代表一个曲线, 含有尽可能少的信息, 保持高水平的灵活性.
不像抽象的数学概念, 贝塞尔曲线是为工业设计. 它们是图形软件行业中的流行工具.
它们依赖于 插值, 我们在上一篇文章中看到, 如何结合多个步骤来创建平滑的曲线. 为了更好地理解贝塞尔曲线的工作原理, 我们从最简单的形式开始: 二次贝塞尔曲线.
二次贝塞尔曲线¶
取三个点, 这是建立二次贝塞尔曲线所需的最小值:
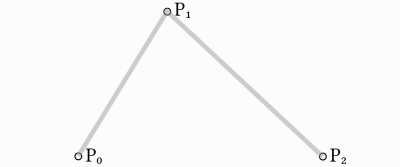
要在它们之间画一条曲线,我们首先使用 0 到 1 之间的值,在由这三个点构成的两个线段的每个顶点上逐步插值。当我们把 t 值从 0 变成 1 时,就得到了两个沿着线段移动的点。
func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
}
然后,我们插值 q0 和 q1,以获得沿着曲线移动的单点 r。
var r = q0.lerp(q1, t)
return r
Vector2 r = q0.Lerp(q1, t);
return r;
这种类型的曲线就被称为二次贝塞尔曲线。
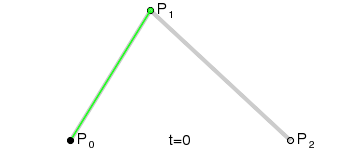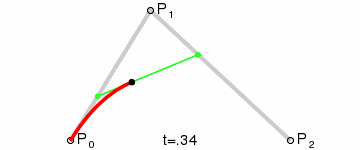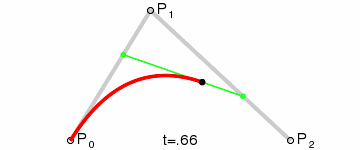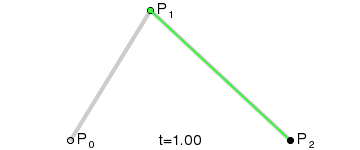
(图像来源: 维基百科)
三次贝塞尔曲线¶
基于前面的例子, 我们可以通过在四个点之间插值得到更多的控制.
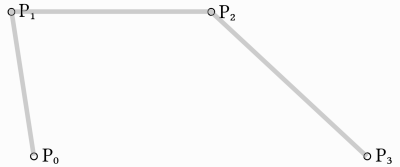
首先我们使用一个带有四个参数的函数,以 p0、p1、p2、p3 四个点作为输入:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
}
我们对每两个点进行线性插值, 将它们减少到三个:
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
然后我们把这三个点缩减为两个点:
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
然后到一个:
var s = r0.lerp(r1, t)
return s
Vector2 s = r0.Lerp(r1, t);
return s;
这里给出了完整的函数:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
var s = r0.lerp(r1, t)
return s
private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Vector2 s = r0.Lerp(r1, t);
return s;
}
结果将是在所有四个点之间的平滑曲线插值:
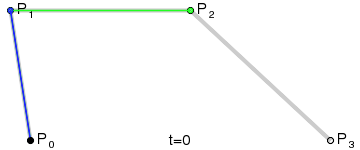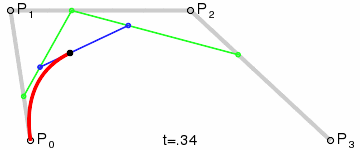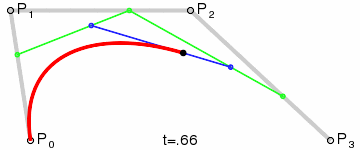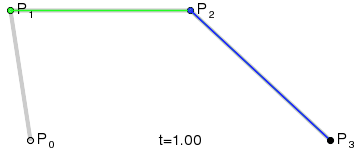
(图像来源: 维基百科)
备注
三次贝塞尔插值在三维中也是一样的,只需使用 Vector3 代替 Vector2。
添加控制点¶
在三次贝塞尔的基础上,我们可以通过改变两个点的工作方式来自由地控制曲线的形状。我们不使用 p0、p1、p2、p3,而是将它们存储为:
point0 = p0:是第一个点,即源control0 = p1 - p0:是相对于第一个控制点的向量control1 = p3 - p2:是相对于第二个控制点的向量point1 = p3:是第二个点,即终点
使用这种方式, 有两个点和两个控制点, 它们是各自点的相对向量. 如果你以前用过图形或动画软件, 这可能看起来很熟悉:
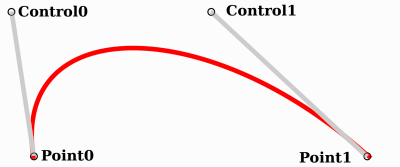
这就是图形软件如何向用户呈现贝塞尔曲线, 以及它们在Godot引擎内的工作原理.
Curve2D、Curve3D、Path 以及 Path2D¶
有两个对象包含曲线 Curve3D 和 Curve2D(分别代表 3D 和 2D)。
They can contain several points, allowing for longer paths. It is also possible to set them to nodes: Path3D and Path2D (also for 3D and 2D respectively):
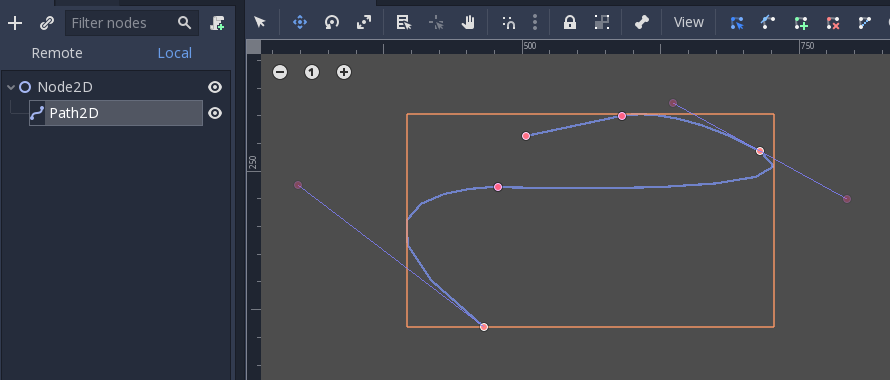
然而它们的使用方法可能不是很直观,下面是对贝塞尔曲线最常见用例的描述。
估值¶
Only evaluating them may be an option, but in most cases it's not very useful. The big drawback with Bezier curves is that if you traverse them at constant speed, from t = 0 to t = 1, the actual interpolation will not move at constant speed. The speed is also an interpolation between the distances between points p0, p1, p2 and p3 and there is not a mathematically simple way to traverse the curve at constant speed.
Let's do an example with the following pseudocode:
var t = 0.0
func _process(delta):
t += delta
position = _cubic_bezier(p0, p1, p2, p3, t)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = CubicBezier(p0, p1, p2, p3, _t);
}

如你所见,即便 t 在匀速递增,圆点的速度还是在不断变化的(以像素每秒为单位)。这也使贝塞尔难以做到任何实际的开箱即用。
绘制¶
绘制贝塞尔(或基于曲线的对象)是很常见的用例, 但这也不容易. 几乎在任何情况下, 贝塞尔曲线需要被转换成某种线段. 这通常很难, 然而, 并没有创建非常高数量的线段.
原因是曲线的某些部分(具体来说是角落)可能需要相当多的点, 而其他部分不一定:

另外,如果两个控制点都是 0,0(请记住它们是相对向量),贝塞尔曲线就是一条直线(所以画很多点就是在浪费时间)。
在绘制贝塞尔曲线之前, 需要进行 细分 . 这通常是用递归函数或除法函数来完成的, 它可以分割曲线, 直到曲率变得小于某个阈值.
Curve 类通过 Curve2D.tessellate() 函数来提供该功能(函数接收可选的 stages 递归和角度 tolerance 参数). 这样一来, 基于曲线画东西就比较容易了.
遍历¶
最后曲线最常见的用例是遍历. 因为之前提到关于匀速的内容, 这也是困难的.
To make this easier, the curves need to be baked into equidistant points. This way, they can be approximated with regular interpolation (which can be improved further with a cubic option). To do this, just use the Curve3D.sample_baked() method together with Curve2D.get_baked_length(). The first call to either of them will bake the curve internally.
匀速遍历, 然后, 可以用下面的伪代码:
var t = 0.0
func _process(delta):
t += delta
position = curve.sample_baked(t * curve.get_baked_length(), true)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}
并且输出, 然后匀速移动:
