Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
向量数学¶
前言¶
本教程是一个简短而实用的线性代数介绍,因为它适用于游戏开发。线性代数是研究向量及其用途的学科。向量在 2D 和 3D 开发中都有许多应用,Godot 对它们的应用也非常广泛。要成为一名优秀的游戏开发者,对向量数学的理解是必不可少的。
备注
本教程不是线性代数的正式教科书。我们将只关注它如何应用于游戏开发。要更全面地了解数学,请参见 https://www.khanacademy.org/math/linear-algebra
坐标系(2D)¶
在 2D 空间中,使用水平轴(x)和垂直轴(y)定义坐标。2D 空间中的特定位置会被写成一对值,如 (4, 3)。
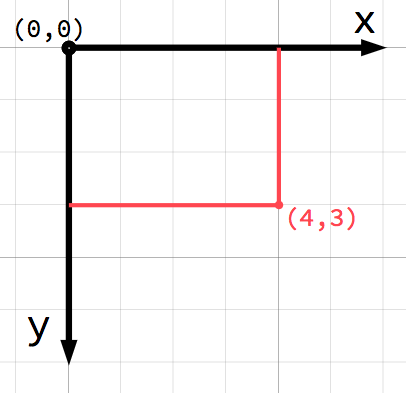
备注
如果你是计算机图形学的新手,可能会觉得很奇怪,y 轴的正方向朝下而不是向上(你在数学课上学到的就像那样)。然而,这在大多数计算机图形应用程序中是常见的。
2D 平面上的任何位置都可以用一对数字来表示。然而,我们也可以将位置 (4, 3) 看作是从 (0, 0) 点或原点出发的偏移。画一个箭头从原点指向点:
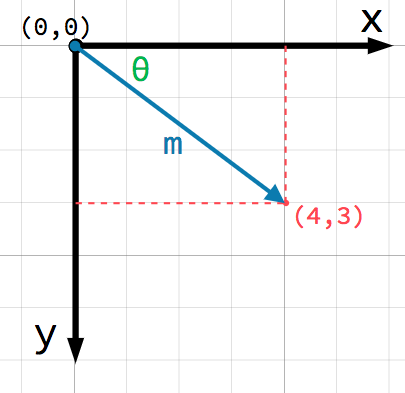
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
关于向量, 需要考虑的一个重要点是它们仅表示 相对 方向和大小. 没有一个向量的位置的概念. 以下两个向量相同:
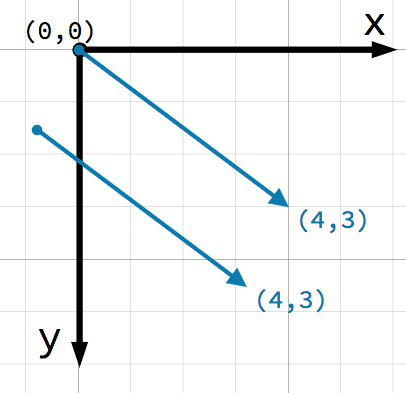
这两个向量都表示向右4个单位, 在某个起始点以下3个单位. 不管你在平面上画哪个向量, 它总是代表一个相对的方向和大小.
向量运算¶
你可以使用任意一种方法,x和y坐标或角度和大小, 来引用向量, 但是为了方便起见, 程序员通常使用坐标表示法. 例如, 在Godot中, 原点是屏幕左上角, 因此要将一个名为 Node2D 的2D节点向右400像素, 向下300像素, 请使用以下代码:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
成员访问¶
向量的各个组成部分可以直接通过名称访问.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
向量加法¶
当两个向量相加或相减时, 相应的分量相加:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
我们也可以通过在第一个向量的末尾加上第二个向量来直观地看到这一点:
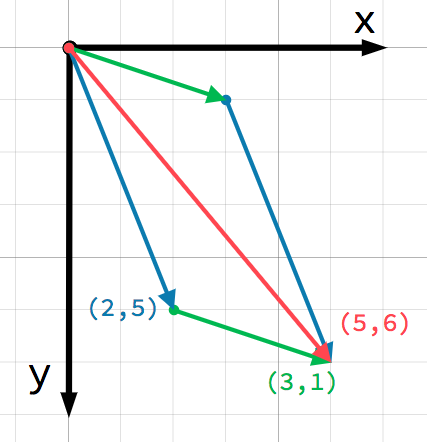
注意,做 a + b 的加法和 b + a 得到的结果是一样的。
标量乘法¶
备注
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
向量可以乘以标量:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
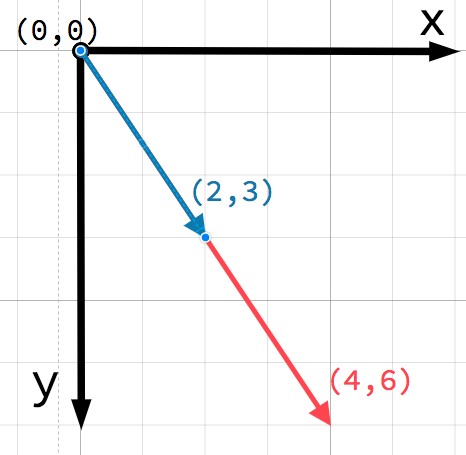
备注
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
实际应用¶
让我们看看向量加法和减法的两种常见用法.
移动¶
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
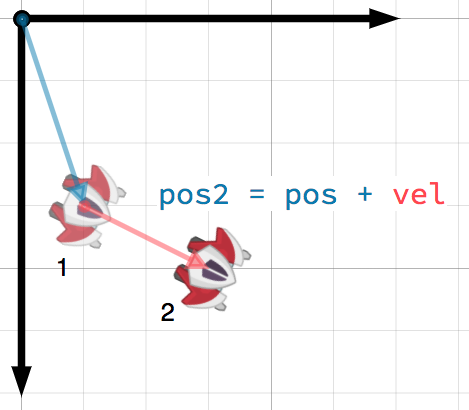
小技巧
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
指向目标¶
在这个场景中,你有一辆坦克,坦克希望让炮塔指向机器人。把机器人的位置减去坦克的位置就得到了从坦克指向机器人的向量。
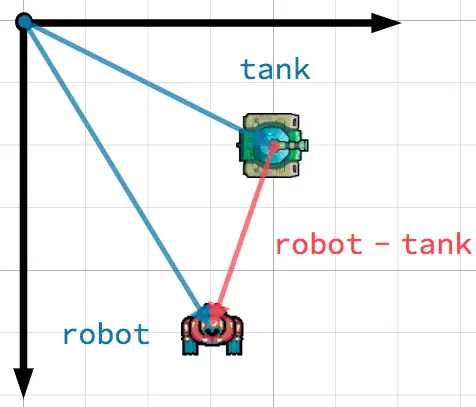
小技巧
To find a vector pointing from A to B, use B - A.
单位向量¶
大小为 1 的向量称为单位向量,有时也被称为方向向量或法线。当你需要记录方向时就可以使用单位向量。
归一化¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
警告
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
反射¶
单位向量的一种常见用法是表示法线。法向量是垂直于表面的单位向量,定义了表面的方向。它们通常用于照明、碰撞和涉及表面的其他操作。
例如, 假设我们有一个移动的球, 我们想从墙上或其他物体上弹回来:
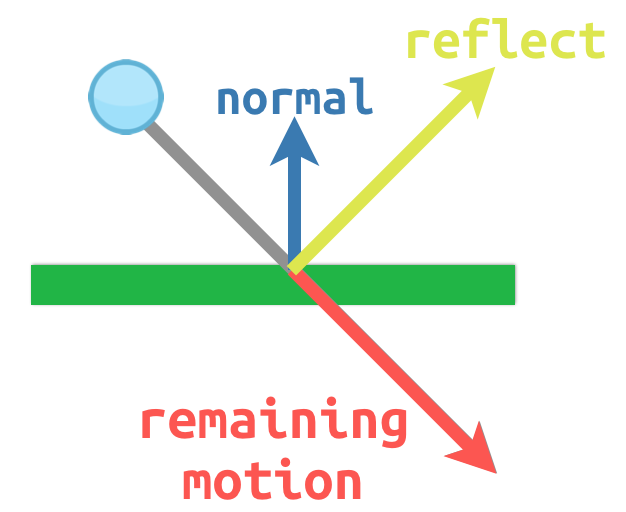
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
点积¶
点积是向量数学中最重要的概念之一,但经常被误解。点积是对两个向量的操作,返回一个标量。与同时包含大小和方向的向量不同,标量值只有大小。
点积公式有两种常见形式:
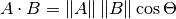
以及
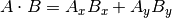
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
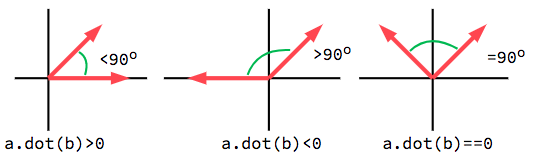
当使用单位向量, 结果总是会在 -1 (180°) 和 1 (0°) 之间.
面向问题¶
我们可以利用这个事实来检测一个物体是否面向另一个物体. 在下图中, 游戏角色 P 试图避开丧尸 A 和 B . 假设一个丧尸的视野是 180° , 他们能看到游戏角色吗?
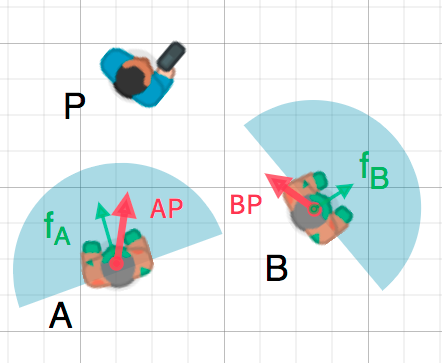
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
在代码中是这样的:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
叉积¶
和点积一样,叉积也是对两个向量的运算。但是,叉乘积的结果是一个方向与两个向量垂直的向量。它的大小取决于相对角度,如果两个向量是平行的,那么叉积的结果将是一个空向量。

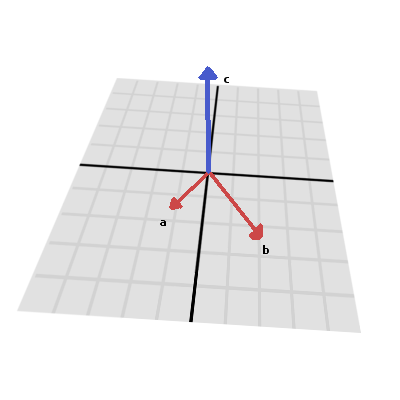
叉积是这样计算的:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
备注
在叉积中,顺序很重要。a.cross(b) 和 b.cross(a) 的结果不一样,会得到指向相反的向量。
法线计算¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
下面是一个计算三角形法线的函数:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
指向目标¶
在上面的点积部分,我们看到如何用它来查找两个向量之间的角度。然而在 3D 中,这些信息还不够。我们还需要知道在围绕什么轴旋转。我们可以通过计算当前面对的方向和目标方向的叉积来查找。由此得到的垂直向量就是旋转轴。
更多信息¶
有关在Godot中使用向量数学的更多信息, 请参阅以下文章: