Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Beziers, curvas y caminos¶
Las curvas de Bezier son una aproximación matemática de las formas geométricas naturales. Las utilizamos para representar una curva con la menor información posible y con un alto nivel de flexibilidad.
A diferencia de los conceptos matemáticos más abstractos, las curvas de Bezier fueron creadas para el diseño industrial. Son una herramienta popular en la industria del software gráfico.
Se basan en interpolation, que vimos en el artículo anterior, combinando múltiples pasos para crear curvas suaves. Para entender mejor cómo funcionan las curvas de Bezier, empecemos por su forma más simple: Bezier Cuadrática.
Bezier Cuadrática¶
Toma tres puntos, el mínimo requerido para que funcione la Bezier Cuadrática:
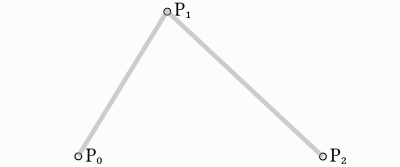
Para dibujar una curva entre ellos, primero interpolamos gradualmente sobre los dos vértices de cada uno de los dos segmentos formados por tres puntos, usando valores que van del 0 al 1. Esto nos da dos puntos que se mueven a lo largo de los segmentos a medida que cambiamos el valor de t del 0 al 1.
func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
}
Luego interpolamos q0 y q1 para obtener un único punto r que se mueve a lo largo de una curva.
var r = q0.lerp(q1, t)
return r
Vector2 r = q0.Lerp(q1, t);
return r;
Este tipo de curva se llama curva de Bezier Cuadrática.
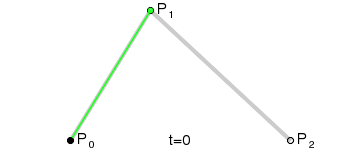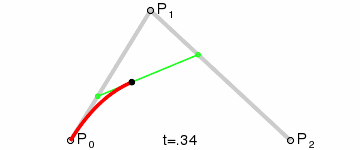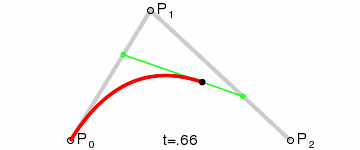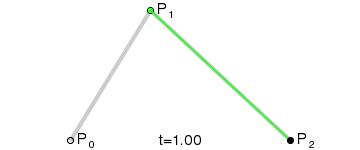
(Crédito de la imagen: Wikipedia)
Bezier Cúbico¶
Basándonos en el ejemplo anterior, podemos obtener más control interpolando entre cuatro puntos.
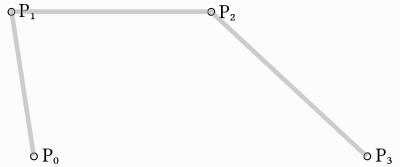
Primero usamos una función con cuatro parámetros para tomar cuatro puntos como entrada, p0, p1, p2 y p3:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
}
Aplicamos una interpolación lineal a cada par de puntos para reducirlos a tres:
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Luego tomamos nuestros tres puntos y los reducimos a dos:
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Y a uno:
var s = r0.lerp(r1, t)
return s
Vector2 s = r0.Lerp(r1, t);
return s;
Aquí está la función completa:
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
var s = r0.lerp(r1, t)
return s
private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Vector2 s = r0.Lerp(r1, t);
return s;
}
El resultado será una curva suave que interpola entre los cuatro puntos:
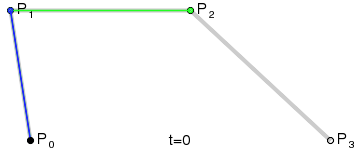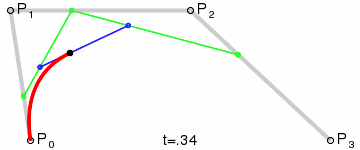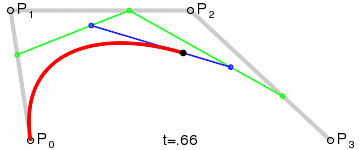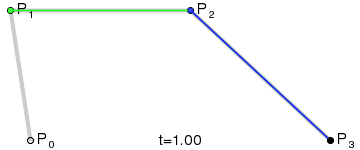
(Crédito de la imagen: Wikipedia)
Nota
La interpolación de Bezier Cúbica funciona igual en 3D, sólo que usa Vector3 en lugar de Vector2.
Agregando puntos de control¶
Basándonos en la Bezier Cúbica, podemos cambiar la forma en que dos de los puntos funcionan para controlar la forma de nuestra curva libremente. En lugar de tener p0, p1, p2 y p3, los guardaremos como:
point0 = p0: Es el primer punto, la fuentecontrol0 = p1 - p0: Es un vector relativo al primer punto de controlcontrol1 = p3 - p2: Es un vector relativo al segundo punto de controlpoint1 = p3: Es el segundo punto, el destino
De esta manera, tenemos dos puntos y dos puntos de control que son vectores relativos a los respectivos puntos. Si has usado software de gráficos o de animación antes, esto puede resultar familiar:
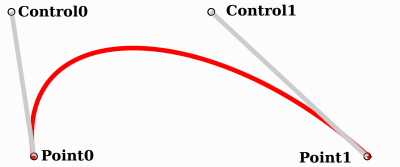
Así es como el software de gráficos presenta las curvas de Bezier a los usuarios, y cómo funcionan y se ven en Godot.
Curve2D, Curve3D, Path y Path2D¶
Existen dos objetos que contienen curvas: Curve3D y Curve2D (para 3D y 2D respectivamente).
They can contain several points, allowing for longer paths. It is also possible to set them to nodes: Path3D and Path2D (also for 3D and 2D respectively):
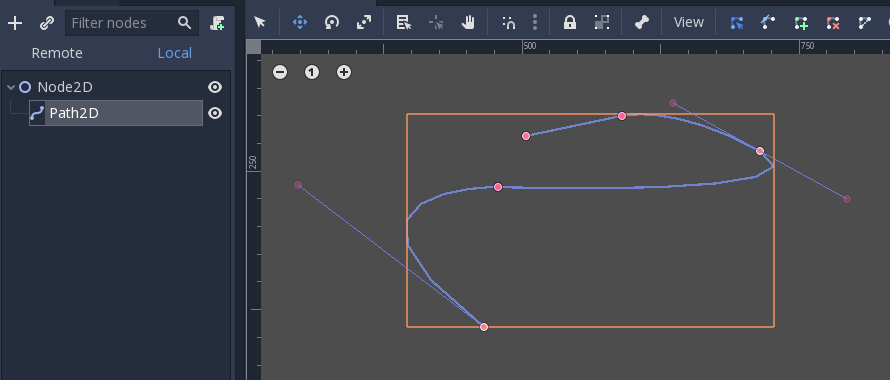
Sin embargo, su uso puede no ser completamente obvio, por lo que a continuación se describen los casos de uso más comunes de las curvas de Bezier.
Evaluando¶
Only evaluating them may be an option, but in most cases it's not very useful. The big drawback with Bezier curves is that if you traverse them at constant speed, from t = 0 to t = 1, the actual interpolation will not move at constant speed. The speed is also an interpolation between the distances between points p0, p1, p2 and p3 and there is not a mathematically simple way to traverse the curve at constant speed.
Let's do an example with the following pseudocode:
var t = 0.0
func _process(delta):
t += delta
position = _cubic_bezier(p0, p1, p2, p3, t)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = CubicBezier(p0, p1, p2, p3, _t);
}

Como puedes ver, la velocidad (en píxeles por segundo) del círculo varía, aunque t se incrementa a velocidad constante. Esto hace que las beziers sean difíciles de usar para cualquier cosa práctica fuera de la caja.
Dibujando¶
Dibujar beziers (u objetos basados en la curva) es un caso de uso muy común, pero tampoco es fácil. En casi todos los casos, las curvas Bezier deben ser convertidas en algún tipo de segmento. Sin embargo, esto normalmente es difícil sin crear una cantidad muy alta de ellos.
La razón es que algunas secciones de una curva (específicamente, las esquinas) pueden requerir cantidades considerables de puntos, mientras que otras secciones pueden no necesitarlos:

Además, si ambos puntos de control fueran 0, 0 (recuerda que son vectores relativos), la curva de Bezier sería sólo una línea recta (por lo que dibujar una gran cantidad de puntos sería un desperdicio).
Antes de dibujar las curvas de Bezier, se requiere un teselado. Esto se hace a menudo con una función recursiva o de dividir y conquistar que divide la curva hasta que la cantidad de curvatura se vuelve menor que un cierto umbral.
Las clases Curve proporcionan esto a través de la función Curve2D.tessellate() (que recibe los argumentos opcionales stages de recursividad y ángulo de tolerance). De esta manera, dibujar algo basado en una curva es más fácil.
Traversal¶
El último caso de uso común de las curvas es atravesarlas. Debido a lo que se mencionó antes sobre la velocidad constante, esto también es difícil.
To make this easier, the curves need to be baked into equidistant points. This way, they can be approximated with regular interpolation (which can be improved further with a cubic option). To do this, just use the Curve3D.sample_baked() method together with Curve2D.get_baked_length(). The first call to either of them will bake the curve internally.
Travesía a velocidad constante, entonces, puede hacerse con el siguiente pseudo-código:
var t = 0.0
func _process(delta):
t += delta
position = curve.sample_baked(t * curve.get_baked_length(), true)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}
Y la salida, entonces, se moverá a velocidad constante:
