Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Béziers, courbes et chemins¶
Les courbes de Bézier sont une approximation mathématique des formes géométriques naturelles. Nous les utilisons pour représenter une courbe avec le moins d'informations possible et avec un haut niveau de flexibilité.
Contrairement aux concepts mathématiques plus abstraits, les courbes de Bézier ont été créées pour le design industriel. Ils sont un outil populaire dans l'industrie des logiciels graphiques.
Ils s'appuient sur l'interpolation, que nous avons vu dans l'article précédent, combinant plusieurs étapes pour créer des courbes lisses. Pour mieux comprendre le fonctionnement des courbes de Bézier, partons de sa forme la plus simple : Bézier quadratique.
Bézier quadratique¶
Prenez trois points, le minimum requis pour que le Bézier quadratique fonctionne :
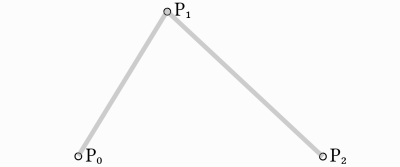
Pour tracer une courbe entre eux, nous interpolons d'abord progressivement sur les deux sommets de chacun des deux segments formés par les trois points, en utilisant des valeurs allant de 0 à 1, ce qui nous donne deux points qui se déplacent le long des segments à mesure que nous changeons la valeur de t de 0 à 1.
func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
}
Nous interpolons ensuite q0 et q1 pour obtenir un point unique r qui se déplace le long d'une courbe.
var r = q0.lerp(q1, t)
return r
Vector2 r = q0.Lerp(q1, t);
return r;
Ce type de courbe s'appelle une courbe de Bézier quadratique.
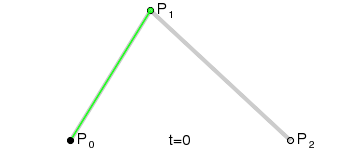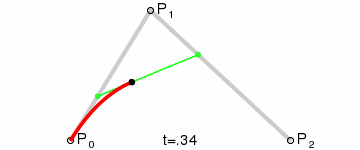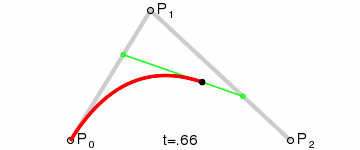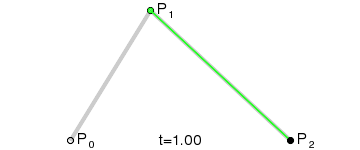
(Crédit image : Wikipedia)
Bézier cubique¶
En nous basant sur l'exemple précédent, nous pouvons obtenir plus de contrôle en interpolant entre quatre points.
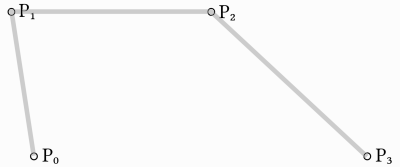
Nous utilisons d'abord une fonction à quatre paramètres pour prendre quatre points en entrée, p0, p1, p2 et p3 :
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
}
Nous appliquons une interpolation linéaire à chaque couple de points pour les réduire à trois :
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Nous prenons alors nos trois points et les réduisons à deux :
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Et à un :
var s = r0.lerp(r1, t)
return s
Vector2 s = r0.Lerp(r1, t);
return s;
Voici la fonction complète :
func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)
var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)
var s = r0.lerp(r1, t)
return s
private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);
Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);
Vector2 s = r0.Lerp(r1, t);
return s;
}
Le résultat sera une courbe lisse interpolant entre les quatre points :
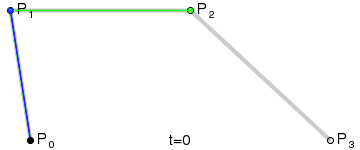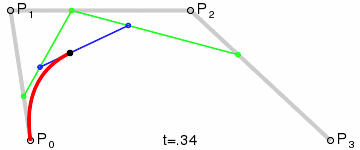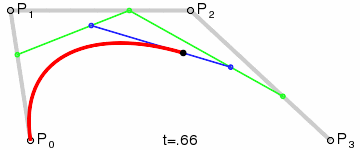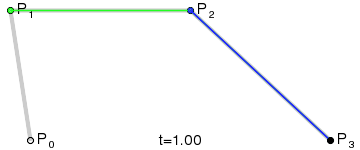
(Crédit image : Wikipedia)
Note
L'interpolation Bezier cubique fonctionne de la même façon en 3D, il suffit d'utiliser Vector3 au lieu de Vector2.
Ajout de points de contrôle¶
En nous basant sur Bézier cubique, nous pouvons changer la façon dont deux des points fonctionnent pour contrôler librement la forme de notre courbe. Au lieu d'avoir p0, p1, p2 et p3, nous allons les stocker comme :
point0 = p0: C'est le premier point, la sourcecontrol0 = p1 - p0: Est un vecteur relatif au premier point de contrôlecontrol1 = p3 - p2: Est un vecteur relatif au deuxième point de contrôlepoint1 = p3: C'est le deuxième point, la destination
De cette façon, nous avons deux points et deux points de contrôle qui sont des vecteurs relatifs aux points respectifs. Si vous avez déjà utilisé un logiciel de graphisme ou d'animation, cela peut vous sembler familier :
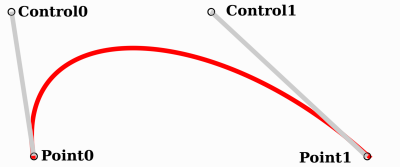
C'est ainsi que les logiciels graphiques présentent les courbes de Bézier aux utilisateurs, et comment elles fonctionnent et se présentent dans Godot.
Curve2D, Curve3D, Path et Path2D¶
Il y a deux objets qui contiennent des courbes : Curve3D et Curve2D (pour 3D et 2D respectivement).
They can contain several points, allowing for longer paths. It is also possible to set them to nodes: Path3D and Path2D (also for 3D and 2D respectively):
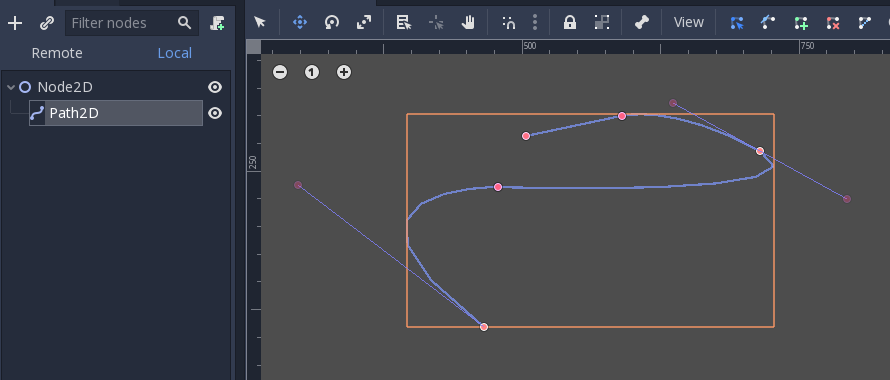
Cependant, leur utilisation n'est pas toujours évidente. Voici donc une description des cas d'utilisation les plus courants pour les courbes de Bézier.
Évaluer¶
Only evaluating them may be an option, but in most cases it's not very useful. The big drawback with Bezier curves is that if you traverse them at constant speed, from t = 0 to t = 1, the actual interpolation will not move at constant speed. The speed is also an interpolation between the distances between points p0, p1, p2 and p3 and there is not a mathematically simple way to traverse the curve at constant speed.
Let's do an example with the following pseudocode:
var t = 0.0
func _process(delta):
t += delta
position = _cubic_bezier(p0, p1, p2, p3, t)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = CubicBezier(p0, p1, p2, p3, _t);
}

Comme vous pouvez le voir, la vitesse (en pixels par seconde) du cercle varie, même si t est augmenté à vitesse constante. Cela rend les Béziers difficiles à utiliser dans la pratique de but en blanc.
Dessin¶
Dessiner des Béziers (ou objets basés sur la courbe) est un cas d'utilisation très courant, mais ce n'est pas facile non plus. Pour presque tous les cas, les courbes de Bézier doivent être converties en sorte de segments. Cependant, cela est normalement difficile, sans en créer un très grand nombre.
La raison en est que certaines sections d'une courbe (en particulier les coins) peuvent nécessiter un nombre considérable de points, alors que d'autres sections peuvent ne pas en nécessiter :

De plus, si les deux points de contrôle étaient 0, 0 (rappelez-vous que ce sont des vecteurs relatifs), la courbe de Bézier ne serait qu'une ligne droite (donc dessiner un grand nombre de points serait un gaspillage).
Avant de tracer les courbes de Bézier, une tesselation est nécessaire. Ceci est souvent fait avec une fonction récursive ou une fonction diviser pour régner qui divise la courbe jusqu'à ce que la valeur de courbure devienne inférieure à un certain seuil.
Les classes Curve fournissent ceci via la fonction Curve2D.tessellate() (qui reçoit les arguments optionnels stages de récursion et angle tolerance). De cette façon, il est plus facile de dessiner quelque chose à partir d'une courbe.
Parcourir¶
Le dernier cas d'utilisation courant pour les courbes est de les parcourir. En raison de ce qui a été mentionné précédemment concernant la vitesse constante, c'est également difficile.
To make this easier, the curves need to be baked into equidistant points. This way, they can be approximated with regular interpolation (which can be improved further with a cubic option). To do this, just use the Curve3D.sample_baked() method together with Curve2D.get_baked_length(). The first call to either of them will bake the curve internally.
Le parcours à vitesse constante peut donc être effectué avec le pseudo-code suivant :
var t = 0.0
func _process(delta):
t += delta
position = curve.sample_baked(t * curve.get_baked_length(), true)
private float _t = 0.0f;
public override void _Process(double delta)
{
_t += (float)delta;
Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}
Et la sortie se déplacera alors à une vitesse constante :
