Attention: Here be dragons

This is the latest (unstable) version of this documentation, which may document features not available in or compatible with released stable versions of Godot.

Checking the stable version of the documentation...

Matemáticas vectoriales¶

Introducción¶

Este tutorial es una breve y práctica introducción al álgebra lineal aplicada al desarrollo de juegos. El álgebra lineal es el estudio de los vectores y sus usos. Los vectores tienen muchas aplicaciones tanto en el desarrollo 2D como 3D y Godot los utiliza ampliamente. Desarrollar una buena comprensión de las matemáticas vectoriales es esencial para convertirse en un desarrollador de juegos sólido.

Nota

Este tutorial no es un libro de texto formal sobre álgebra lineal. Sólo veremos cómo se aplica al desarrollo de juegos. Para una visión más amplia de las matemáticas, consulta https://es.khanacademy.org/math/linear-algebra

Sistemas de coordenadas (2D)¶

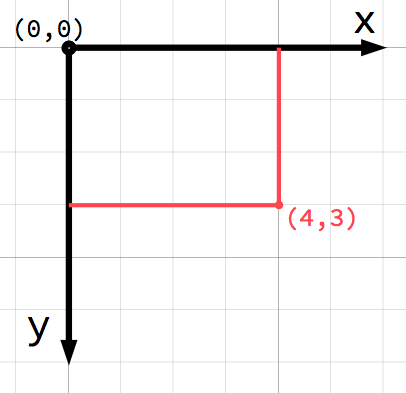
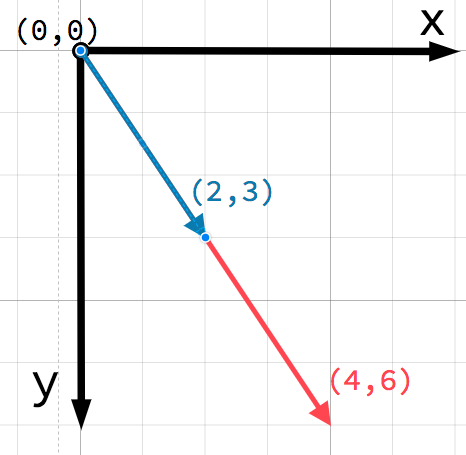
En el espacio 2D, las coordenadas se definen usando un eje horizontal (x) y un eje vertical (y). Una posición concreta en un espacio 2D se escribe como un par de valores como (4, 3).

Nota

Si eres nuevo en el mundo de los gráficos por computadora, puede parecer extraño que el eje positivo y apunte hacia abajo en lugar de hacia arriba, como probablemente aprendiste en la clase de matemáticas. Sin embargo, esto es común en la mayoría de las aplicaciones de gráficos por computadora.

Cualquier posición en el plano 2D puede ser identificada por un par de números de esta manera. Sin embargo, también podemos pensar en la posición (4, 3) como una compensación del punto (0, 0), u origen. Dibuja una flecha apuntando desde el origen hasta el punto:

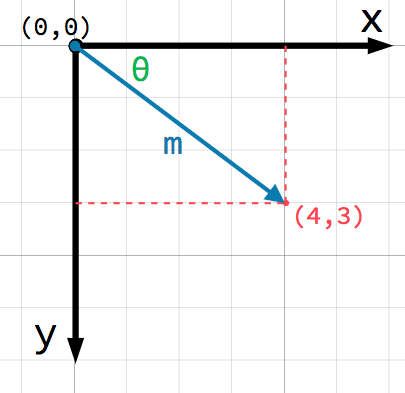
This is a vector. A vector represents a lot of useful information. As well as telling us that the point is at (4, 3), we can also think of it as an angle θ (theta) and a length (or magnitude) m. In this case, the arrow is a position vector - it denotes a position in space, relative to the origin.

Un punto muy importante a considerar acerca de los vectores es que ellos sólo representan dirección y magnitud relativa. No hay concepto de posición en un vector. Los siguientes dos vectores son idénticos:

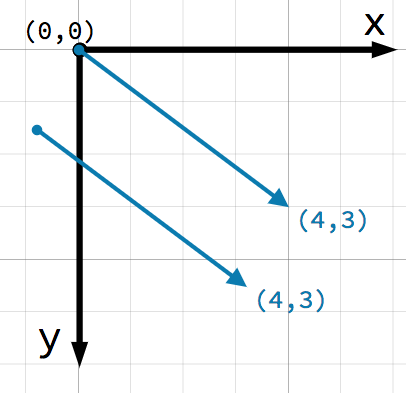
Ambos vectores representan un punto 4 unidades a la derecha y 3 unidades por debajo de algún punto de partida. No importa donde dibujes el vector en el plano, siempre representa una dirección y magnitud relativa.

Operaciones vectoriales¶

Se puede utilizar cualquiera de los dos métodos (coordenadas x e y o ángulo y magnitud) para referirse a un vector, pero por conveniencia los programadores típicamente usan la notación de coordenadas. Por ejemplo, en Godot el origen es la esquina superior izquierda de la pantalla, así que para colocar un nodo 2D llamado Node2D 400 píxeles a la derecha y 300 píxeles hacia abajo, usa el siguiente código:

$Node2D.position = Vector2(400, 300)

var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);

Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules discussed in this article apply to both types, and wherever we link to Vector2 methods in the class reference, you can also check out their Vector3 counterparts.

Acceso para miembros¶

Se puede acceder directamente a los componentes individuales del vector por nombre.

# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1

// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;

Añadir vectores¶

Al sumar o restar dos vectores, se suman los componentes correspondientes:

var c = a + b  # (2, 5) + (3, 1) = (5, 6)

var c = a + b;  // (2, 5) + (3, 1) = (5, 6)

También podemos ver esto visualmente añadiendo el segundo vector al final del primero:

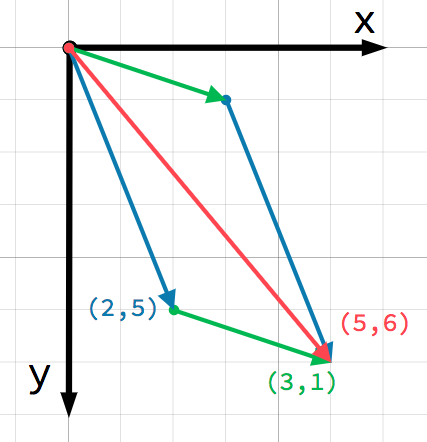
Nota que sumar a + b da el mismo resultado que b + a.

Multiplicación escalar¶

Nota

Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.

Un vector puede ser multiplicado por un escalar:

var c = a * 2  # (2, 5) * 2 = (4, 10)
var d = b / 3  # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)

var c = a * 2;  // (2, 5) * 2 = (4, 10)
var d = b / 3;  // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)

Nota

Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.

Aplicaciones prácticas¶

Veamos dos usos comunes para sumar y restar vectores.

Movimiento¶

A vector can represent any quantity with a magnitude and direction. Typical examples are: position, velocity, acceleration, and force. In this image, the spaceship at step 1 has a position vector of (1, 3) and a velocity vector of (2, 1). The velocity vector represents how far the ship moves each step. We can find the position for step 2 by adding the velocity to the current position.

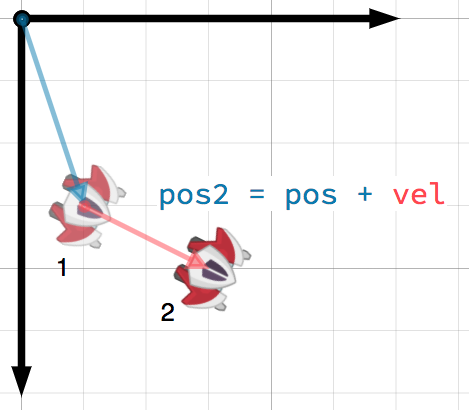
Truco

Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.

In a typical 2D game scenario, you would have a velocity in pixels per second, and multiply it by the delta parameter (time elapsed since the previous frame) from the _process() or _physics_process() callbacks.

Apuntar hacia un objetivo¶

En este escenario, hay un tanque que desea apuntar con su torreta a un robot. Si se resta la posición del tanque de la posición del robot, el vector apunta desde el tanque al robot.

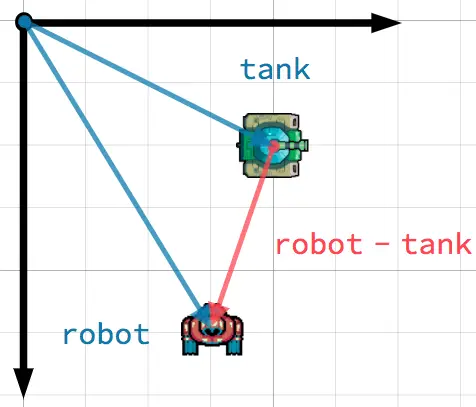
Truco

To find a vector pointing from A to B, use B - A.

Vectores unitarios¶

Un vector con magnitud de 1 se llama vector unitario. También se les conoce como vectores de dirección o normales. Los vectores unitarios son útiles cuando se necesita llevar un registro de una dirección.

Normalización¶

Normalizing a vector means reducing its length to 1 while preserving its direction. This is done by dividing each of its components by its magnitude. Because this is such a common operation, Godot provides a dedicated normalized() method for this:

a = a.normalized()

a = a.Normalized();

Advertencia

Because normalization involves dividing by the vector's length, you cannot normalize a vector of length 0. Attempting to do so would normally result in an error. In GDScript though, trying to call the normalized() method on a vector of length 0 leaves the value untouched and avoids the error for you.

Reflexión¶

Un uso común de los vectores unitarios es indicar normales. Los vectores normales son vectores unitarios alineados perpendicularmente a una superficie, definiendo su dirección. Se utilizan comúnmente para iluminación, colisiones y otras operaciones que involucran superficies.

Por ejemplo, imagina que tenemos una pelota en movimiento que queremos rebotar en una pared u otro objeto:

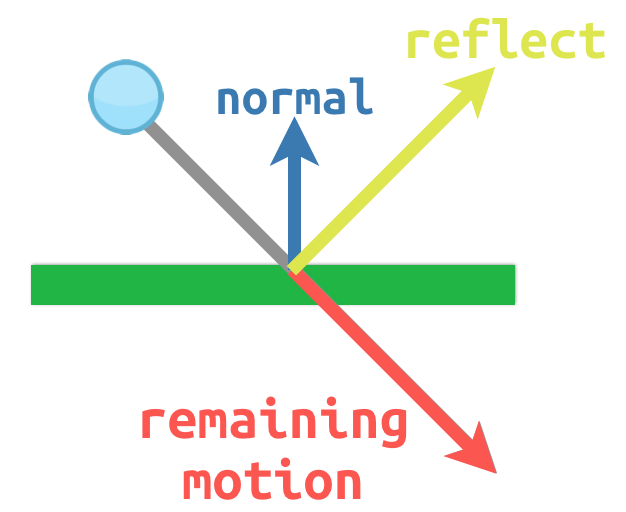
The surface normal has a value of (0, -1) because this is a horizontal surface. When the ball collides, we take its remaining motion (the amount left over when it hits the surface) and reflect it using the normal. In Godot, there is a bounce() method to handle this. Here is a code example of the above diagram using a CharacterBody2D:

var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
    var reflect = collision.get_remainder().bounce(collision.get_normal())
    velocity = velocity.bounce(collision.get_normal())
    move_and_collide(reflect)

KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
    var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
    _velocity = _velocity.Bounce(collision.GetNormal());
    MoveAndCollide(reflect);
}

Producto punto¶

El producto punto es uno de los conceptos más importantes en la matemática vectorial, pero a menudo es malentendido. El producto punto es una operación en dos vectores que devuelve un escalar. A diferencia de un vector, que contiene tanto la magnitud como la dirección, un valor escalar sólo tiene magnitud.

La fórmula para el producto punto toma dos formas comunes:

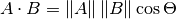
y

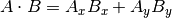
The mathematical notation ||A|| represents the magnitude of vector A, and A_x means the x component of vector A.

However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:

var c = a.dot(b)
var d = b.dot(a)  # These are equivalent.

float c = a.Dot(b);
float d = b.Dot(a);  // These are equivalent.

The dot product is most useful when used with unit vectors, making the first formula reduce to just cos(θ). This means we can use the dot product to tell us something about the angle between two vectors:

Cuando se utilizan vectores unitarios, el resultado estará siempre entre -1 (180°) y 1 (0°).

Orientación¶

Podemos usar este hecho para detectar si un objeto está orientado hacia otro objeto. En el diagrama de abajo, el jugador P está tratando de evitar a los zombis A y B. Asumiendo que el campo de visión de un zombi es 180°, ¿pueden ver al jugador?

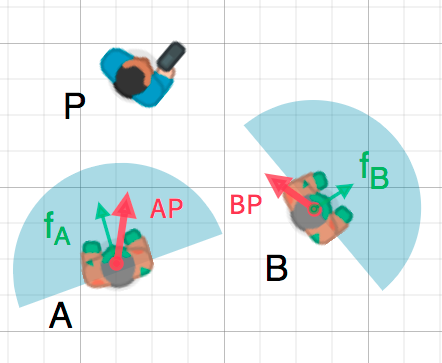
The green arrows fA and fB are unit vectors representing the zombie's facing direction and the blue semicircle represents its field of view. For zombie A, we find the direction vector AP pointing to the player using P - A and normalize it, however, Godot has a helper method to do this called direction_to(). If the angle between this vector and the facing vector is less than 90°, then the zombie can see the player.

En código se vería así:

var AP = A.direction_to(P)
if AP.dot(fA) > 0:
    print("A sees P!")

var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
    GD.Print("A sees P!");
}

Producto vectorial¶

Al igual que el producto punto, el producto vectorial (o producto cruz) es una operación sobre dos vectores. Sin embargo, el resultado del producto vectorial es un vector con una dirección que es perpendicular a ambos. Su magnitud depende de su ángulo relativo. Si dos vectores son paralelos, el resultado de su producto cruz será nulo.

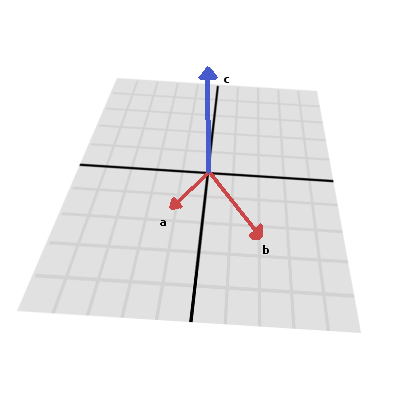
El producto vectorial se calcula así:

var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)

var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);

With Godot, you can use the built-in Vector3.cross() method:

var c = a.cross(b)

var c = a.Cross(b);

The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.

Nota

En el producto vectorial, el orden importa. a.cross(b) no da el mismo resultado que b.cross(a). Los vectores resultantes apuntan en direcciones opuestas.

Calculando normales¶

One common use of cross products is to find the surface normal of a plane or surface in 3D space. If we have the triangle ABC we can use vector subtraction to find two edges AB and AC. Using the cross product, AB × AC produces a vector perpendicular to both: the surface normal.

A continuación se muestra una función para calcular el normal en un triángulo:

func get_triangle_normal(a, b, c):
    # Find the surface normal given 3 vertices.
    var side1 = b - a
    var side2 = c - a
    var normal = side1.cross(side2)
    return normal

Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
    // Find the surface normal given 3 vertices.
    var side1 = b - a;
    var side2 = c - a;
    var normal = side1.Cross(side2);
    return normal;
}

Apuntando a un objetivo¶

En la sección de producto punto anterior, vimos cómo se podía usar para encontrar el ángulo entre dos vectores. Sin embargo, en 3D esto no es suficiente información. También necesitamos saber qué eje girar. A esto podemos encontrarlo calculando el producto vectorial de la dirección de orientación actual y la dirección objetivo. El vector perpendicular resultante es el eje de rotación.

Más información¶

Para más información sobre el uso de la matemática vectorial en Godot, consulta los siguientes artículos: