Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
高等向量数学¶
平面¶
单位向量的点积还有一个有趣的性质。请想象垂直于这个向量(通过原点)经过一个平面。平面将整个空间划分为正(在平面上)和负(在平面下),而(与普遍的看法相反)你也可以在 2D 中进行这样的数学运算:
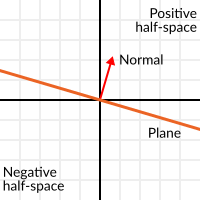
垂直于表面的单位向量称为单位法向量(因此,它们描述的是表面的朝向)。不过,通常会把它们缩写为法线。平面、3D 几何体等场合中都会用到法线(用来确定各个面或顶点的侧边)。法线是一种单位向量,因为用途才被称为法线。(就像我们说坐标 (0,0) 是“原点”一样!)。
The plane passes by the origin and the surface of it is perpendicular to the unit vector (or normal). The side towards the vector points to is the positive half-space, while the other side is the negative half-space. In 3D this is exactly the same, except that the plane is an infinite surface (imagine an infinite, flat sheet of paper that you can orient and is pinned to the origin) instead of a line.
到平面的距离¶
现在平面是什么就很清楚了,让我们再回到点积上。单位向量和任何空间点之间的点积(是的,这次我们在向量和位置之间进行点乘),将返回从该点到平面的距离:
var distance = normal.dot(point)
var distance = normal.Dot(point);
但不仅仅是绝对距离, 如果点在负半空间中, 距离也是负的:
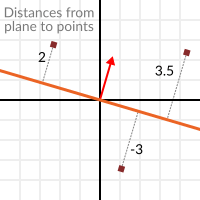
这使我们能够知道点在平面的哪一侧.
远离原点¶
我知道你在想什么!到目前为止, 这还不错, 但 真正的 平面在空间中无处不在, 而不仅仅是通过原点的平面. 你想要真正的 平面 , 你 现在 就想行动起来.
记住, 平面不仅把空间分成两半, 而且它们还有 极性 . 这意味着有可能有完全重叠的平面, 但是它们的负半空间和正半空间是相反的.
记住这一点, 让我们将整个平面描述为 法线 N 和 距原点的距离 标量 D . 因此, 我们的平面将由N和D表示, 例如:
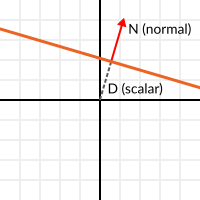
对于3维的情况,Godot提供了一个 Plane 内置类型来处理这个问题.
基本上,N和D可以表示空间中的任何平面, 无论是对于2D还是3D(取决于变量N的维数), 数学上对于两者都是一样的. 和以前差不多, 但D是原点沿N方向移动到平面的距离. 例如, 想象一下你想在到达平面上的一个点, 你会这样做:
var point_in_plane = N*D
var pointInPlane = N * D;
这将拉伸(调整大小)法线向量并使其接触平面. 这个数学可能看起来很疑惑, 但实际上比看起来简单得多. 如果我们想再说一遍, 从点到平面的距离, 我们也会这样做, 但是要调整距离:
var distance = N.dot(point) - D
var distance = N.Dot(point) - D;
使用内置函数做同样的事情:
var distance = plane.distance_to(point)
var distance = plane.DistanceTo(point);
这将再次返回一个正或负的距离.
翻转平面的极性可以通过同时对N和D取负来完成. 这将导致平面处于相同的位置, 但是具有反转的负半空间和正半空间:
N = -N
D = -D
N = -N;
D = -D;
Godot also implements this operator in Plane. So, using the format below will work as expected:
var inverted_plane = -plane
var invertedPlane = -plane;
So, remember, the plane's main practical use is that we can calculate the distance to it. So, when is it useful to calculate the distance from a point to a plane? Let's see some examples.
在二维空间中构造平面¶
平面显然不是从哪儿冒出来的, 所以必须构造. 在2D中构造它们很简单, 这可以从法线(单位向量)和点, 或者用2维空间中的两个点来完成.
In the case of a normal and a point, most of the work is done, as the normal is already computed, so calculate D from the dot product of the normal and the point.
var N = normal
var D = normal.dot(point)
var N = normal;
var D = normal.Dot(point);
对于空间中的两个点, 实际上会有两个平面同时经过它们, 它们共享相同的空间, 但是法线方向相反. 为了从这两个点计算面的法线, 必须首先获得方向向量, 然后将向任何一边旋转90°:
# Calculate vector from `a` to `b`.
var dvec = point_a.direction_to(point_b)
# Rotate 90 degrees.
var normal = Vector2(dvec.y, -dvec.x)
# Alternatively (depending the desired side of the normal):
# var normal = Vector2(-dvec.y, dvec.x)
// Calculate vector from `a` to `b`.
var dvec = pointA.DirectionTo(pointB);
// Rotate 90 degrees.
var normal = new Vector2(dvec.Y, -dvec.X);
// Alternatively (depending the desired side of the normal):
// var normal = new Vector2(-dvec.Y, dvec.X);
The rest is the same as the previous example. Either point_a or point_b will work, as they are in the same plane:
var N = normal
var D = normal.dot(point_a)
# this works the same
# var D = normal.dot(point_b)
var N = normal;
var D = normal.Dot(pointA);
// this works the same
// var D = normal.Dot(pointB);
Doing the same in 3D is a little more complex and is explained further down.
平面的一些示例¶
Here is an example of what planes are useful for. Imagine you have a convex polygon. For example, a rectangle, a trapezoid, a triangle, or just any polygon where no faces bend inwards.
对多边形的每个部分, 我们计算出经过该部分的平面. 一旦我们有了平面的列表, 我们就可以做些分类的事情, 例如检查一个点是否在多边形内部.
我们遍历所有平面, 如果我们能找到使得点到平面的距离为正的平面, 那么点在多边形之外. 如果我们不能, 那么这一点就在多边形内部.
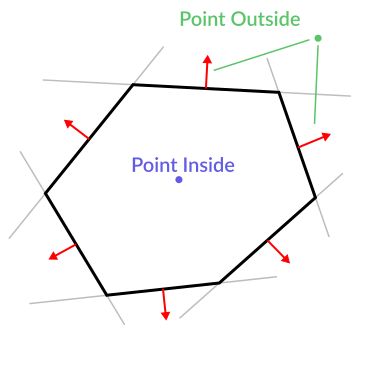
代码应该是这样的:
var inside = true
for p in planes:
# check if distance to plane is positive
if (p.distance_to(point) > 0):
inside = false
break # with one that fails, it's enough
var inside = true;
foreach (var p in planes)
{
// check if distance to plane is positive
if (p.DistanceTo(point) > 0)
{
inside = false;
break; // with one that fails, it's enough
}
}
很酷, 是吧?但这可以变得更好!稍加努力, 类似的逻辑将让我们知道两个凸多边形是否重叠. 这叫做分离轴定理(或SAT), 大多数物理引擎都用这个来检测碰撞.
对于一个点, 仅仅检查一个平面是否返回正距离就足以判断该点是否在外面. 对于一个多边形, 我们必须找到一个平面, 使得另一个多边形上的所有点到它的距离为正. 这种可以用A平面对B点进行检查, 然后用B平面对A点进行检查:

代码应该是这样的:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
print("Polygons Collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
正如你所看到的, 平面是非常有用的, 然而这只是冰山一角. 你可能想知道非凸多边形会发生什么. 这通常只是通过将凹多边形分割成较小的凸多边形来处理, 或者使用诸如BSP(现在使用得不多)之类的技术.
三维碰撞检测¶
这是另一个奖励, 是对耐心并跟上这个漫长的教程的奖励. 这是另一条锦囊妙计. 这可能不能直接拿来使用(Godot已经可以进行了相当棒的碰撞检测了), 但是几乎所有的物理引擎和碰撞检测库都使用它的原理:)
还记得把2D中的凸形转换成2D平面阵列对碰撞检测有用吗?你可以检测一个点是否在任何凸形状内, 或者两个2D凸形状是否重叠.
嗯, 这在3D中也适用, 如果两个3D多面体形状碰撞, 你将无法找到分离平面. 如果发现一个分离平面, 那么形状肯定不会发生碰撞.
要得到分离平面意味着多边形A的所有顶点都在平面的一侧, 而多边形B的所有顶点都在另一侧. 该平面始终是多边形A或多边形B的面向平面之一.
然而在3D中, 这种方法存在一个问题, 因为在某些情况下可能找不到分离平面. 下面就是这种情况的一个示例:

为了避免这种情况,一些额外的平面需要作为分隔器被测试,这些平面是多边形 A 的边和多边形 B 的边的叉积
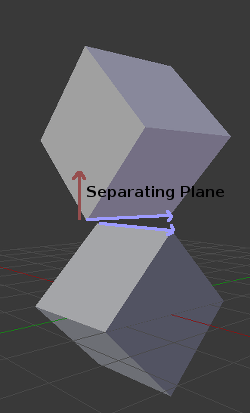
所以最后的算法是这样的:
var overlapping = true
for p in planes_of_A:
var all_out = true
for v in points_of_B:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
# a separating plane was found
# do not continue testing
overlapping = false
break
if (overlapping):
# only do this check if no separating plane
# was found in planes of A
for p in planes_of_B:
var all_out = true
for v in points_of_A:
if (p.distance_to(v) < 0):
all_out = false
break
if (all_out):
overlapping = false
break
if (overlapping):
for ea in edges_of_A:
for eb in edges_of_B:
var n = ea.cross(eb)
if (n.length() == 0):
continue
var max_A = -1e20 # tiny number
var min_A = 1e20 # huge number
# we are using the dot product directly
# so we can map a maximum and minimum range
# for each polygon, then check if they
# overlap.
for v in points_of_A:
var d = n.dot(v)
max_A = max(max_A, d)
min_A = min(min_A, d)
var max_B = -1e20 # tiny number
var min_B = 1e20 # huge number
for v in points_of_B:
var d = n.dot(v)
max_B = max(max_B, d)
min_B = min(min_B, d)
if (min_A > max_B or min_B > max_A):
# not overlapping!
overlapping = false
break
if (not overlapping):
break
if (overlapping):
print("Polygons collided!")
var overlapping = true;
foreach (Plane plane in planesOfA)
{
var allOut = true;
foreach (Vector3 point in pointsOfB)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
// a separating plane was found
// do not continue testing
overlapping = false;
break;
}
}
if (overlapping)
{
// only do this check if no separating plane
// was found in planes of A
foreach (Plane plane in planesOfB)
{
var allOut = true;
foreach (Vector3 point in pointsOfA)
{
if (plane.DistanceTo(point) < 0)
{
allOut = false;
break;
}
}
if (allOut)
{
overlapping = false;
break;
}
}
}
if (overlapping)
{
foreach (Vector3 edgeA in edgesOfA)
{
foreach (Vector3 edgeB in edgesOfB)
{
var normal = edgeA.Cross(edgeB);
if (normal.Length() == 0)
{
continue;
}
var maxA = float.MinValue; // tiny number
var minA = float.MaxValue; // huge number
// we are using the dot product directly
// so we can map a maximum and minimum range
// for each polygon, then check if they
// overlap.
foreach (Vector3 point in pointsOfA)
{
var distance = normal.Dot(point);
maxA = Mathf.Max(maxA, distance);
minA = Mathf.Min(minA, distance);
}
var maxB = float.MinValue; // tiny number
var minB = float.MaxValue; // huge number
foreach (Vector3 point in pointsOfB)
{
var distance = normal.Dot(point);
maxB = Mathf.Max(maxB, distance);
minB = Mathf.Min(minB, distance);
}
if (minA > maxB || minB > maxA)
{
// not overlapping!
overlapping = false;
break;
}
}
if (!overlapping)
{
break;
}
}
}
if (overlapping)
{
GD.Print("Polygons Collided!");
}
更多信息¶
关于在Godot中使用向量数学的更多信息, 请参见以下文章:
如果你需要进一步的解释,你可以看看 3Blue1Brown 的绝佳的系列视频《线性代数的本质》:http://www.bilibili.com/video/BV1ys411472E?p=2