Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Векторная математика¶
Введение¶
Этот урок - короткое и практичное введение в линейную алгебру, применяемую в разработке игр. Линейная алгебра изучает векторы и их использование. Векторы могут применяться в 2D и 3D разработке и Godot использует их интенсивно. Разработчику игр требуется хорошее понимание векторной алгебры чтобы стать сильным в этой области.
Примечание
Этот урок — не учебник по линейной алгебре. Мы рассмотрим только то, что применяется в разработке игр. Для более широкого взгляда на математику, смотрите https://www.khanacademy.org/math/linear-algebra
Системы координат (2D)¶
В 2D пространстве, координаты определены использованием горизонтальной оси (x) и вертикальной оси (y). Определённая позиция в 2D пространстве записывается как пара значений, таких как (4, 3).
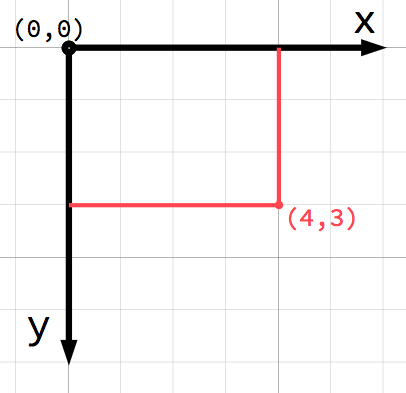
Примечание
Если вы новичок в компьютерной графике, вам может показаться странным, что положительная ось y указывает вниз, а не вверх, как вас учили в школе. Тем не менее, в приложениях компьютерной графики это встречается повсеместно.
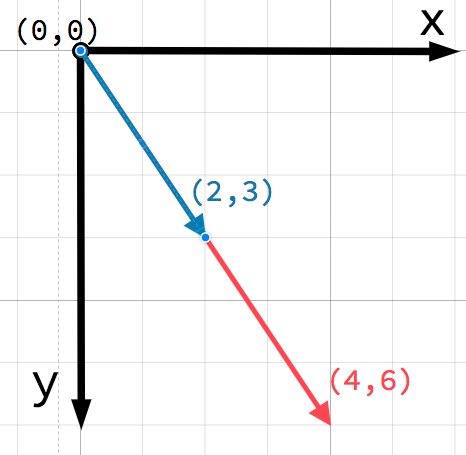
Любая точка на 2D плоскости может быть таким образом определена парой чисел. Вы также можете рассматривать (4, 3) как смещение от точки (0, 0), или точки начала координат. Нарисуем стрелку от начала координат до заданной точки:
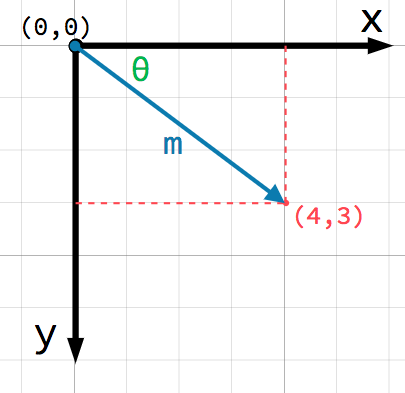
Это вектор. Вектор предоставляет множество полезной информации. Помимо сообщения нам, что точка расположена в (4, 3), мы можем также представить это в виде угла θ и длины (величины, модуля) m. В данном примере стрелка — это вектор позиции — он обозначает позицию в пространстве относительно начала координат.
При рассмотрении векторов крайне важно иметь в виду, что они представляют только относительные направление и величину (модуль). Вектору нельзя приписать определённой позиции. Два следующих вектора идентичны:
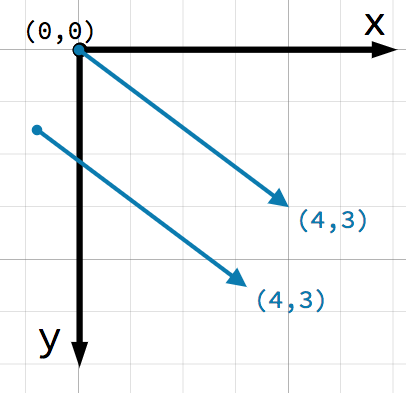
Оба вектора представляют точку 4 единицами правее и 3 единицами ниже стартовой точки. Неважно, где на плоскости вы нарисуете вектор, он всегда представляет относительное направление и величину.
Операции над векторами¶
Вы можете применять любой из методов (задание координат x и y или угла с длиной) для определения вектора, но обычно программисты используют координаты. Для примера, в Godot начало координат — это верхний-левый угол экрана, так что для перемещения 2D узла с именем Node2D на 400 пикселей вправо и 300 вниз используйте следующий код:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot поддерживает типы Vector2 и Vector3 для 2D и 3D соответственно. Математические правила, рассказанные в этой статье, применяются к обоим типам, и везде, где мы ссылаемся на методы Vector2 в ссылке на класс, вы также можете ознакомиться с их аналогами Vector3.
Доступ к полям¶
К отдельным компонентам вектора можно обращаться непосредственно по имени.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Сложение векторов¶
Когда два вектора складываются или вычитаются, складываются соответствующие компоненты:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
Мы также можем посмотреть визуально на добавление второго вектора к концу первого:
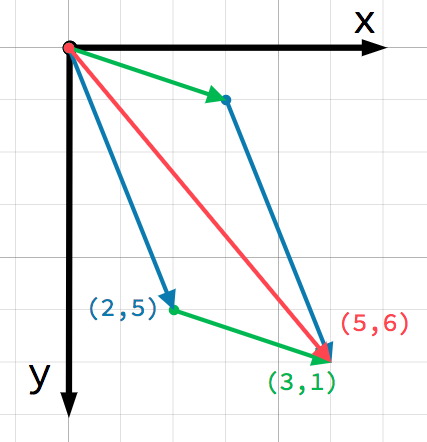
Отметьте что сложение a + b даёт такой же результат что и b + a.
Скалярное перемножение¶
Примечание
Векторы представляют как направление, так и величину. Значение, представляющее только величину, называется скаляром. в Godot, скаляры используют тип float.
Вектор может быть умножен на скаляр:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Примечание
Умножение вектора на положительный скаляр не изменяет его направление, а только величину. Умножение на отрицательный скаляр приводит к получению вектора в противоположном направлении. Вот как вы масштабируете вектор.
Практические применения¶
Давайте посмотрим на два обычных приёма использования для векторного сложения и вычитания.
Движение¶
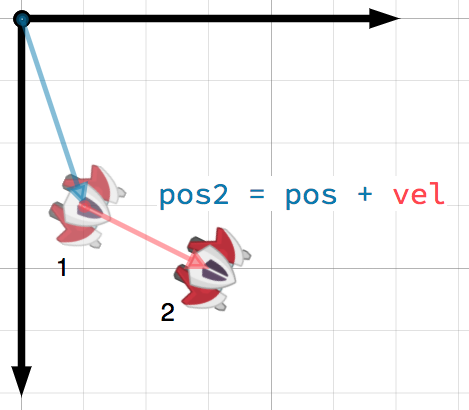
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
Совет
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
Направление в сторону цели¶
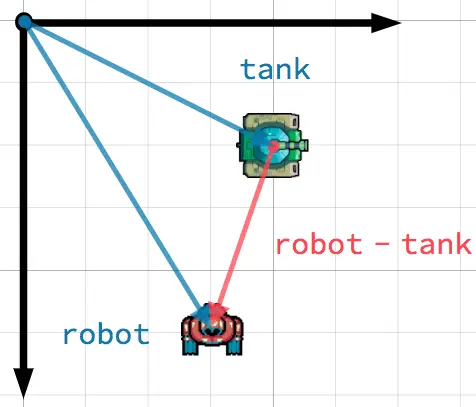
В этом примере вы, управляя танком, хотите направить дуло на робота. Вычитание позиции танка из позиции робота даёт вектор, направленный от танка к роботу.
Совет
To find a vector pointing from A to B, use B - A.
Единичные векторы¶
Вектор с длиной, равной 1, называется единичным вектором. Они также иногда называются векторами направления или нормалями. Единичные векторы полезны, когда вам нужно сохранить направление без учёта длины.
Нормализация¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
Предупреждение
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
Отражение¶
Обычный пример использования единичных векторов - определение нормалей. Векторы нормалей - это единичные векторы, перпендикулярные к поверхности, определяющей их направление. Обычно они используются в обработке света, столкновений и других операциях с поверхностями.
Например, представьте что вы движете шар, который вы хотите отражать от стен или других объектов:
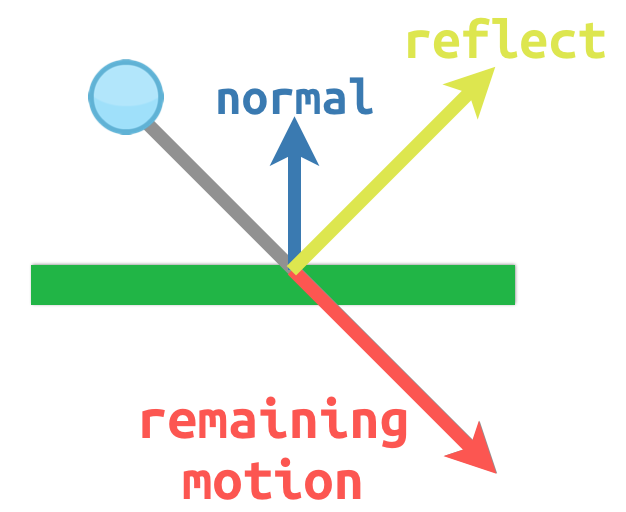
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Скалярное произведение¶
Результат скалярного произведения очень важный аспект в векторной алгебре, но его также часто плохо понимают. Скалярное произведение это операция над двумя векторами которая возвращает скаляр. В отличии от вектора, который содержит длину и направление, скаляр содержит только длину.
Формула скалярного произведения имеет две распространённых формы:
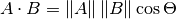
и
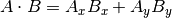
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
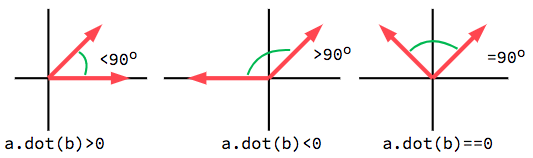
При использовании единичных векторов результат всегда будет находиться между -1 (180°) и 1 (0°).
Направление взгляда¶
Мы можем использовать этот факт для обнаружения, что объект смотрит в направлении другого объекта. На диаграмме ниже, игрок P пытается избежать взгляда зомби A и B. Могут ли зомби его увидеть если их угол обзора равен 180° ?
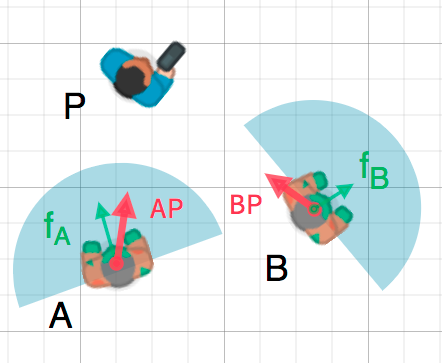
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
В коде это бы выглядело как:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Векторное произведение¶
Также как и скалярное произведение, векторное произведение это операция над двумя векторами. Но в результате векторного произведения вы получаете вектор с направлением перпендикулярным обоим исходным векторам. Его длина зависит от их относительного угла. Если два вектора параллельны, в результате вы получите нулевой вектор.

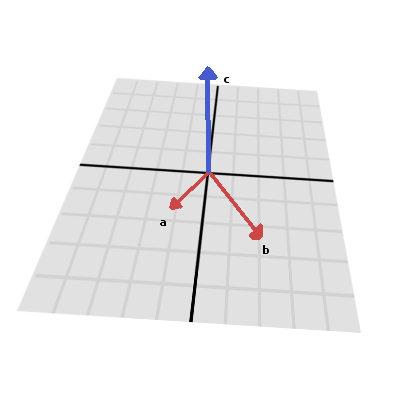
Векторное произведение вычисляется так:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
Примечание
В векторном произведении, порядок аргументов важен. a.cross(b) не даёт такого же результата что и b.cross(a). Получаемые векторы имеют противоположные направления.
Расчитывание нормалей¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
Здесь показана функция для вычисления нормали треугольника:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Направление на цель¶
В скалярном произведении выше, мы видели как оно может использоваться для нахождения угла между двумя векторами. Однако для 3D этого недостаточно. Мы также должны знать вокруг какой оси нужно осуществлять вращение. Мы можем найти её выполняя векторное произведение текущего направления взгляда и направлением цели. В результате мы получим перпендикулярный вектор оси вращения.
Дополнительная информация¶
Для большей информации об использовании векторной алгебры в Godot, смотрите следующие статьи: