Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Власне малювання в 2D¶
Вступ¶
Godot has nodes to draw sprites, polygons, particles, and all sorts of stuff. For most cases, this is enough. If there's no node to draw something specific you need, you can make any 2D node (for example, Control or Node2D based) draw custom commands.
Власне малювання в 2D вузлах дійсно корисне. Ось деякі випадки використання:
Малювання фігур, або логіки, які не можуть зробити існуючі вузли, наприклад, зображення зі слідами, або спеціальний анімований багатокутник.
Візуалізації, несумісні з вузлами, наприклад, дошка тетріса. (Для прикладу тетріс використовує спеціальну функцію малювання для малювання блоків.)
Малювання великої кількості простих об'єктів. Власне малюнок дозволяє уникнути використання великої кількості вузлів, можливо, знижуючи використання пам'яті та покращуючи продуктивність.
Створення власного елемента керування інтерфейсом користувача. Доступно багато елементів керування, але коли у вас є незвичайні потреби, вам, ймовірно, знадобиться власний контроль.
Малюнок¶
Додайте скрипт до будь-якого похідного вузла CanvasItem, наприклад Control, або Node2D. Потім перевизначте функцію _draw().
extends Node2D
func _draw():
# Your draw commands here
pass
public override void _Draw()
{
// Your draw commands here
}
Команди малювання описані в посиланні на клас CanvasItem. Їх багато.
Оновлення¶
Функція _draw() викликається тільки один раз, а потім команди малювання кешуються і запам'ятовуються, тому подальші виклики непотрібні.
If re-drawing is required because a state or something else changed,
call CanvasItem.queue_redraw()
in that same node and a new _draw() call will happen.
Ось трохи складніший приклад, змінна текстури, яка буде перемальована при зміні:
extends Node2D
@export var texture: Texture:
set = _set_texture
func _set_texture(value):
# If the texture variable is modified externally,
# this callback is called.
texture = value # Texture was changed.
queue_redraw() # Trigger a redraw of the node.
func _draw():
draw_texture(texture, Vector2())
using Godot;
public partial class MyNode2D : Node2D
{
private Texture _texture;
public Texture Texture
{
get
{
return _texture;
}
set
{
_texture = value;
QueueRedraw();
}
}
public override void _Draw()
{
DrawTexture(_texture, new Vector2());
}
}
In some cases, it may be desired to draw every frame. For this,
call queue_redraw() from the _process() callback, like this:
extends Node2D
func _draw():
# Your draw commands here
pass
func _process(delta):
queue_redraw()
using Godot;
public partial class CustomNode2D : Node2D
{
public override void _Draw()
{
// Your draw commands here
}
public override void _Process(double delta)
{
QueueRedraw();
}
}
Координати¶
The drawing API uses the CanvasItem's coordinate system, not necessarily pixel coordinates. Which means it uses the coordinate space created after applying the CanvasItem's transform. Additionally, you can apply a custom transform on top of it by using draw_set_transform or draw_set_transform_matrix.
When using draw_line, you should consider the width of the line.
When using a width that is an odd size, the position should be shifted
by 0.5 to keep the line centered as shown below.
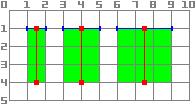
func _draw():
draw_line(Vector2(1.5, 1.0), Vector2(1.5, 4.0), Color.GREEN, 1.0)
draw_line(Vector2(4.0, 1.0), Vector2(4.0, 4.0), Color.GREEN, 2.0)
draw_line(Vector2(7.5, 1.0), Vector2(7.5, 4.0), Color.GREEN, 3.0)
public override void _Draw()
{
DrawLine(new Vector2(1.5f, 1.0f), new Vector2(1.5f, 4.0f), Colors.Green, 1.0f);
DrawLine(new Vector2(4.0f, 1.0f), new Vector2(4.0f, 4.0f), Colors.Green, 2.0f);
DrawLine(new Vector2(7.5f, 1.0f), new Vector2(7.5f, 4.0f), Colors.Green, 3.0f);
}
The same applies to the draw_rect method with filled = false.
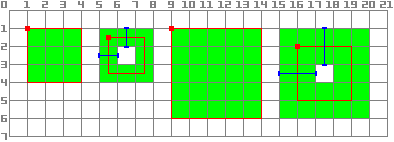
func _draw():
draw_rect(Rect2(1.0, 1.0, 3.0, 3.0), Color.GREEN)
draw_rect(Rect2(5.5, 1.5, 2.0, 2.0), Color.GREEN, false, 1.0)
draw_rect(Rect2(9.0, 1.0, 5.0, 5.0), Color.GREEN)
draw_rect(Rect2(16.0, 2.0, 3.0, 3.0), Color.GREEN, false, 2.0)
public override void _Draw()
{
DrawRect(new Rect2(1.0f, 1.0f, 3.0f, 3.0f), Colors.Green);
DrawRect(new Rect2(5.5f, 1.5f, 2.0f, 2.0f), Colors.Green, false, 1.0f);
DrawRect(new Rect2(9.0f, 1.0f, 5.0f, 5.0f), Colors.Green);
DrawRect(new Rect2(16.0f, 2.0f, 3.0f, 3.0f), Colors.Green, false, 2.0f);
}
Приклад: малювання кругових дуг¶
Тепер ми будемо використовувати спеціальну функціональність малювання Godot Engine, щоб намалювати те, для чого Godot не надає функцій. Як приклад, Godot надає функцію draw_circle(), яка малює ціле коло. Однак, як щодо малювання частини кола? Вам доведеться закодувати функцію, щоб виконати її і намалювати частину кола самостійно.
Функція дуги¶
Дуга визначається її параметрами опорного кола, тобто центральним положенням і радіусом. Сама дуга потім визначається кутом, з якого вона починається, і кутом, під яким вона зупиняється. Це 4 аргументи, які ми повинні надати нашій функції малювання. Ми також надамо значення кольору, щоб ми могли намалювати дугу в різних кольорах, якщо захочемо.
В основному, малювання фігури на екрані вимагає, щоб вона була розкладена на певну кількість точок, пов'язаних від однієї до іншої. Як розумієте, чим з більшої кількості точок складається ваша форма, тим гладкішою вона виглядає, але тим важча вона з точки зору обробки. Загалом, якщо ваша форма величезна (або в 3D, близько до камери), треба буде намалювати більше точок, щоб досягти гладкості. І навпаки, якщо ваша форма невелика (або в 3D, далеко від камери), ви можете зменшити кількість її точок, щоб заощадити витрати на обробку; це називається рівень деталізації (LOD). У нашому прикладі ми просто будемо використовувати фіксовану кількість точок, незалежно від радіуса.
func draw_circle_arc(center, radius, angle_from, angle_to, color):
var nb_points = 32
var points_arc = PackedVector2Array()
for i in range(nb_points + 1):
var angle_point = deg_to_rad(angle_from + i * (angle_to-angle_from) / nb_points - 90)
points_arc.push_back(center + Vector2(cos(angle_point), sin(angle_point)) * radius)
for index_point in range(nb_points):
draw_line(points_arc[index_point], points_arc[index_point + 1], color)
public void DrawCircleArc(Vector2 center, float radius, float angleFrom, float angleTo, Color color)
{
int nbPoints = 32;
var pointsArc = new Vector2[nbPoints + 1];
for (int i = 0; i <= nbPoints; i++)
{
float anglePoint = Mathf.DegToRad(angleFrom + i * (angleTo - angleFrom) / nbPoints - 90f);
pointsArc[i] = center + new Vector2(Mathf.Cos(anglePoint), Mathf.Sin(anglePoint)) * radius;
}
for (int i = 0; i < nbPoints - 1; i++)
{
DrawLine(pointsArc[i], pointsArc[i + 1], color);
}
}
Remember the number of points our shape has to be decomposed into? We fixed this
number in the nb_points variable to a value of 32. Then, we initialize an empty
PackedVector2Array, which is simply an array of Vector2s.
Наступний крок складається з обчислення фактичних позицій цих 32 точок, які складають дугу. Це робиться в першому циклі for: ми ітеруємо кількість точок, для яких хочемо обчислити позиції, плюс одну, щоб включити останню точку. Спочатку визначаємо кут кожної точки, між початковим і кінцевим кутами.
The reason why each angle is decreased by 90° is that we will compute 2D positions
out of each angle using trigonometry (you know, cosine and sine stuff...). However,
cos() and sin() use radians, not degrees. The angle of 0° (0 radian)
starts at 3 o'clock, although we want to start counting at 12 o'clock. So we decrease
each angle by 90° in order to start counting from 12 o'clock.
The actual position of a point located on a circle at angle angle (in radians)
is given by Vector2(cos(angle), sin(angle)). Since cos() and sin() return values
between -1 and 1, the position is located on a circle of radius 1. To have this
position on our support circle, which has a radius of radius, we simply need to
multiply the position by radius. Finally, we need to position our support circle
at the center position, which is performed by adding it to our Vector2 value.
Finally, we insert the point in the PackedVector2Array which was previously defined.
Тепер ми повинні дійсно намалювати наші точки. Як ви можете здогадатися, ми не просто намалюємо наші 32 точки: нам потрібно намалювати все, що є між кожною з них. Ми могли б обчислити кожну точку самі, використовуючи попередній метод, і намалювати їх одна за одною. Але це занадто складно і неефективно (за винятком випадків, коли це явно необхідно), тому ми просто малюємо лінії між кожною парою точок. Якщо радіус нашого опорного кола не великий, довжина кожної лінії між парою точок ніколи не буде достатньо довгою, щоб побачити її. Якби це сталося, нам би довелося збільшити кількість точок.
Малювання дуги на екрані¶
Тепер у нас є функція, яка малює щось на екрані; настав час викликати її всередині функції _draw():
func _draw():
var center = Vector2(200, 200)
var radius = 80
var angle_from = 75
var angle_to = 195
var color = Color(1.0, 0.0, 0.0)
draw_circle_arc(center, radius, angle_from, angle_to, color)
public override void _Draw()
{
var center = new Vector2(200, 200);
float radius = 80;
float angleFrom = 75;
float angleTo = 195;
var color = new Color(1, 0, 0);
DrawCircleArc(center, radius, angleFrom, angleTo, color);
}
Результат:
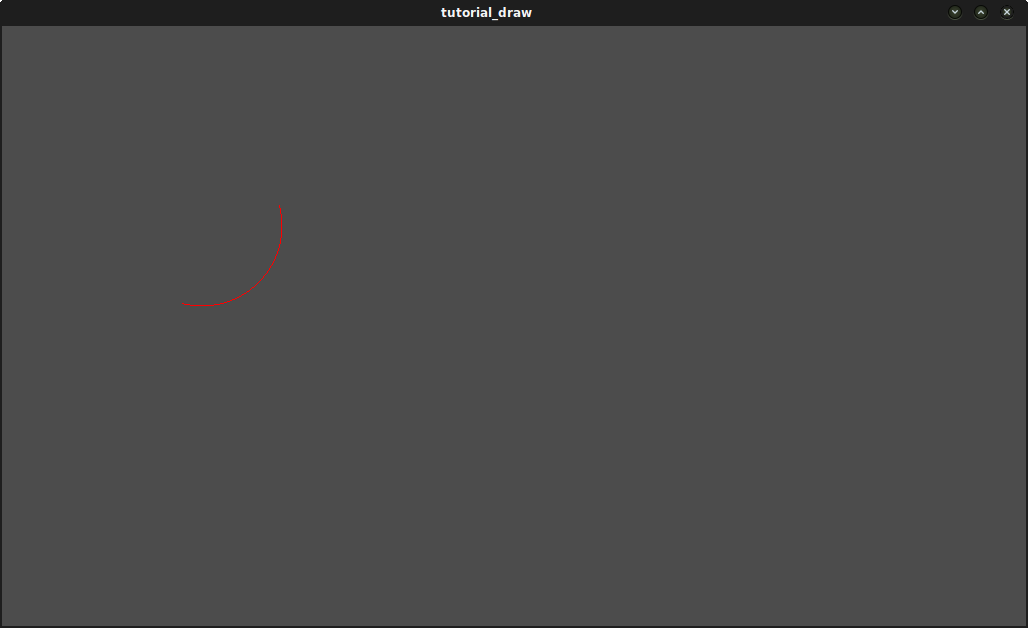
Функція полігона дуги¶
Ми можемо зробити ще крок далі і не тільки написати функцію, яка малює просту частину диска, визначену дугою, але і його форму. Метод точно такий же, як і раніше, за винятком того, що ми малюємо багатокутник замість ліній:
func draw_circle_arc_poly(center, radius, angle_from, angle_to, color):
var nb_points = 32
var points_arc = PackedVector2Array()
points_arc.push_back(center)
var colors = PackedColorArray([color])
for i in range(nb_points + 1):
var angle_point = deg_to_rad(angle_from + i * (angle_to - angle_from) / nb_points - 90)
points_arc.push_back(center + Vector2(cos(angle_point), sin(angle_point)) * radius)
draw_polygon(points_arc, colors)
public void DrawCircleArcPoly(Vector2 center, float radius, float angleFrom, float angleTo, Color color)
{
int nbPoints = 32;
var pointsArc = new Vector2[nbPoints + 2];
pointsArc[0] = center;
var colors = new Color[] { color };
for (int i = 0; i <= nbPoints; i++)
{
float anglePoint = Mathf.DegToRad(angleFrom + i * (angleTo - angleFrom) / nbPoints - 90);
pointsArc[i + 1] = center + new Vector2(Mathf.Cos(anglePoint), Mathf.Sin(anglePoint)) * radius;
}
DrawPolygon(pointsArc, colors);
}

Динаміка власного малювання¶
Гаразд, тепер ми можемо малювати власні речі на екрані. Однак малюнок статичний; давайте зробимо так, щоб ця форма обернулася по центру. Рішення полягає в тому, щоб просто змінити з плином часу значення angle_from і angle_to. Наприклад, ми просто збільшимо їх на 50. Це значення приросту має залишатися постійним, інакше швидкість обертання відповідно зміниться.
По-перше, ми повинні зробити як angle_from, так і angle_to глобальними змінними у верхній частині нашого скрипта. Також завбачте, що ви можете зберігати їх в інших вузлах і отримати до них доступ за допомогою get_node().
extends Node2D
var rotation_angle = 50
var angle_from = 75
var angle_to = 195
using Godot;
public partial class MyNode2D : Node2D
{
private float _rotationAngle = 50;
private float _angleFrom = 75;
private float _angleTo = 195;
}
Ми вносимо ці змінюючі значення в функції _process(delta).
Ми також збільшуємо тут наші змінні angle_from та angle_to. Однак не можна забувати про отримані значення від 0 до 360°! Тобто, якщо кут дорівнює 361°, то насправді це 1°. Якщо ви не обернете ці значення, скрипт буде працювати правильно, але кутові значення будуть рости все більше і більше з часом, поки не досягнуть максимального цілого значення, яким Godot може керувати (2^31 - 1). Коли це відбудеться, Godot може аварійно зазнати краху або викликати несподівану поведінку.
Finally, we must not forget to call the queue_redraw() function, which automatically
calls _draw(). This way, you can control when you want to refresh the frame.
func _process(delta):
angle_from += rotation_angle
angle_to += rotation_angle
# We only wrap angles when both of them are bigger than 360.
if angle_from > 360 and angle_to > 360:
angle_from = wrapf(angle_from, 0, 360)
angle_to = wrapf(angle_to, 0, 360)
queue_redraw()
public override void _Process(double delta)
{
_angleFrom += _rotationAngle;
_angleTo += _rotationAngle;
// We only wrap angles when both of them are bigger than 360.
if (_angleFrom > 360 && _angleTo > 360)
{
_angleFrom = Mathf.Wrap(_angleFrom, 0, 360);
_angleTo = Mathf.Wrap(_angleTo, 0, 360);
}
QueueRedraw();
}
Крім того, не забудьте змінити функцію _draw(), щоб використовувати ці змінні:
func _draw():
var center = Vector2(200, 200)
var radius = 80
var color = Color(1.0, 0.0, 0.0)
draw_circle_arc( center, radius, angle_from, angle_to, color )
public override void _Draw()
{
var center = new Vector2(200, 200);
float radius = 80;
var color = new Color(1, 0, 0);
DrawCircleArc(center, radius, _angleFrom, _angleTo, color);
}
Давайте запустимо! Це працює, але дуга обертається шалено швидко! Що не так?
Причина в тому, що ваш графічний процесор насправді відображає кадри так швидко, як може. Потрібно "нормалізувати" малюнок на цій швидкості; для цього ми повинні використовувати параметр delta функції _process(). delta містить час, що минув між двома останніми відтвореними кадрами. Як правило, він невеликий (близько 0,0003 секунд, але це залежить від вашого обладнання), тому використання delta для керування вимальовуванням гарантує, що ваша програма працюватиме з однаковою швидкістю на різному обладнанні.
У нашому випадку нам просто потрібно помножити нашу змінну rotation_angle на delta в функції _process(). Таким чином, наші 2 кути будуть збільшені на набагато менші значення, які безпосередньо залежить від швидкості рендеринга.
func _process(delta):
angle_from += rotation_angle * delta
angle_to += rotation_angle * delta
# We only wrap angles when both of them are bigger than 360.
if angle_from > 360 and angle_to > 360:
angle_from = wrapf(angle_from, 0, 360)
angle_to = wrapf(angle_to, 0, 360)
queue_redraw()
public override void _Process(double delta)
{
_angleFrom += _rotationAngle * (float)delta;
_angleTo += _rotationAngle * (float)delta;
// We only wrap angles when both of them are bigger than 360.
if (_angleFrom > 360 && _angleTo > 360)
{
_angleFrom = Wrap(_angleFrom, 0, 360);
_angleTo = Wrap(_angleTo, 0, 360);
}
QueueRedraw();
}
Давайте запустимо ще раз! На цей раз відображення обертання відбувається правильно!
Згладжування¶
Godot offers method parameters in draw_line
to enable antialiasing, but not all custom drawing methods offer this antialiased
parameter.
For custom drawing methods that don't provide an antialiased parameter,
you can enable 2D MSAA instead, which affects rendering in the entire viewport.
This provides high-quality antialiasing, but a higher performance cost and only
on specific elements. See 2D antialiasing for more information.
Інструменти¶
Малювання власних вузлів також може бути бажаним під час їх запуску в редакторі. Його можна використати в якості попереднього перегляду, або візуалізації певної функції, чи поведінки. Більше про це в Running code in the editor.