Up to date
This page is up to date for Godot 4.2.
If you still find outdated information, please open an issue.
Векторна математика¶
Вступ¶
Ця стаття — це короткий вступ до лінійної алгебри та опис способів її використання в розробці ігор. Лінійна алгебра — це наука про вектори та їх використання. Використовувати їх можна як в 2D, так і в 3D й Godot робить це дуже часто. Для того, щоб бути добрим програмістом, розуміти векторну математику просто необхідно.
Примітка
Ця стаття — це не підручник з лінійної алгебри. Ми лише розглянемо, як їх можна використовувати в прив'язці до розробки ігор. Для ширшого розуміння математики, погляньте на https://www.khanacademy.org/math/linear-algebra
Система координат (2D)¶
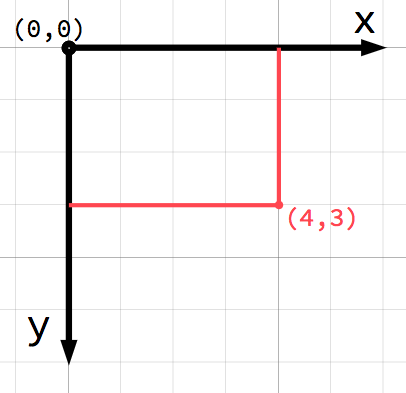
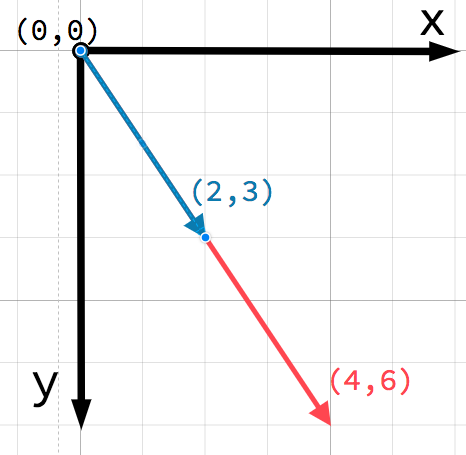
У двовимірному просторі, координати описуються за допомогою горизонтальної (x) та вертикальної (y) осей. Певна точка в просторі описується як пара чисел. Наприклад: (4,3).
Примітка
Якщо ви раніше не працювали з комп'ютерною графікою, то вам може здатись дивним, що вісь y напрямлена вниз а не вгору, як зазвичай, в підручниках з математики. Проте, такий підхід поширений серед більшости графічних комп'ютерних програм.
Будь-яка точка на площині може бути визначена як пара чисел у такий спосіб. А ще, ми можемо уявляти точку (4,3) як зміщення від точки (0,0), або початкової точки. Намалюймо стрілку, яка тягнеться від початкової точки до нашої:
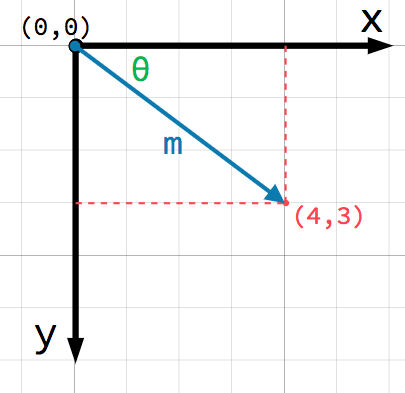
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
Варто зазначити, що вектор описує лише відносний напрямок та відносне зміщення. Вектори не мають такої штуки, як положення. Дві стрілки на зображенні нижче — це той самий вектор:
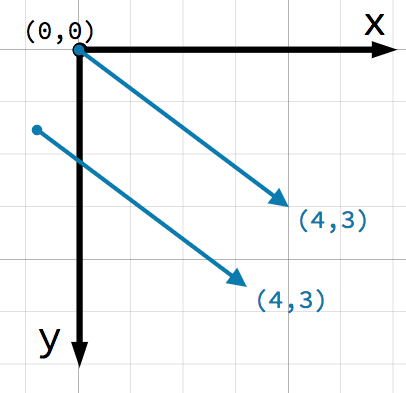
Обидва вектори позначають точку яка лежить на 4 одиниці вправо та на 3 одиниці вниз від деякої початкової точки. Не важливо де ви намалюєте вектор, він завжди буде позначати відносний напрямок та зміщення.
Дії над векторами¶
Ви можете описувати вектор як пару координат x та y, або як пару з кута й модуля. Але, зазвичай, програмісти використовують координатну форму. Наприклад, в Godot, початок координат знаходиться в верхньому лівому куті екрану. А тому, щоб розмістити 2D вузол під назвою Node2D на 400 пікселів правіше й на 300 пікселів нижче, потрібно використати такий код:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Godot supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
Доступ до компонентів¶
Окремі компоненти вектора можна отримати напряму, по назві.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Додавання векторів¶
Коли додаються або віднімаються два вектори, додаються і їхні відповідні компоненти:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
Суму векторів можна зобразити додавши один вектор, до кінця іншого:
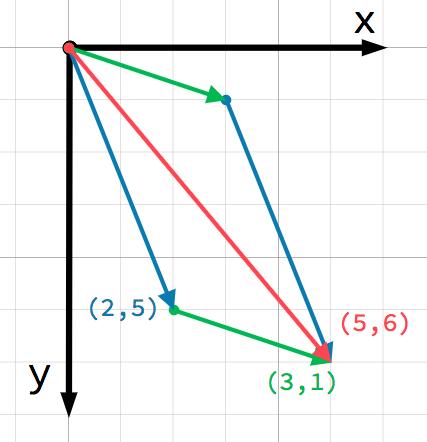
Сума a + b дає такий же результат як і b + a.
Множення на скаляр¶
Примітка
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Godot.
Вектор можна помножити на скаляр:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Примітка
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
Практичне застосування¶
Погляньмо на два найпоширеніші способи використання суми та різниці векторів.
Пересування¶
A vector can represent any quantity with a magnitude and direction. Typical
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
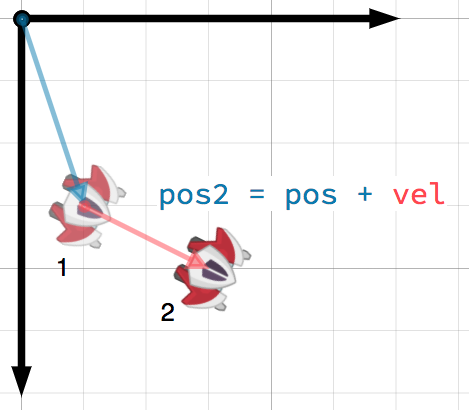
Порада
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
Указування на ціль¶
В цій ситуації, ви маєте танка, який хоче направити свою гармату на робота. Різниця положень танка й робота дасть нам вектор що вказує від танка, до робота.
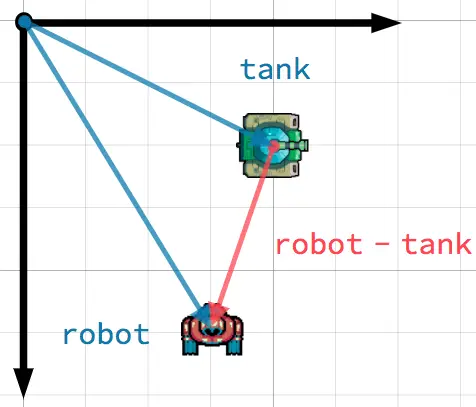
Порада
To find a vector pointing from A to B, use B - A.
Одиничні вектори¶
Вектор з довжиною 1 називається одиничним вектором. Їх ще іноді називають напрямними векторами чи нормалями. Одиничні вектори корисні, коли необхідно знати про напрямок без довжини.
Нормалізація¶
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Godot provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
Попередження
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
Відбиття¶
Вектори часто використовуються для того, щоб позначати нормалі. Вектор нормалі — це одиничний вектор, спрямований перпендикулярно до якоїсь поверхні. Він вказує на сторону, в яку повернута ця поверхня. Нормалі використовуються при обчисленні освітлення, зіткнень та інших операцій, зв'язаних із поверхнями.
Наприклад, уявімо, що ми маємо кулю, що рухається і ми хочемо, щоб вона відбилася від стіни чи іншого об'єкта:
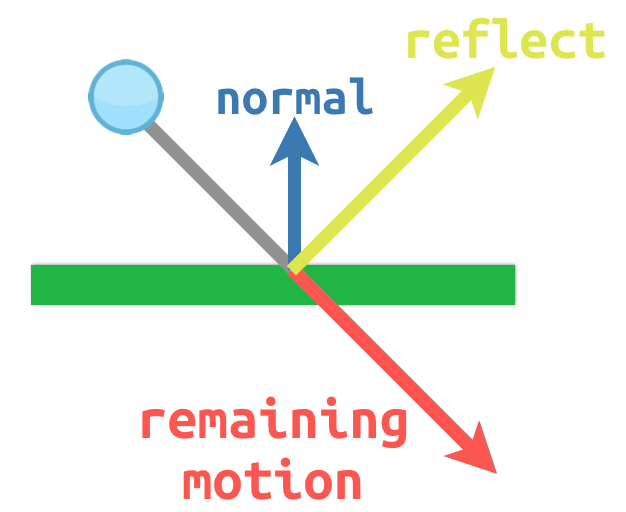
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Godot, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Скалярний добуток¶
Скалярний добуток — це одне з найважливіших понять у векторній математиці. Проте, його часто не розуміють. Скалярний добуток — це операція, яка бере два вектори, та повертає скаляр. На відміну від векторів, які мають модуль та напрямок, скаляр — це просто число, яке має лише модуль.
Є дві формули для обчислення скалярного добутку:
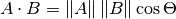
і
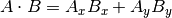
The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
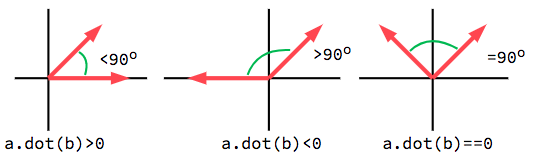
Якщо множаться одиничні вектори, то результат буде в межах від -1 (180°) до 1 (0°).
Напрямок¶
Ми можемо використати це для того, щоб дізнатись, чи дивиться один об'єкт на іншого. На схемі нижче, гравець p намагається уникати зомбі A і B. Припустімо, поле зору зомбі має кут 180°, чи можуть вони побачити гравця?
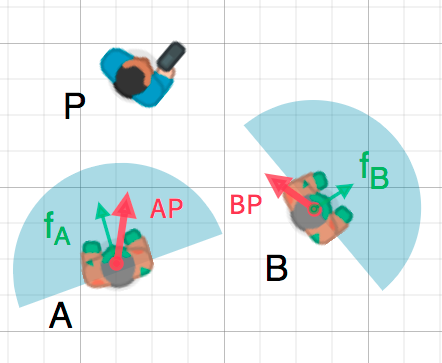
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Godot has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
У коді це виглядатиме ось так:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Векторний добуток¶
Як і скалярний добуток, векторний добуток — це операція над двома векторами. Але результат векторного добутку — це ще один вектор, який направлений перпендикулярно до двох інших. Його довжина залежить від кута між ними. Якщо вектори паралельні — то результатом векторного добутку буде нульовий вектор.

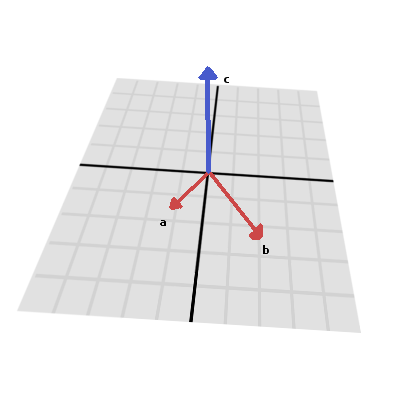
Ось так обчислюється векторний добуток:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Godot, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
Примітка
Для векторного добутку важливий порядок: a.cross(b) дасть інший результат аніж b.cross(a). Отримані вектори будуть дивитись у протилежні сторони.
Обчислення нормалей¶
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
Ось функція для обчислення нормалі трикутника:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Указування на ціль¶
У розділі про скалярний добуток ми побачили, як він може бути використаний для знаходження кута між векторами. Цього не достатньо для повороту в 3D. Нам також потрібно знати навколо якої осі обертатись. Ми можемо знайти її знайшовши векторний добуток між вектором який дивиться уперед і тим, що направлений на ціль. Отриманий перпендикуляр і буде віссю обертання.
Додаткова інформація¶
Дізнатись більше про використання векторів у Godot можна в наступних статтях: