Attention: Here be dragons

This is the latest (unstable) version of this documentation, which may document features not available in or compatible with released stable versions of Godot.

Checking the stable version of the documentation...

Безьє, криві і шляхи

Криві Безьє є математичним наближенням природних геометричних фігур. Ми використовуємо їх для представлення кривої з якомога меншою кількістю інформації та з високим рівнем гнучкості.

На відміну від більш абстрактних математичних понять, криві Безьє були створені для промислового дизайну. Вони є популярним інструментом в індустрії графічного програмного забезпечення.

Вони покладаються на інтерполяцію, яку ми бачили в попередній статті, поєднуючи кілька кроків для створення плавних кривих. Щоб краще зрозуміти, як працюють криві Безьє, почнемо з її найпростішої форми: Квадратична Безьє.

Квадратична крива Безьє

Візьміть три точки, це мінімум, необхідний для роботи Квадратичної Безьє:

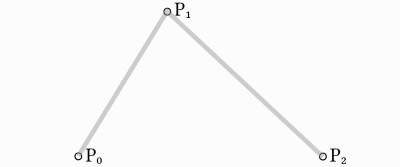
../../_images/bezier_quadratic_points.png

Щоб намалювати криву між ними, ми спочатку поступово інтерполюємо дві вершини кожного з двох відрізків, утворених трьома точками, використовуючи значення в діапазоні від 0 до 1. Це дає нам дві точки, які рухаються вздовж сегментів, коли ми змінюємо значення t від 0 до 1.

func _quadratic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, t: float):
    var q0 = p0.lerp(p1, t)
    var q1 = p1.lerp(p2, t)

private Vector2 QuadraticBezier(Vector2 p0, Vector2 p1, Vector2 p2, float t)
{
    Vector2 q0 = p0.Lerp(p1, t);
    Vector2 q1 = p1.Lerp(p2, t);
}

Потім ми інтерполюємо q0 і q1, щоб отримати одну точку r, яка рухається вздовж кривої.

var r = q0.lerp(q1, t)
return r

Vector2 r = q0.Lerp(q1, t);
return r;

Цей тип кривої називається Квадратичною кривою Безьє.

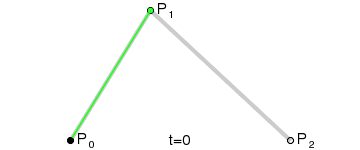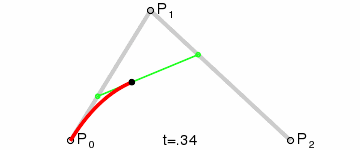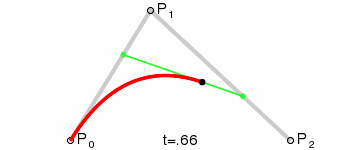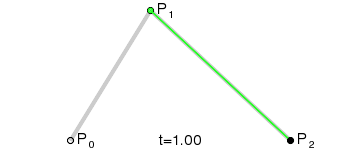
../../_images/bezier_quadratic_points2.gif

(Зображення запозичене з Вікіпедії)

Кубічна крива Безьє

Опираючись на попередній приклад, ми можемо отримати більше контролю, за допомогою інтерполяції між чотирма точками.

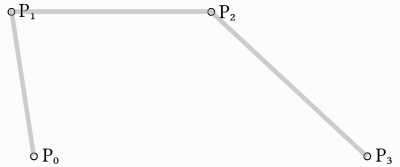
Спочатку ми використовуємо функцію з чотирма параметрами, щоб взяти чотири точки p0, p1, p2 та p3:

func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):

public Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{

}

Застосовуємо лінійну інтерполяцію до кожної пари точок, щоб зменшити їх до трьох:

var q0 = p0.lerp(p1, t)
var q1 = p1.lerp(p2, t)
var q2 = p2.lerp(p3, t)

Vector2 q0 = p0.Lerp(p1, t);
Vector2 q1 = p1.Lerp(p2, t);
Vector2 q2 = p2.Lerp(p3, t);

Потім беремо наші три точки і зменшуємо їх до двох:

var r0 = q0.lerp(q1, t)
var r1 = q1.lerp(q2, t)

Vector2 r0 = q0.Lerp(q1, t);
Vector2 r1 = q1.Lerp(q2, t);

І до одної:

var s = r0.lerp(r1, t)
return s

Vector2 s = r0.Lerp(r1, t);
return s;

Ось повна функція:

func _cubic_bezier(p0: Vector2, p1: Vector2, p2: Vector2, p3: Vector2, t: float):
    var q0 = p0.lerp(p1, t)
    var q1 = p1.lerp(p2, t)
    var q2 = p2.lerp(p3, t)

    var r0 = q0.lerp(q1, t)
    var r1 = q1.lerp(q2, t)

    var s = r0.lerp(r1, t)
    return s

private Vector2 CubicBezier(Vector2 p0, Vector2 p1, Vector2 p2, Vector2 p3, float t)
{
    Vector2 q0 = p0.Lerp(p1, t);
    Vector2 q1 = p1.Lerp(p2, t);
    Vector2 q2 = p2.Lerp(p3, t);

    Vector2 r0 = q0.Lerp(q1, t);
    Vector2 r1 = q1.Lerp(q2, t);

    Vector2 s = r0.Lerp(r1, t);
    return s;
}

Результатом буде плавна крива інтерполяції між усіма чотирма точками:

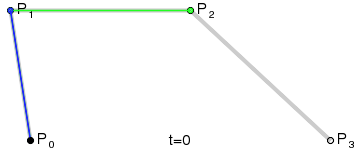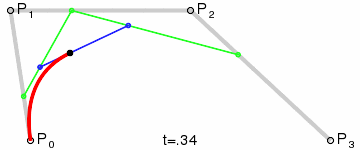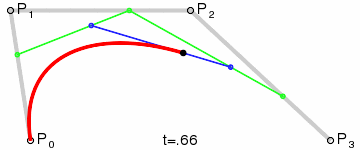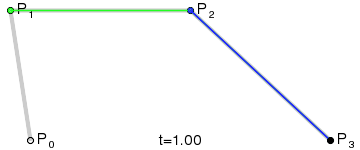
(Зображення запозичене з Вікіпедії)

Примітка

Кубічна інтерполяція Безьє працює так само в 3D, просто використовуйте Vector3 замість Vector2.

Додавання контрольних точок

Спираючись на Кубічну Безьє, ми можемо змінити спосіб роботи двох точок, щоб вільно контролювати форму нашої кривої. Замість того, щоб мати p0, p1, p2 та p3, ми будемо зберігати їх як:

point0 = p0: Перша точка, джерело
control0 = p1 - p0: Це вектор відносно першої контрольної точки
control1 = p3 - p2: Це вектор відносно другої контрольної точки
point1 = p3: Це друга точка, пункт призначення

Таким чином, ми маємо дві точки і дві контрольні точки, які є відносними векторами до відповідних точок. Якщо ви раніше використовували графічне, або анімаційне, програмне забезпечення, це може виглядати знайомим:

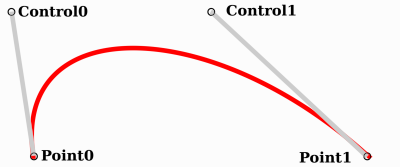
Ось як графічне програмне забезпечення представляє користувачам криві Безьє, і як вони працюють і виглядають в Godot.

Curve2D, Curve3D, Path та Path2D

Є два об'єкти, які містять криві: Curve3D та Curve2D (для 3D і 2D відповідно).

Вони можуть містити кілька точок, дозволяючи довші шляхи. Також можна встановити їх на вузли: Path3D і Path2D (також для 3D і 2D відповідно):

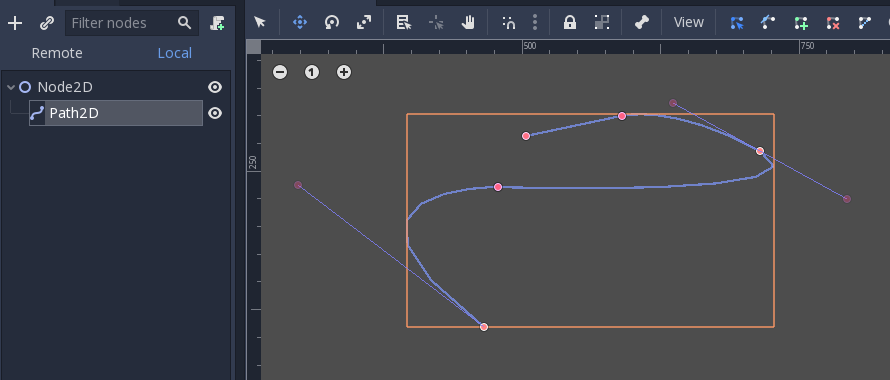
Використання їх, однак, може бути не зовсім очевидним, тому нижче наведено опис найбільш поширених випадків використання кривих Безьє.

Оцінювання

Лише їх оцінка може бути варіантом, але в більшості випадків це не дуже корисно. Великим недоліком кривих Без’є є те, що якщо ви перетинаєте їх із постійною швидкістю, від t = 0 до t = 1, фактична інтерполяція не рухатиметься з постійною швидкістю. Швидкість також є інтерполяцією між відстанями між точками p0, p1, p2 і p3, і не існує математично простого способу проходження кривої з постійною швидкістю.

Розглянемо приклад із таким псевдокодом:

var t = 0.0

func _process(delta):
    t += delta
    position = _cubic_bezier(p0, p1, p2, p3, t)

private float _t = 0.0f;

public override void _Process(double delta)
{
    _t += (float)delta;
    Position = CubicBezier(p0, p1, p2, p3, _t);
}

../../_images/bezier_interpolation_speed.gif

Як бачите, швидкість (в пікселях в секунду) кола варіюється, хоча t і збільшується з постійною швидкістю. Це ускладнює використання безьє для якихось практичних нестандартних речей.

Малюнок

Малювання кривими Безьє (або об'єктів на їх основі) є дуже поширеним випадком використання, але це також непросто. Майже в будь-якому випадку криві Безьє повинні бути перетворені в якісь сегменти. Це, як правило, важко, без створення їх дуже великої кількості.

Причина в тому, що деякі ділянки кривої (зокрема, кути) можуть зажадати значної кількості точок, в той час як інші ні:

Крім того, якби обидві контрольні точки були 0, 0 (пам'ятайте, що вони є відносними векторами), крива Безьє була б просто прямою лінією (тому малювання великої кількості точок було б марним).

Перед малюванням кривих Безьє потрібно виконати тесселяцію. Це часто робиться за допомогою рекурсивної, або поділяючої і підпорядковуючої, функції, яка розділяє криву, поки величина кривизни не стане меншою за певний поріг.

Класи кривих Curve забезпечують це за допомогою функції Curve2D.tessellate() (яка отримує необов'язкові аргументи рекурсії stages та кута tolerance). Таким чином, намалювати щось на основі кривої стає простіше.

Обхід

Останній поширений випадок використання кривих - це їх обхід. Через, згадувану раніше, постійну швидкість, це також важко.

Щоб зробити це легше, криві потрібно запікати в рівновіддалених точках. Таким чином, їх можна апроксимувати за допомогою звичайної інтерполяції (яку можна додатково вдосконалити за допомогою кубічної опції). Для цього просто використовуйте метод Curve3D.sample_baked() разом із Curve2D.get_baked_length(). Перший виклик будь-якого з них призведе до внутрішньої обробки кривої.

Таким чином, обхід із постійною швидкістю можна виконати за допомогою такого псевдокоду:

var t = 0.0

func _process(delta):
    t += delta
    position = curve.sample_baked(t * curve.get_baked_length(), true)

private float _t = 0.0f;

public override void _Process(double delta)
{
    _t += (float)delta;
    Position = curve.SampleBaked(_t * curve.GetBakedLength(), true);
}

І в результаті отримаємо рух з постійною швидкістю: